分块策略详解

文档拆分策略有多种，每种策略都有其自身的优势。

但是粗略来说我们1~5的分块策略是由差到好的，具体可以根据项目多方面测试下

1. 固定长度拆分（简单粗暴）

最直观的策略是根据固定长度进行拆分。

就像用刀切面包一样，每100个字符就切一刀，不管切到哪里。

from langchain_text_splitters import CharacterTextSplitter
text_splitter = CharacterTextSplitter(chunk_size=100, chunk_overlap=0, separator="")

document="""One of the most important things I didn't understand about the world when I was a child is the degree to which the returns for performance are superlinear.

Teachers and coaches implicitly told us the returns were linear. "You get out," I heard a thousand times, "what you put in." They meant well, but this is rarely true. If your product is only half as good as your competitor's, you don't get half as many customers. You get no customers, and you go out of business.

It's obviously true that the returns for performance are superlinear in business. Some think this is a flaw of capitalism, and that if we changed the rules it would stop being true. But superlinear returns for performance are a feature of the world, not an artifact of rules we've invented. We see the same pattern in fame, power, military victories, knowledge, and even benefit to humanity. In all of these, the rich get richer. [1]

You can't understand the world without understanding the concept of superlinear returns. And if you're ambitious you definitely should, because this will be the wave you surf on.

It may seem as if there are a lot of different situations with superlinear returns, but as far as I can tell they reduce to two fundamental causes: exponential growth and thresholds.

The most obvious case of superlinear returns is when you're working on something that grows exponentially. For example, growing bacterial cultures. When they grow at all, they grow exponentially. But they're tricky to grow. Which means the difference in outcome between someone who's adept at it and someone who's not is very great.

Startups can also grow exponentially, and we see the same pattern there. Some manage to achieve high growth rates. Most don't. And as a result you get qualitatively different outcomes: the companies with high growth rates tend to become immensely valuable, while the ones with lower growth rates may not even survive.

Y Combinator encourages founders to focus on growth rate rather than absolute numbers. It prevents them from being discouraged early on, when the absolute numbers are still low. It also helps them decide what to focus on: you can use growth rate as a compass to tell you how to evolve the company. But the main advantage is that by focusing on growth rate you tend to get something that grows exponentially.

YC doesn't explicitly tell founders that with growth rate "you get out what you put in," but it's not far from the truth. And if growth rate were proportional to performance, then the reward for performance p over time t would be proportional to pt.

Even after decades of thinking about this, I find that sentence startling."""
texts = text_splitter.split_text(document)
total_characters = len(document)
num_chunks = len(texts)
average_chunk_size = total_characters/len(texts)

print(f"Total Characters: {total_characters}")
print(f"Number of chunks: {num_chunks}")
print(f"Average chunk size: {average_chunk_size:.1f}")
print(f"\nFirst few chunks:")
for i, chunk in enumerate(texts[:3]):
    print(f"Chunk {i+1} ({len(chunk)} chars): {chunk[:100]}...")

控制台会输出：

以上结果我们可以在https://chunkviz.up.railway.app/ 看到，如下图：

一般实战中我们会设置约10%-20%做重叠窗口，这样可以使得模型分块之后可以具备连续上下文逻辑。

2. 递归字符拆分（智能切割）

最直观的策略是根据固定长度进行拆分。这种简单而有效的方法可以确保每个块不超过指定的大小限制。

就像用刀切面包一样，每100个字符就切一刀，不管切到哪里。

1. 首先尝试按最大单位切割（段落）

# 就像先按整个萝卜来分
段落1 = "这是第一段内容..."
段落2 = "这是第二段内容..." 
段落3 = "这是第三段内容..."

2. 如果段落太大，就切成句子

# 萝卜太大了，按句子切
句子1 = "这是第一个句子。"
句子2 = "这是第二个句子。"
句子3 = "这是第三个句子。"

3. 如果句子还是太大，就切成单词

# 句子还是太长，按单词切
单词1 = "这是"
单词2 = "第一个"
单词3 = "很长的"
单词4 = "句子"

4. 最后实在没办法，才按字符切

# 实在没办法了，按字符切
字符1 = "这"
字符2 = "是"
字符3 = "一"
字符4 = "个"

from langchain_text_splitters import RecursiveCharacterTextSplitter
text_splitter = RecursiveCharacterTextSplitter(chunk_size=100, chunk_overlap=0)

document="""One of the most important things I didn't understand about the world when I was a child is the degree to which the returns for performance are superlinear.

Teachers and coaches implicitly told us the returns were linear. "You get out," I heard a thousand times, "what you put in." They meant well, but this is rarely true. If your product is only half as good as your competitor's, you don't get half as many customers. You get no customers, and you go out of business.

It's obviously true that the returns for performance are superlinear in business. Some think this is a flaw of capitalism, and that if we changed the rules it would stop being true. But superlinear returns for performance are a feature of the world, not an artifact of rules we've invented. We see the same pattern in fame, power, military victories, knowledge, and even benefit to humanity. In all of these, the rich get richer. [1]

You can't understand the world without understanding the concept of superlinear returns. And if you're ambitious you definitely should, because this will be the wave you surf on.

It may seem as if there are a lot of different situations with superlinear returns, but as far as I can tell they reduce to two fundamental causes: exponential growth and thresholds.

The most obvious case of superlinear returns is when you're working on something that grows exponentially. For example, growing bacterial cultures. When they grow at all, they grow exponentially. But they're tricky to grow. Which means the difference in outcome between someone who's adept at it and someone who's not is very great.

Startups can also grow exponentially, and we see the same pattern there. Some manage to achieve high growth rates. Most don't. And as a result you get qualitatively different outcomes: the companies with high growth rates tend to become immensely valuable, while the ones with lower growth rates may not even survive.

Y Combinator encourages founders to focus on growth rate rather than absolute numbers. It prevents them from being discouraged early on, when the absolute numbers are still low. It also helps them decide what to focus on: you can use growth rate as a compass to tell you how to evolve the company. But the main advantage is that by focusing on growth rate you tend to get something that grows exponentially.

YC doesn't explicitly tell founders that with growth rate "you get out what you put in," but it's not far from the truth. And if growth rate were proportional to performance, then the reward for performance p over time t would be proportional to pt.

Even after decades of thinking about this, I find that sentence startling."""

texts = text_splitter.split_text(document)
total_characters = len(document)
num_chunks = len(texts)
average_chunk_size = total_characters/len(texts)

print(f"Total Characters: {total_characters}")
print(f"Number of chunks: {num_chunks}")
print(f"Average chunk size: {average_chunk_size:.1f}")
print(f"\nFirst few chunks:")
for i, chunk in enumerate(texts[:3]):
    print(f"Chunk {i+1} ({len(chunk)}字符): {chunk}")

控制台会输出：

以上结果我们可以在https://chunkviz.up.railway.app/ 看到，如下图：

这个网站开发者将空格也视为了分割块，可忽略它的span数计算总数与我们不一样（它的bug）：

该方法是dify的默认方法。我们可以修改分割符从而快速简单达到效果，比如
separators 分隔符设置：
默认的separators 是"\n\n"（即回车）。比如：

• 中文文档：应增加中文标点符号（如"。“、”，"）作为分隔符
• Markdown文档：可使用标题标记（#、##）、代码块标记（```）等作为分隔符

3. 特殊格式拆分（定向打击）

某些文档具有固有的结构，例如 HTML、Markdown 或 JSON 文件。
这里我就先介绍下Markdown ，其他我遇到了再跟大家补充。

Markdown分块

MarkdownHeaderTextSplitter是对RecursiveCharacterTextSplitter用了多个不同符号使得其能适应格式。
包含了以下符号作为分隔符：

• # 到 ######

• ````lang` - 三个反引号开始的代码块

• ~~~lang - 三个波浪号开始的代码块

• *** - 星号分割线（3个或更多）

• --- - 短横线分割线（3个或更多）

• ___ - 下划线分割线（3个或更多）

4. 语义分割（更智能切割）

递归文本分块基于预定义规则工作，虽然简单高效，但可能无法准确捕捉语义变化。
基于语义的分块策略则直接分析文本内容，根据语义相似度判断分块位置。

基于Embedding的语义分块

但从概念上讲，该方法是在文本含义发生显著变化时对文本进行拆分。例如，我们可以使用滑动窗口方法生成嵌入向量，并比较嵌入以发现显著差异：

1. 句子分割 首先将整个文本按句子分割（默认按句号、问号、感叹号分割）。

2. 创建语义窗口 为了获得更稳定的语义表示，不是单独分析每个句子，而是创建"滑动窗口"。默认情况下，每个窗口包含3个句子：当前句子加上前后各一个句子。这样做可以减少单个短句造成的噪音。

3. 生成嵌入向量 对每个滑动窗口的组合句子生成嵌入向量，这些向量能够捕获文本的语义含义。

4. 计算语义距离 计算相邻窗口之间的余弦距离。余弦距离越大，说明两个窗口的语义差异越大。

5. 确定断点阈值 系统提供4种方法来确定什么程度的语义距离算作"断点"：

• 百分位数法：找出距离最大的前5%作为断点
• 标准差法：超过平均值加3倍标准差的距离作为断点
• 四分位数法：基于四分位距离的统计方法
• 梯度法：分析距离变化的梯度来找断点

6. 执行分割 在语义距离超过阈值的位置进行分割，形成最终的语义块。

from langchain_experimental.text_splitter import SemanticChunker
from langchain_community.embeddings import HuggingFaceBgeEmbeddings
import os
os.environ['HF_ENDPOINT'] = 'https://hf-mirror.com'

model_name = "BAAI/bge-small-en"
model_kwargs = {"device": "cpu"}
encode_kwargs = {"normalize_embeddings": True}
hf = HuggingFaceBgeEmbeddings(
    model_name=model_name, model_kwargs=model_kwargs, encode_kwargs=encode_kwargs
)

text_splitter = SemanticChunker(hf)
document="""One of the most important things I didn't understand about the world when I was a child is the degree to which the returns for performance are superlinear.

Teachers and coaches implicitly told us the returns were linear. "You get out," I heard a thousand times, "what you put in." They meant well, but this is rarely true. If your product is only half as good as your competitor's, you don't get half as many customers. You get no customers, and you go out of business.

It's obviously true that the returns for performance are superlinear in business. Some think this is a flaw of capitalism, and that if we changed the rules it would stop being true. But superlinear returns for performance are a feature of the world, not an artifact of rules we've invented. We see the same pattern in fame, power, military victories, knowledge, and even benefit to humanity. In all of these, the rich get richer. [1]

You can't understand the world without understanding the concept of superlinear returns. And if you're ambitious you definitely should, because this will be the wave you surf on.

It may seem as if there are a lot of different situations with superlinear returns, but as far as I can tell they reduce to two fundamental causes: exponential growth and thresholds.

The most obvious case of superlinear returns is when you're working on something that grows exponentially. For example, growing bacterial cultures. When they grow at all, they grow exponentially. But they're tricky to grow. Which means the difference in outcome between someone who's adept at it and someone who's not is very great.

Startups can also grow exponentially, and we see the same pattern there. Some manage to achieve high growth rates. Most don't. And as a result you get qualitatively different outcomes: the companies with high growth rates tend to become immensely valuable, while the ones with lower growth rates may not even survive.

Y Combinator encourages founders to focus on growth rate rather than absolute numbers. It prevents them from being discouraged early on, when the absolute numbers are still low. It also helps them decide what to focus on: you can use growth rate as a compass to tell you how to evolve the company. But the main advantage is that by focusing on growth rate you tend to get something that grows exponentially.

YC doesn't explicitly tell founders that with growth rate "you get out what you put in," but it's not far from the truth. And if growth rate were proportional to performance, then the reward for performance p over time t would be proportional to pt.

Even after decades of thinking about this, I find that sentence startling."""
texts = text_splitter.create_documents([document])
print(texts[0].page_content)
print(len(texts))

total_characters = len(document)
num_chunks = len(texts)
average_chunk_size = total_characters/len(texts)

print(f"Total Characters: {total_characters}")
print(f"Number of chunks: {num_chunks}")
print(f"Average chunk size: {average_chunk_size:.1f}")
print(f"\nFirst few chunks:")
for i, chunk in enumerate(texts[:3]):
    print(f"Chunk {i+1}: {chunk}\n")

由于文本是英文的，可能我们还是不太能直观看明白Embedding模型做了什么，由此我又写了以下代码，这个代码将会从语义分割的实现到绘制图（工程上用上面那份代码即可，这份代码只是做解释）

from langchain_experimental.text_splitter import SemanticChunker
from langchain_community.embeddings import HuggingFaceBgeEmbeddings
import os
import re
import numpy as np
import matplotlib.pyplot as plt
from langchain_community.utils.math import cosine_similarity

# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 设置环境
os.environ['HF_ENDPOINT'] = 'https://hf-mirror.com'

# 初始化嵌入模型
model_name = "BAAI/bge-small-en"
model_kwargs = {"device": "cpu"}
encode_kwargs = {"normalize_embeddings": True}
hf = HuggingFaceBgeEmbeddings(
    model_name=model_name,
    model_kwargs=model_kwargs,
    encode_kwargs=encode_kwargs
)

# 你的文档内容
document = """One of the most important things I didn't understand about the world when I was a child is the degree to which the returns for performance are superlinear.

Teachers and coaches implicitly told us the returns were linear. "You get out," I heard a thousand times, "what you put in." They meant well, but this is rarely true. If your product is only half as good as your competitor's, you don't get half as many customers. You get no customers, and you go out of business.

It's obviously true that the returns for performance are superlinear in business. Some think this is a flaw of capitalism, and that if we changed the rules it would stop being true. But superlinear returns for performance are a feature of the world, not an artifact of rules we've invented. We see the same pattern in fame, power, military victories, knowledge, and even benefit to humanity. In all of these, the rich get richer. [1]

You can't understand the world without understanding the concept of superlinear returns. And if you're ambitious you definitely should, because this will be the wave you surf on.

It may seem as if there are a lot of different situations with superlinear returns, but as far as I can tell they reduce to two fundamental causes: exponential growth and thresholds.

The most obvious case of superlinear returns is when you're working on something that grows exponentially. For example, growing bacterial cultures. When they grow at all, they grow exponentially. But they're tricky to grow. Which means the difference in outcome between someone who's adept at it and someone who's not is very great.

Startups can also grow exponentially, and we see the same pattern there. Some manage to achieve high growth rates. Most don't. And as a result you get qualitatively different outcomes: the companies with high growth rates tend to become immensely valuable, while the ones with lower growth rates may not even survive.

Y Combinator encourages founders to focus on growth rate rather than absolute numbers. It prevents them from being discouraged early on, when the absolute numbers are still low. It also helps them decide what to focus on: you can use growth rate as a compass to tell you how to evolve the company. But the main advantage is that by focusing on growth rate you tend to get something that grows exponentially.

YC doesn't explicitly tell founders that with growth rate "you get out what you put in," but it's not far from the truth. And if growth rate were proportional to performance, then the reward for performance p over time t would be proportional to pt.

Even after decades of thinking about this, I find that sentence startling."""


def combine_sentences(sentences, buffer_size=1):
    """组合句子，创建滑动窗口"""
    for i in range(len(sentences)):
        combined_sentence = ""

        # 添加前面的句子
        for j in range(i - buffer_size, i):
            if j >= 0:
                combined_sentence += sentences[j]["sentence"] + " "

        # 添加当前句子
        combined_sentence += sentences[i]["sentence"]

        # 添加后面的句子
        for j in range(i + 1, i + 1 + buffer_size):
            if j < len(sentences):
                combined_sentence += " " + sentences[j]["sentence"]

        sentences[i]["combined_sentence"] = combined_sentence

    return sentences


def calculate_cosine_distances(sentences):
    """计算余弦距离"""
    distances = []
    for i in range(len(sentences) - 1):
        embedding_current = sentences[i]["combined_sentence_embedding"]
        embedding_next = sentences[i + 1]["combined_sentence_embedding"]

        # 计算余弦相似度
        similarity = cosine_similarity([embedding_current], [embedding_next])[0][0]

        # 转换为余弦距离
        distance = 1 - similarity
        distances.append(distance)
        sentences[i]["distance_to_next"] = distance

    return distances, sentences


# 手动实现语义距离计算
def calculate_semantic_distances(text, embeddings_model, buffer_size=1):
    """计算文本的语义距离"""
    # 按句子分割
    sentence_split_regex = r"(?<=[.?!])\s+"
    single_sentences_list = re.split(sentence_split_regex, text)
    single_sentences_list = [s.strip() for s in single_sentences_list if s.strip()]

    print(f"分割出 {len(single_sentences_list)} 个句子:")
    for i, sentence in enumerate(single_sentences_list):
        print(f"{i + 1}. {sentence[:100]}...")
    print()

    # 创建句子字典
    sentences = [{"sentence": x, "index": i} for i, x in enumerate(single_sentences_list)]

    # 组合句子（滑动窗口）
    sentences = combine_sentences(sentences, buffer_size)

    # 获取嵌入向量
    print("生成嵌入向量...")
    embeddings = embeddings_model.embed_documents([x["combined_sentence"] for x in sentences])

    for i, sentence in enumerate(sentences):
        sentence["combined_sentence_embedding"] = embeddings[i]

    # 计算距离
    distances, sentences = calculate_cosine_distances(sentences)

    return distances, sentences, single_sentences_list


# 计算语义距离
print("开始计算语义距离...")
distances, sentences_with_embeddings, original_sentences = calculate_semantic_distances(document, hf)

print(f"计算出 {len(distances)} 个距离值")
print("距离值:", [f"{d:.3f}" for d in distances])
print()

# 绘制图表
plt.figure(figsize=(15, 8))

# 绘制距离线
plt.plot(distances, linewidth=2, marker='o', markersize=4)

# 设置y轴上限
y_upper_bound = max(distances) * 1.2
plt.ylim(0, y_upper_bound)
plt.xlim(0, len(distances))

# 计算阈值
breakpoint_percentile_threshold = 95
breakpoint_distance_threshold = np.percentile(distances, breakpoint_percentile_threshold)

print(f"95%分位数阈值: {breakpoint_distance_threshold:.3f}")

# 绘制阈值线
plt.axhline(y=breakpoint_distance_threshold, color='r', linestyle='-', linewidth=2,
            label=f'95%阈值: {breakpoint_distance_threshold:.3f}')

# 计算超过阈值的距离数量
num_distances_above_threshold = len([x for x in distances if x > breakpoint_distance_threshold])
num_chunks = num_distances_above_threshold + 1

print(f"超过阈值的距离数量: {num_distances_above_threshold}")
print(f"最终块数: {num_chunks}")

# 显示块数量
plt.text(x=(len(distances) * 0.01), y=y_upper_bound * 0.9, s=f"{num_chunks} 个分块",
         fontsize=14, bbox=dict(boxstyle="round,pad=0.3", facecolor="yellow", alpha=0.7))

# 获取超过阈值的索引
indices_above_thresh = [i for i, x in enumerate(distances) if x > breakpoint_distance_threshold]
print(f"断点位置: {indices_above_thresh}")

# 为每个块着色和标注
colors = ['lightblue', 'lightgreen', 'lightcoral', 'lightyellow', 'lightpink', 'lightgray', 'lightcyan']

# 处理第一个块
if indices_above_thresh:
    # 第一个块：从开始到第一个断点
    plt.axvspan(0, indices_above_thresh[0], facecolor=colors[0], alpha=0.3)
    plt.text(x=indices_above_thresh[0] / 2,
             y=breakpoint_distance_threshold + y_upper_bound / 20,
             s=f"块 1", horizontalalignment='center', fontsize=10,
             bbox=dict(boxstyle="round,pad=0.2", facecolor=colors[0], alpha=0.8))

    # 中间的块
    for i in range(1, len(indices_above_thresh)):
        start_idx = indices_above_thresh[i - 1]
        end_idx = indices_above_thresh[i]
        plt.axvspan(start_idx, end_idx, facecolor=colors[i % len(colors)], alpha=0.3)
        plt.text(x=(start_idx + end_idx) / 2,
                 y=breakpoint_distance_threshold + y_upper_bound / 20,
                 s=f"块 {i + 1}", horizontalalignment='center', fontsize=10,
                 bbox=dict(boxstyle="round,pad=0.2", facecolor=colors[i % len(colors)], alpha=0.8))

    # 最后一个块：从最后一个断点到结束
    last_breakpoint = indices_above_thresh[-1]
    plt.axvspan(last_breakpoint, len(distances),
                facecolor=colors[len(indices_above_thresh) % len(colors)], alpha=0.3)
    plt.text(x=(last_breakpoint + len(distances)) / 2,
             y=breakpoint_distance_threshold + y_upper_bound / 20,
             s=f"块 {len(indices_above_thresh) + 1}", horizontalalignment='center', fontsize=10,
             bbox=dict(boxstyle="round,pad=0.2",
                       facecolor=colors[len(indices_above_thresh) % len(colors)], alpha=0.8))
else:
    # 如果没有断点，整个文档就是一块
    plt.axvspan(0, len(distances), facecolor=colors[0], alpha=0.3)
    plt.text(x=len(distances) / 2,
             y=y_upper_bound / 2,
             s="块 1", horizontalalignment='center', fontsize=12,
             bbox=dict(boxstyle="round,pad=0.3", facecolor=colors[0], alpha=0.8))

# 标记超过阈值的点
for i, distance in enumerate(distances):
    if distance > breakpoint_distance_threshold:
        plt.plot(i, distance, 'ro', markersize=8, markerfacecolor='red', markeredgecolor='darkred', markeredgewidth=2)
        plt.annotate(f'断点\n{distance:.3f}',
                     xy=(i, distance),
                     xytext=(i, distance + y_upper_bound / 10),
                     arrowprops=dict(arrowstyle='->', color='red', lw=1.5),
                     ha='center', fontsize=9,
                     bbox=dict(boxstyle="round,pad=0.2", facecolor="red", alpha=0.7, edgecolor="darkred"))

plt.title("超线性回报文章的语义距离分析", fontsize=16, fontweight='bold')
plt.xlabel("句子位置索引", fontsize=12)
plt.ylabel("连续句子间的余弦距离", fontsize=12)
plt.grid(True, alpha=0.3)
plt.legend()

# 添加距离统计信息
stats_text = f"""距离统计:
最小值: {min(distances):.3f}
最大值: {max(distances):.3f}
平均值: {np.mean(distances):.3f}
标准差: {np.std(distances):.3f}"""

plt.text(x=len(distances) * 0.7, y=y_upper_bound * 0.7, s=stats_text,
         fontsize=10, bbox=dict(boxstyle="round,pad=0.5", facecolor="white", alpha=0.8, edgecolor="gray"))

plt.tight_layout()
plt.show()

# 使用SemanticChunker进行实际分割验证
print("\n" + "=" * 50)
print("使用SemanticChunker验证结果:")
text_splitter = SemanticChunker(hf)
chunks = text_splitter.split_text(document)

print(f"SemanticChunker分割结果: {len(chunks)} 个块")
for i, chunk in enumerate(chunks):
    print(f"\n块 {i + 1} ({len(chunk)} 字符):")
    print(chunk[:200] + "..." if len(chunk) > 200 else chunk)

print(f"\n总字符数: {len(document)}")
print(f"平均块大小: {len(document) / len(chunks):.1f} 字符")

控制台输出为如下。

1. 句子分割 ✅
   首先按标点符号（句号、问号、感叹号）拆分文本，得到了29个独立句子。

2. 创建滑动窗口 (buffer_size=1) ✅
   为每个句子添加上下文，构建包含前后邻句的组合文本：

   • 句子1：只包含句子1+句子2（没有前句）
   • 句子2：包含句子1+句子2+句子3
   • 句子3：包含句子2+句子3+句子4
   • …
   • 句子29：只包含句子28+句子29（没有后句）

3. 生成嵌入向量
   使用BGE模型为29个组合句子生成768维的向量表示，每个向量捕获了句子及其上下文的语义信息。

4. 计算余弦距离
   计算相邻句子间的语义距离，得到28个距离值（两两之间计算29句就会变为28个距离）：

   • 距离值范围：0.011 到 0.096
   • 距离越大表示语义跳跃越明显

5. 确定分块阈值
   使用95%分位数作为分块阈值：

   • 计算所有距离的95%分位数
   • 超过这个阈值的位置被认为是语义断点

6. 识别分块点
   找出距离值超过阈值的位置，这些就是文本的语义转折点，用于分割不同的主题块。

7. 可视化展示
   生成图表显示：

   • 蓝色曲线：28个位置的语义距离变化
   • 红色水平线：95%分位数阈值
   • 彩色区域：不同的语义块
   • 红色圆点：标记的断点位置

开始计算语义距离...
分割出 29 个句子:
1. One of the most important things I didn't understand about the world when I was a child is the degre...
2. Teachers and coaches implicitly told us the returns were linear....
3. "You get out," I heard a thousand times, "what you put in." They meant well, but this is rarely true...
4. If your product is only half as good as your competitor's, you don't get half as many customers....
5. You get no customers, and you go out of business....
6. It's obviously true that the returns for performance are superlinear in business....
7. Some think this is a flaw of capitalism, and that if we changed the rules it would stop being true....
8. But superlinear returns for performance are a feature of the world, not an artifact of rules we've i...
9. We see the same pattern in fame, power, military victories, knowledge, and even benefit to humanity....
10. In all of these, the rich get richer....
11. [1]

You can't understand the world without understanding the concept of superlinear returns....
12. And if you're ambitious you definitely should, because this will be the wave you surf on....
13. It may seem as if there are a lot of different situations with superlinear returns, but as far as I ...
14. The most obvious case of superlinear returns is when you're working on something that grows exponent...
15. For example, growing bacterial cultures....
16. When they grow at all, they grow exponentially....
17. But they're tricky to grow....
18. Which means the difference in outcome between someone who's adept at it and someone who's not is ver...
19. Startups can also grow exponentially, and we see the same pattern there....
20. Some manage to achieve high growth rates....
21. Most don't....
22. And as a result you get qualitatively different outcomes: the companies with high growth rates tend ...
23. Y Combinator encourages founders to focus on growth rate rather than absolute numbers....
24. It prevents them from being discouraged early on, when the absolute numbers are still low....
25. It also helps them decide what to focus on: you can use growth rate as a compass to tell you how to ...
26. But the main advantage is that by focusing on growth rate you tend to get something that grows expon...
27. YC doesn't explicitly tell founders that with growth rate "you get out what you put in," but it's no...
28. And if growth rate were proportional to performance, then the reward for performance p over time t w...
29. Even after decades of thinking about this, I find that sentence startling....

生成嵌入向量...
计算出 28 个距离值
距离值: ['0.020', '0.048', '0.048', '0.058', '0.047', '0.036', '0.036', '0.033', '0.030', '0.068', '0.059', '0.020', '0.042', '0.022', '0.083', '0.059', '0.063', '0.019', '0.035', '0.096', '0.067', '0.011', '0.028', '0.064', '0.042', '0.045', '0.014', '0.048']

95%分位数阈值: 0.077
超过阈值的距离数量: 2
最终块数: 3
断点位置: [14, 19]

==================================================
使用SemanticChunker验证结果:
SemanticChunker分割结果: 3 个块

块 1 (1414 字符):
One of the most important things I didn't understand about the world when I was a child is the degree to which the returns for performance are superlinear. Teachers and coaches implicitly told us the ...

块 2 (299 字符):
When they grow at all, they grow exponentially. But they're tricky to grow. Which means the difference in outcome between someone who's adept at it and someone who's not is very great. Startups can al...

块 3 (935 字符):
Most don't. And as a result you get qualitatively different outcomes: the companies with high growth rates tend to become immensely valuable, while the ones with lower growth rates may not even surviv...

总字符数: 2658
平均块大小: 886.0 字符

基于模型的端到端语义分块

更先进的方法是使用专门训练的神经网络模型，直接判断每个句子是否应作为分块点。这种方法无需手动设置阈值，而是由模型端到端地完成分块决策。

以阿里达摩院开发的语义分块模型为例，其工作流程为：

1. 将文本窗口中的N个句子输入模型
2. 模型为每个句子生成表示向量
3. 通过二分类层直接判断每个句子是否为分块点
   

from modelscope.pipelines import pipeline

# 加载语义分块模型
semantic_segmentation = pipeline(
    'text-semantic-segmentation',
    model='damo/nlp_bert_semantic-segmentation_chinese-base'
)

# 进行分块
result = semantic_segmentation(long_text)
segments = result['text']

这种方法的优势在于模型已经学习了语义变化的复杂模式，无需手动调整参数。但需注意模型的泛化能力，应在特定领域文档上进行验证。

5. 父文档检索（分层切割）

父文档检索器的核心思想其实很简单：用小块来检索，用大块来回答。这样做的好处显而易见：我们获得了子块级别的检索精度，同时保持了父块级别的上下文丰富度。

具体的工作流程是这样的：

1. 分层分块：首先将原始文档分成较大的父块，然后将每个父块进一步分割成更小的子块。若是不分块即为全文，若是分块即分层。
2. 索引子块：对这些小的子块进行向量化并建立索引
3. 检索时的魔法：当用户提问时，系统会基于子块的嵌入进行相似度搜索，但返回的不是子块本身，而是包含该子块的父块

下图展示了分层的父文档构建过程：

举个例子，假设用户问"腾讯的广告收入是多少"，系统可能会匹配到一个专门讨论广告收入数字的小块，但返回的是包含完整财务分析上下文的大块，这样LLM就能基于更全面的信息来回答问题。涉及到向量检索，我们通常是采用向量数据库存储从而实现检索（后续代码可以体现）。

dify中2025年集成了父子检索，且将其作为推荐分块，如下图：

父文档检索器有两种常见的实现方式：

方式一：返回完整文档

如果你的原始文档本身就不是特别长（比如产品说明书、新闻文章等），可以直接将完整文档作为"父块"。这种情况下：

• 子块：文档的段落或句子
• 父块：完整的文档

这种方式特别适合处理大量相对短小的文档集合，比如FAQ数据库、产品目录等。

from langchain_community.embeddings import HuggingFaceBgeEmbeddings
from langchain.retrievers import ParentDocumentRetriever
from langchain.storage import InMemoryStore
from langchain.vectorstores import Chroma
from langchain_text_splitters import RecursiveCharacterTextSplitter
from langchain_core.documents import Document
import os

os.environ['HF_ENDPOINT'] = 'https://hf-mirror.com'

model_name = "BAAI/bge-small-en"
model_kwargs = {"device": "cpu"}
encode_kwargs = {"normalize_embeddings": True}
bge_embeddings = HuggingFaceBgeEmbeddings(
    model_name=model_name, model_kwargs=model_kwargs, encode_kwargs=encode_kwargs
)

document="""One of the most important things I didn't understand about the world when I was a child is the degree to which the returns for performance are superlinear.

Teachers and coaches implicitly told us the returns were linear. "You get out," I heard a thousand times, "what you put in." They meant well, but this is rarely true. If your product is only half as good as your competitor's, you don't get half as many customers. You get no customers, and you go out of business.

It's obviously true that the returns for performance are superlinear in business. Some think this is a flaw of capitalism, and that if we changed the rules it would stop being true. But superlinear returns for performance are a feature of the world, not an artifact of rules we've invented. We see the same pattern in fame, power, military victories, knowledge, and even benefit to humanity. In all of these, the rich get richer. [1]

You can't understand the world without understanding the concept of superlinear returns. And if you're ambitious you definitely should, because this will be the wave you surf on.

It may seem as if there are a lot of different situations with superlinear returns, but as far as I can tell they reduce to two fundamental causes: exponential growth and thresholds.

The most obvious case of superlinear returns is when you're working on something that grows exponentially. For example, growing bacterial cultures. When they grow at all, they grow exponentially. But they're tricky to grow. Which means the difference in outcome between someone who's adept at it and someone who's not is very great.

Startups can also grow exponentially, and we see the same pattern there. Some manage to achieve high growth rates. Most don't. And as a result you get qualitatively different outcomes: the companies with high growth rates tend to become immensely valuable, while the ones with lower growth rates may not even survive.

Y Combinator encourages founders to focus on growth rate rather than absolute numbers. It prevents them from being discouraged early on, when the absolute numbers are still low. It also helps them decide what to focus on: you can use growth rate as a compass to tell you how to evolve the company. But the main advantage is that by focusing on growth rate you tend to get something that grows exponentially.

YC doesn't explicitly tell founders that with growth rate "you get out what you put in," but it's not far from the truth. And if growth rate were proportional to performance, then the reward for performance p over time t would be proportional to pt.

Even after decades of thinking about this, I find that sentence startling."""


child_splitter = RecursiveCharacterTextSplitter(chunk_size=100, chunk_overlap=0)
docs = child_splitter.create_documents([document])

vectorstore = Chroma(
    collection_name="documents", embedding_function=bge_embeddings
)


store = InMemoryStore()
retriever = ParentDocumentRetriever(
    vectorstore=vectorstore,
    docstore=store,
    child_splitter=child_splitter
)

retriever.add_documents([Document(page_content=document)], ids=None)

# 返回小文档检索，问题：什么原因造成了超线性回报？
sub_docs = vectorstore.similarity_search("What causes superlinear returns?")

# 返回大文档检索
retrieved_docs = retriever.get_relevant_documents("What causes superlinear returns?")
print(sub_docs[0].page_content)
print('='*40)
print(retrieved_docs[0].page_content)

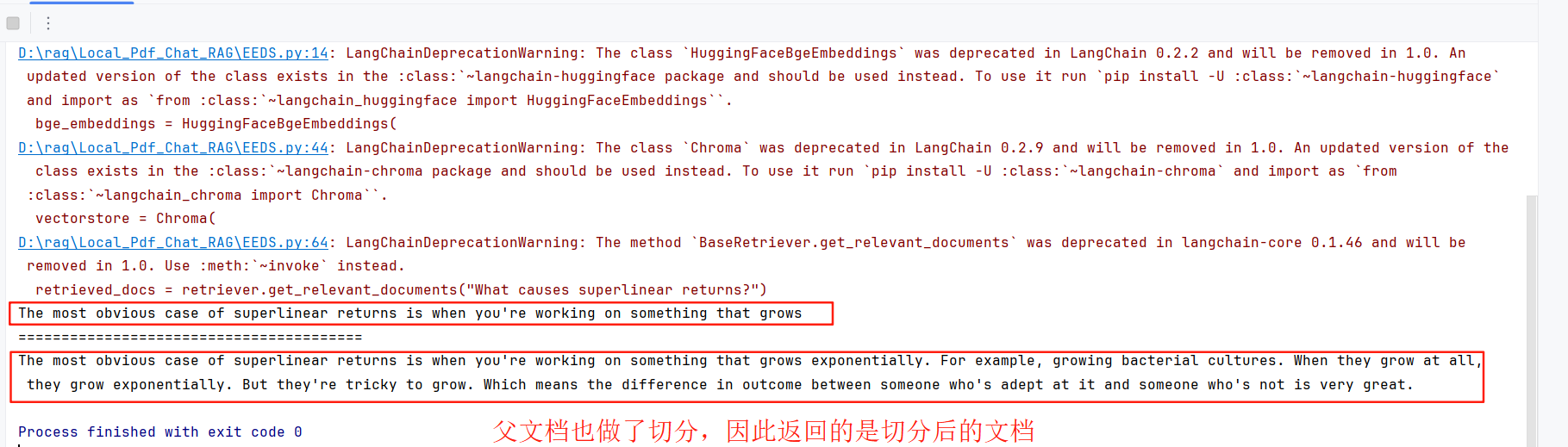
控制台的输出：

方式二：分层块结构

对于长文档，我们需要建立真正的分层结构：

• 原始文档 → 父块（比如400字符）→ 子块（比如100字符）

这种方式更适合处理长报告、学术论文、技术文档等。
这部分代码与方式一很类似：

from langchain_community.embeddings import HuggingFaceBgeEmbeddings
from langchain.retrievers import ParentDocumentRetriever
from langchain.storage import InMemoryStore
from langchain.vectorstores import Chroma
from langchain_text_splitters import RecursiveCharacterTextSplitter
from langchain_core.documents import Document
import os

os.environ['HF_ENDPOINT'] = 'https://hf-mirror.com'

model_name = "BAAI/bge-small-en"
model_kwargs = {"device": "cpu"}
encode_kwargs = {"normalize_embeddings": True}
bge_embeddings = HuggingFaceBgeEmbeddings(
    model_name=model_name, model_kwargs=model_kwargs, encode_kwargs=encode_kwargs
)

document="""One of the most important things I didn't understand about the world when I was a child is the degree to which the returns for performance are superlinear.

Teachers and coaches implicitly told us the returns were linear. "You get out," I heard a thousand times, "what you put in." They meant well, but this is rarely true. If your product is only half as good as your competitor's, you don't get half as many customers. You get no customers, and you go out of business.

It's obviously true that the returns for performance are superlinear in business. Some think this is a flaw of capitalism, and that if we changed the rules it would stop being true. But superlinear returns for performance are a feature of the world, not an artifact of rules we've invented. We see the same pattern in fame, power, military victories, knowledge, and even benefit to humanity. In all of these, the rich get richer. [1]

You can't understand the world without understanding the concept of superlinear returns. And if you're ambitious you definitely should, because this will be the wave you surf on.

It may seem as if there are a lot of different situations with superlinear returns, but as far as I can tell they reduce to two fundamental causes: exponential growth and thresholds.

The most obvious case of superlinear returns is when you're working on something that grows exponentially. For example, growing bacterial cultures. When they grow at all, they grow exponentially. But they're tricky to grow. Which means the difference in outcome between someone who's adept at it and someone who's not is very great.

Startups can also grow exponentially, and we see the same pattern there. Some manage to achieve high growth rates. Most don't. And as a result you get qualitatively different outcomes: the companies with high growth rates tend to become immensely valuable, while the ones with lower growth rates may not even survive.

Y Combinator encourages founders to focus on growth rate rather than absolute numbers. It prevents them from being discouraged early on, when the absolute numbers are still low. It also helps them decide what to focus on: you can use growth rate as a compass to tell you how to evolve the company. But the main advantage is that by focusing on growth rate you tend to get something that grows exponentially.

YC doesn't explicitly tell founders that with growth rate "you get out what you put in," but it's not far from the truth. And if growth rate were proportional to performance, then the reward for performance p over time t would be proportional to pt.

Even after decades of thinking about this, I find that sentence startling."""


child_splitter = RecursiveCharacterTextSplitter(chunk_size=100, chunk_overlap=0)
docs = child_splitter.create_documents([document])

# add：增加了parent_splitter这句
parent_splitter = RecursiveCharacterTextSplitter(chunk_size=400)
vectorstore = Chroma(
    collection_name="documents", embedding_function=bge_embeddings
)


store = InMemoryStore()
retriever = ParentDocumentRetriever(
    vectorstore=vectorstore,
    docstore=store,
    child_splitter=child_splitter,
    # add
    parent_splitter=parent_splitter
)

retriever.add_documents([Document(page_content=document)], ids=None)

# 返回小文档检索，问题：什么原因造成了超线性回报？
sub_docs = vectorstore.similarity_search("What causes superlinear returns?")

# 返回大文档检索
retrieved_docs = retriever.get_relevant_documents("What causes superlinear returns?")
print(sub_docs[0].page_content)
print('='*40)
print(retrieved_docs[0].page_content)