NLP学习路线图（十六）：N-gram模型

一、为何需要语言模型？概率视角下的语言本质

自然语言处理的核心挑战在于让机器“理解”人类语言。这种理解的一个关键方面是处理语言的歧义性、创造性和结构性。语言模型（Language Model, LM）为此提供了一种强大的数学框架：它赋予任何词序列一个概率，用以衡量该序列在真实语言中出现的可能性。

1.1 语言模型的核心任务

评估序列合理性：判断一个句子“The cat sat on the mat”是否比“Mat the on sat cat the”更像人话。
预测下一个词：给定上文“I have a dream...”，预测下一个最可能出现的词（如“that”）。
生成连贯文本：基于概率采样，逐步生成新的、语法语义合理的句子。

1.2 统计语言模型的兴起

在早期NLP中，基于规则的方法试图用语法书般的精确规则描述语言，但很快遇到瓶颈：人类语言充满例外、方言和动态变化，规则难以穷尽。统计语言模型应运而生，其核心理念是：

“一个词出现的可能性，可以由它在大量文本数据中出现的频率来估计。”

N-gram模型正是这一理念最直接、最成功的实现之一。

二、N-gram模型：概念与数学基础

2.1 核心定义

N-gram：指文本中连续出现的N个词（或符号）单元。例如：
- Unigram (1-gram): ["the"], ["cat"], ["sat"]
- Bigram (2-gram): ["the", "cat"], ["cat", "sat"]
- Trigram (3-gram): ["the", "cat", "sat"]
N-gram语言模型：一个基于马尔可夫假设的统计模型，它假设一个词出现的概率仅依赖于它前面的有限个词（通常是N-1个）。这是对现实语言复杂依赖关系的一种简化，但实践证明非常有效。

2.2 数学建模：链式法则与马尔可夫假设

语言模型的目标是为整个词序列W = (w1, w2, ..., wm) 赋予概率P(W)。根据概率的链式法则：
P(W) = P(w1) * P(w2|w1) * P(w3|w1, w2) * ... * P(wm|w1, w2, ..., wm-1)

精确计算P(wm|w1, w2, ..., wm-1)需要知道所有可能的历史组合的概率，这在数据有限时几乎不可能。马尔可夫假设提供了简化方案：假设一个词的概率只依赖于前面有限的k个词。当k = N-1时，我们得到N-gram模型：

P(wm|w1, w2, ..., wm-1) ≈ P(wm|wm-N+1, wm-N+2, ..., wm-1)

因此，序列概率近似为：
P(W) ≈ Π P(wi|wi-N+1, ..., wi-1)

2.3 概率估计：最大似然估计（MLE）

模型参数P(wi|wi-N+1, ..., wi-1)如何获得？最直观的方法是在大型训练语料库中计数：

P(wi | wi-N+1, ..., wi-1) = Count(wi-N+1, ..., wi-1, wi) / Count(wi-N+1, ..., wi-1)

Count(wi-N+1, ..., wi-1, wi)：特定N-gram序列在语料中出现的次数。
Count(wi-N+1, ..., wi-1)：该序列的历史上下文（前N-1个词）出现的次数。

示例： 在语料“the cat sat on the mat”中：

P(sat | the cat) = Count(the cat sat) / Count(the cat) = 1 / 1 = 1.0
P(mat | on the) = Count(on the mat) / Count(on the) = 1 / 1 = 1.0

三、构建N-gram模型：从数据到应用

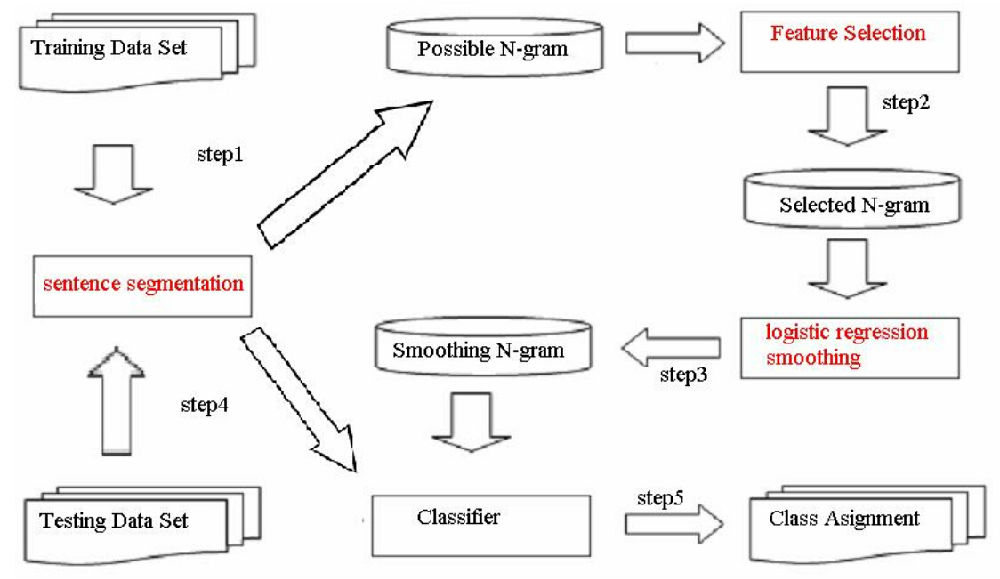
3.1 训练流程

数据收集与预处理：收集大规模、领域相关的文本数据。进行分词、去除标点/数字（可选）、统一大小写、处理OOV词（如替换为<UNK>）。
计数统计：扫描语料，统计所有1-gram, 2-gram, ..., N-gram的出现频次。通常使用高效的数据结构（如哈希表、前缀树）。
概率计算：应用MLE公式计算所有条件概率P(wi | context)。
平滑处理（关键！）：处理零概率问题（见下一节）。
模型存储：存储计算好的概率表（通常很大，需优化）。

3.2 解码与应用：预测与生成

下一个词预测：给定上下文(wi-N+1, ..., wi-1)，查找概率P(w | wi-N+1, ..., wi-1)最大的词w。
序列概率评估：利用链式法则计算整个序列的概率（通常取对数避免下溢）。
文本生成：
1. 给定起始词（或<S>标记）。
2. 基于当前上下文（最后N-1个词），根据概率分布P(w | context)采样下一个词。
3. 将采样词加入序列，更新上下文。
4. 重复步骤2-3，直到生成结束标记</S>或达到长度限制。

四、挑战与对策：平滑技术详解

MLE估计的最大问题是数据稀疏性：语料库再大，也无法覆盖所有可能的N-gram组合。未在训练集中出现的N-gram（零频问题）会直接导致概率为零，进而使整个序列的概率为零，这显然不合理。平滑（Smoothing） 技术通过“劫富济贫”来解决此问题。

4.1 核心思想

为所有可能的N-gram（即使未出现）分配非零概率。
从高频N-gram的概率中“借”一小部分，分配给低频或零频N-gram。
确保所有概率之和为1。

4.2 常用平滑方法

加一平滑（拉普拉斯平滑）：
- 最简单直观。
- 公式：P(wi | wi-N+1, ..., wi-1) = (Count(wi-N+1, ..., wi-1, wi) + 1) / (Count(wi-N+1, ..., wi-1) + V)
- V：词汇表大小。
- 优点：实现简单。
- 缺点：对高频N-gram概率削减过多；对于大N或大V，分配的概率太小，效果常不理想。
加K平滑（Lidstone平滑）：
- 加一平滑的推广，加一个小的常数k(0 < k < 1)。
- 公式：P = (Count + k) / (Count_Context + k * V)
- 通过调整k可以在偏差和方差间取得平衡。
古德-图灵估计（Good-Turing）：
- 更智能的平滑。核心思想：用观察到的出现r次的N-gram数量，来估计出现r次的事物的总概率质量，并将其分配给未出现（r=0）的事物。
- 计算调整频次：r* = (r+1) * N(r+1) / N(r)，其中N(r)是出现r次的N-gram类型数。
- 将频次为0的N-gram概率估计为：P = N(1) / N（N是总token数）。
- 优点：理论基础坚实，效果较好。
- 缺点：计算复杂，需统计所有频次N(r)；对于高频r，N(r)可能为0或不稳定。
回退（Backoff）：
- 核心思想：如果一个高阶N-gram（如trigram）没有数据，就“回退”到低阶N-gram（如bigram或unigram）的估计。
- 条件：通常仅在Count(HighOrderNgram) = 0时触发回退。
- 概率分配：高阶概率为0时，使用低阶概率乘以一个回退权重α（α < 1），以确保总概率质量守恒。
- 公式（以trigram回退到bigram为例）：
```
P(wi | wi-2, wi-1) = {
    Count(wi-2, wi-1, wi) / Count(wi-2, wi-1)   if Count(wi-2, wi-1, wi) > 0
    α(wi-2, wi-1) * P(wi | wi-1)               otherwise
}
```
- 权重计算：α需要精心设计，保证在wi-2, wi-1条件下，所有词的概率和为1。
插值（Interpolation）：
- 核心思想：无论高阶N-gram是否存在数据，总是将不同阶（unigram, bigram, trigram, ...）的估计混合起来。
- 公式（以trigram插值为例）：
  P(wi | wi-2, wi-1) = λ1 * P(wi) + λ2 * P(wi | wi-1) + λ3 * P(wi | wi-2, wi-1)
- 约束：λ1 + λ2 + λ3 = 1，λi >= 0。
- 优点：更鲁棒，即使高阶gram有数据，低阶gram也能提供有价值信息，防止过拟合。
- 权重学习：λ参数通常通过在留存数据集（held-out data）上优化模型困惑度（Perplexity）来学习。
Kneser-Ney平滑：
- 被广泛认为是效果最佳的N-gram平滑方法之一，结合了回退和绝对折扣的思想。
- 核心创新（主要在unigram概率上）：
  - 延续概率（Continuation Probability）：低阶模型（如unigram）不再仅基于词频，而是考虑一个词出现在不同上下文类型中的多样性。
  - 公式（以bigram Kneser-Ney为例）：
```
P_KN(wi | wi-1) = max(Count(wi-1, wi) - D, 0) / Count(wi-1)  + λ(wi-1) * P_Continuation(wi)
P_Continuation(wi) = |{v: Count(v, wi) > 0}| / |{(u, v): Count(u, v) > 0}|
```
  - D：折扣常数（通常0.75左右）。
  - λ(wi-1)：归一化因子，保证概率和为1。
  - P_Continuation(wi)：衡量wi作为新上下文“接续词”的能力。想象“Francisco”在“San Francisco”中频率高，但单独作为接续词能力弱（主要接在“San”后）；而“cup”则可能出现在“coffee cup”, “world cup”等多种上下文中，其P_Continuation较高。
- 优点：显著提高了对低频词和未知上下文的建模能力。
- 变种：Modified Kneser-Ney (MKN) 使用多个折扣值（对不同频次）。

下表总结了主要平滑方法的比较：

平滑方法	核心思想	优点	缺点	适用场景
加一(拉普拉斯)	所有计数+1	实现极其简单	高频项概率削减过多，效果常不佳	教学示例，快速原型
加K平滑	所有计数 + k (0<k<1)	比加一灵活，可调参数	k值选择需经验或优化，高频项仍被削	对简单加一的改进
古德-图灵	用出现r次类型数估计r*概率	理论基础好，对零频项估计合理	计算复杂，高频估计不稳定	需要较好理论基础的中小模型
回退	高阶无数据时回退到低阶	直觉清晰，实现相对直接	权重设计复杂，仅高阶缺失时才用低阶	资源受限，需显式回退逻辑
插值	混合不同阶模型，加权平均	更鲁棒，充分利用各级信息	需学习权重参数，计算开销稍大	追求最佳效果的通用场景
Kneser-Ney	折扣+回退+独特接续概率	公认效果最好	实现最复杂，计算开销最大	对性能要求高的生产系统

五、N-gram模型的应用场景

尽管相对“传统”，N-gram模型凭借其高效、简单和可解释性，在众多场景中仍有一席之地，或作为更复杂系统的组件：

文本输入法：
- 核心应用！基于用户输入的前几个词（或拼音音节），预测下一个最可能的候选词。
- Bigram/Trigram模型在此任务上非常高效且有效。
- 例如：输入“wo xiang”，模型基于“我想”的历史，高概率预测“吃”、“要”、“买”等词。
拼写检查与语法纠错：
- 检测低概率词序列。句子“I are a student”中“I are”的bigram概率会极低，触发错误警报。
- 结合词典和混淆集，用于建议纠正（如“are”-> “am”）。
语音识别：
- 声学模型识别出多个可能的词序列候选。
- 语言模型（通常是trigram或更高阶）用于评估哪个词序列在语言上更“合理”，对识别结果进行重排序。如“recognize speech” vs. “wreck a nice beach”。
机器翻译（早期统计机器翻译SMT）：
- SMT的核心组件之一（与翻译模型配合）。用于评估翻译输出的目标语言流畅度。
- 生成的目标语言句子概率越高，通常意味着越流畅自然。
信息检索：
- 查询扩展：利用同文档/相关文档中的高频共现词（N-gram）扩展用户原始查询。
- 文档排序：部分早期模型（如查询似然模型）将文档视为语言模型生成查询的概率源，N-gram是其基础。
- 相关性反馈：根据相关文档中的显著N-gram调整查询。
文本分类与情感分析：
- 将N-gram（特别是unigram和bigram）作为强大的文本特征。
- 分类器（如Naive Bayes, SVM）学习不同类别（如体育/财经/娱乐；正面/负面）下N-gram特征的分布差异。
- 例如：“暴跌”、“涨停”、“市盈率”等bigram在财经类中概率高；“进球”、“射门”、“点球”在体育类中概率高。
生物信息学（DNA/蛋白质序列分析）：
- 将生物序列（A/T/C/G 或氨基酸）视为“文本”。
- N-gram模型用于识别保守序列模式、基因预测、序列比对等。

六、N-gram的局限性与现代NLP中的演变

6.1 固有局限性

数据稀疏性：核心挑战，催生了平滑技术，但问题无法根除。长尾N-gram难以准确建模。
上下文窗口有限（马尔可夫假设）：只能捕捉局部依赖（N-1词），无法建模长距离依赖（如主谓一致跨越从句）。例如：“The keys to the cabinet are on the table” vs. “The key to the cabinets is...”。
缺乏语义理解：基于共现统计，无法真正理解词义、语义角色、逻辑关系。无法处理同义（“buy/purchase”）、反义（“hot/cold”）或隐喻。
维度灾难：N增大时，可能的N-gram组合数量呈指数级增长（O(V^N)），导致存储和统计需求爆炸。实践中N很少超过5。
领域依赖性：在特定领域语料上训练的N-gram模型，移植到其他领域效果会显著下降（词汇、表达方式不同）。

6.2 现代NLP中的传承与演变

尽管有局限，N-gram的思想并未消亡，而是以不同形式融入现代NLP：

神经语言模型的基础：
- Bengio在2003年提出的前馈神经网络语言模型是神经语言模型的先驱。它使用词嵌入表示词，并通过神经网络学习P(wi | wi-1, ..., wi-n+1)。它突破了离散表示和手工特征的局限，但仍基于固定窗口（N-gram）上下文。这直接启发了后来的RNN/LSTM/Transformer。
子词单元（Subword Units）：
- 现代模型（如BERT, GPT）普遍采用Byte Pair Encoding (BPE), WordPiece, Unigram LM等算法将词分割为更小的子词单元（如"un", "##able", "ization"）。
- 这些子词单元本身可以看作是一种动态的、数据驱动的“N-gram”或字符组合，有效缓解了OOV问题和数据稀疏性，同时允许模型学习词素级别的规律。
Transformer中的局部注意力（有时）：
- 虽然Transformer的自注意力机制原则上可以捕获任意长距离依赖，但为了提高效率或引入归纳偏置，有时会使用受限（窗口）注意力。例如：
  - 局部窗口注意力：只关注当前位置前后固定窗口内的词（如邻居100个词），这本质上是在学习一种软化的、基于上下文的N-gram模型。
  - 稀疏注意力模式（如Longformer, BigBird）：包含局部窗口注意力作为其模式的一部分。
- 这些设计表明，局部依赖关系（N-gram的核心）在语言中仍然至关重要，并且高效捕获它们仍然有价值。
特征工程的基石：
- 在深度学习模型中，N-gram特征（尤其是unigram, bigram）仍然常被作为输入特征或与神经网络的输出拼接，为模型提供显式的、强局部信号。例如，在文本分类或简单序列标注任务中，N-gram特征结合神经网络能取得很好效果。
轻量级解决方案与基线：
- 在资源受限（如嵌入式设备、低延迟场景）或数据量不大的任务中，平滑良好的N-gram模型因其极高的效率、低计算开销和易于部署的特点，仍然是可行的选择。
- 它也是评估更复杂模型进步的重要基线。如果一个强大的神经模型在某个任务上无法显著超越精心调优的N-gram模型，可能意味着任务本身特性或模型设计存在问题。