一、决策树

1. 决策树有一个很强的假设：

    信息是可分的，否则无法进行特征分支

2. 决策树的种类：

2. ID3决策树：

ID3决策树的数划分标准是信息增益：

信息增益衡量的是通过某个特征进行数据划分前后熵的变化量。但是，它没有考虑到特征本身的熵，因此容易偏向于取值较多的特征。

3. C4.5决策树：

C4.5决策树的数划分标准是信息增益比：

信息增益比则是 信息增益 除以 该特征自身的熵（也称为分裂信息）。这种方法旨在纠正信息增益对于取值较多特征的偏爱，通过将信息增益与特征自身的熵相除来惩罚那些拥有大量取值的特征。

C4.5并没有直接偏向于取值少的特征，而是通过分裂信息来调整信息增益，使得特征的基数大小影响其最终的选择概率。这种方式帮助算法避免了仅仅基于信息增益选择特征可能导致的过拟合问题，特别是当存在高基数特征时。

4. CART 回归树 和 分类树：

回归树：每个子树的输出是该子树节点值的均值：

步骤(1)：选择最优切分变量和切分点

步骤(2)：划分区域并决定输出值 

根据特征jj和切分点ss将数据集划分为两个子区域

计算子区域内的样本目标值的平均值作为该区域的预测值

这两个步骤描述了递归地应用上述过程，直到满足停止条件，并最终生成决策树的过程。

5. CART 的参数： 

6. CART 训练后的回归树常用属性：

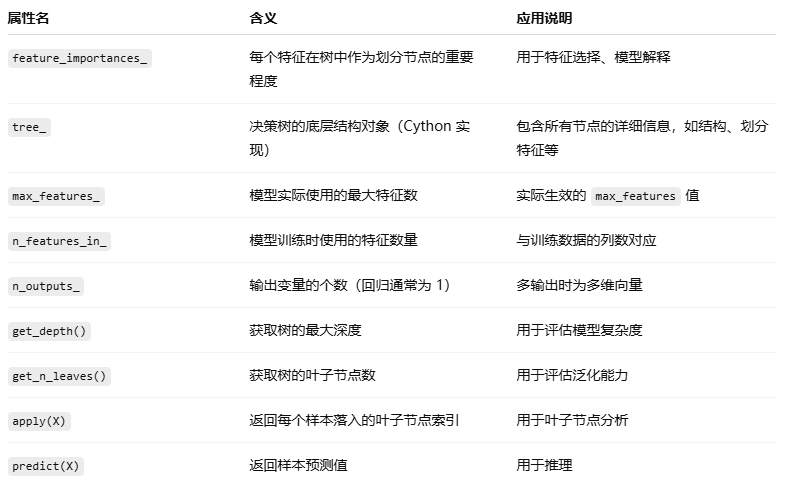
为什么获取树的叶子节点数 就可以用于评估泛化能力？

       叶子节点数量越多，意味着决策树越复杂。每个叶子节点代表一个具体的预测规则或输出值。如果一棵树的叶子节点过多，说明它可能已经学习了训练数据中的很多细节甚至是噪音，这种现象通常被称为过拟合。过拟合模型在训练集上表现很好，但在未见过的数据（测试集）上的表现较差。

7. 回归树demo展示，可视化回归树：

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeRegressor, plot_tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt

# 1. 加载数据
data = load_iris()
X = data.data
y = X[:, 0]  # 用 sepal length 做回归目标

# 2. 数据划分
X_train, X_test, y_train, y_test = train_test_split(X[:, 1:], y, test_size=0.2, random_state=42)

# 3. 建立模型
reg = DecisionTreeRegressor(max_depth=3, random_state=42)
reg.fit(X_train, y_train)

# 4. 模型预测与评估
y_pred = reg.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f"\n【模型评估】\n均方误差 MSE: {mse:.4f}")

# 5. 打印常用属性
print("\n【模型属性展示】")
print("特征重要性 feature_importances_:", reg.feature_importances_)
print("使用特征数 n_features_in_:", reg.n_features_in_)
print("输出维度数 n_outputs_:", reg.n_outputs_)
print("实际使用的 max_features_:", reg.max_features_)
print("树最大深度 get_depth():", reg.get_depth())
print("叶子节点数 get_n_leaves():", reg.get_n_leaves())

# 6. 可视化特征重要性
feature_names = data.feature_names[1:]
plt.figure(figsize=(6, 4))
plt.bar(feature_names, reg.feature_importances_, color='teal')
plt.title("Feature Importances")
plt.ylabel("Importance")
plt.grid(axis='y')
plt.tight_layout()
plt.show()

# 7. 可视化树结构
plt.figure(figsize=(10, 6))
plot_tree(reg, feature_names=feature_names, filled=True, rounded=True)
plt.title("Decision Tree Structure")
plt.show()

8. 分类树：

sklearn 的模型参数：

模型属性对比：

demo：

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 1. 数据准备
iris = load_iris()
X = iris.data
y = iris.target

# 2. 划分数据
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 3. 构建模型（使用信息增益）
clf = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=42)
clf.fit(X_train, y_train)

# 4. 预测与评估
y_pred = clf.predict(X_test)
acc = accuracy_score(y_test, y_pred)
print(f"准确率: {acc:.4f}")

# 5. 展示分类专有属性
print("\n【分类树专有属性】")
print("类别标签 classes_:", clf.classes_)
print("类别数量 n_classes_:", clf.n_classes_)
print("每个测试样本的预测概率 predict_proba():\n", clf.predict_proba(X_test[:5]))

 二、Boosting：

（1）Boosting 中文是“提升方法”，是一种集成学习方法，它只是一个“策略思想”。

（2）AdaBoost、GDBT、 XGBoost、LightGBM 都是这个思想的具体实现。

（3）Boosting 将多个弱学习器（weak learner），如小决策树，串行地组合在一起，每一轮都“纠正”上一轮的错误，最终得到一个强大的集成模型。

（4）Gradient Boosting：英文缩写 GDBT ，中文是“梯度提升树”或“提升树”、“提升树模型”。

（5）注意：提升树 ≈ GBDT（及其变种） ≠  AdaBoost 

1. AdaBoost：

注意：不同于GDBT，AdaBoost 在第 t 轮不直接使用前一轮训练出的模型，而是通过样本权重的改变，间接地反映之前模型的表现。

AdaBoost 每一轮都是从头训练一个新的弱学习器   ，只是通过每次迭代将 训练样本分布进行调整，令错分样本权重更大

2. GDBT：

GBDT 是一种通过迭代拟合损失函数负梯度（即残差）的方式训练多个决策树并进行加权求和的Boosting 方法。GDBT使用回归树作为弱学习器（哪怕是分类任务）。

GBDT 的“Gradient”不是装饰，它真的是在做梯度下降，只是回归时，常用的损失函数是平方误差（MSE）的公式为：

 

对于MSE 的负梯度为：

MSE的负梯度刚好有一个可描述的名字，就是残差，因此可以理解为一种巧合hh

再举个例子：

GBDT 用于二分类，使用对数损失（Log Loss）：

那么，在 GBDT 的每一轮中，就是用这些 负梯度 gi​ 作为新的“伪标签”来训练一个 回归树。在新的一轮迭代中，这个回归树试图学习xi → gi 。该回归树不是去做分类，而是用回归树去逼近这个负梯度值（伪残差）

你看到的是“残差”，其实它背后是“负梯度”；
这个巧合让 GBDT 在回归问题上看起来像“残差堆树”，但本质上是一种通用的函数空间梯度优化方法。

三、GDBT算法：

1. 算法步骤：

解释一下 GDBT的初始化：如果设定 ，那第一步的残差就是 ，计算更简单

2. GDBT 模型过拟合分析：

GDBT 算法通过逐次拟合残差并不断优化模型，能够有效地提高模型的预测精度，且避免模型过拟合，具体来说，原因如下：

（1）逐步拟合残差，避免直接过拟合目标
每一步学习的目标是上一步的误差（残差），不是一次性“猜中全部”。这种“加法模型”方式可以让模型以小步慢走的方式逐渐逼近真实目标。

（2）模型弱但组合强
Boosting 通常使用弱学习器（如深度很浅的决策树）。单个模型能力弱，不容易过拟合，但组合起来又能表现强。

3. GDBT 如何解决分类问题：

GBDT 是一个加法模型，不断拟合前一轮的负梯度（即残差）来逼近真实目标。

对于分类问题，GBDT 并不是直接输出类别，而是构造一个连续值 f(x) ，被称作 logit 值，然后通过某种映射函数（比如 sigmoid 或 softmax）得到概率 P(x)，用概率和真实标签计算 loss，更新树。树学习完毕，通过映射函数（比如 sigmoid 或 softmax）得到概率 P(x)再进行分类。

GBDT 的本质是：

• 模型输出 logit 值 f(x)f(x)f(x)；

• 然后通过 sigmoid 转为概率 p(x)p(x)p(x)；

• 然后用概率和真实标签计算 loss，更新树。

3.1 二分类问题：

二分类问题的损失函数 和 根据推理出的连续预测值判断类别的方式如下：

3.2 多分类问题：

4. GDBT + LR模型组合方案 实现 特征交叉组合

总结起来：在大规模 CTR 预估中，利用 GBDT 自动学习复杂的特征交叉组合，用 GBDT 自动做特征组合/交叉，然后将其结果转换为稀疏的 one-hot 向量，作为 LR 的输入特征。

可以说：在这个组合中，将GDBT作为encoder， LR作为decoder

4.1 解释一下LR的缺点：

在传统的逻辑回归（Logistic Regression）中，模型对特征之间的关系是线性加和的。假设你有两个离散特征：gender = female（性别为女性），device = mobile（使用移动设备）

你希望模型能够捕捉到这样一个复杂的行为模式：“女性使用移动设备时，点击率特别高；但在其他设备上，或者男性用户，点击率就不高。”

这就是一个特征组合效应。然而，逻辑回归本身并不能自动建模这种“组合条件”。它只会分别给gender=female 一个权重；device=mobile 一个权重；

但无法表达 gender=female ∧ device=mobile 这个组合的交互含义。模型会把两个特征的权重加起来，却看不到它们组合在一起时可能呈现出的非线性行为。

为了解决这个问题，通常需要手工构造一个交叉特征 ：cross_feature = (gender == female) AND (device == mobile)  这个新特征就相当于告诉模型：“这是一个特殊情况，需要关注”。然后把它作为新的输入特征加入逻辑回归模型中

因此，我们常说：

逻辑回归无法自动发现复杂的特征组合和非线性关系，必须依赖人工交叉特征，成本高、依赖专家经验和领域知识。

这正是 GBDT 等非线性模型能发挥优势的地方 —— 它们可以自动建模复杂交互关系，无需大量人工特征工程。

同时，逻辑回归属于线性模型，它的决策边界是线性的。如果点击行为的边界是非线性的，比如弯曲的、环形的，逻辑回归就无法很好拟合，因为它只能切直线。GBDT 通过决策树的分裂，自动学习特征之间的组合和非线性；神经网络通过非线性激活函数和多层结构，也能自动学复杂关系；这样将两者互补就可以很好的解决工业上面对的问题。

4.2 具体实现流程：

 

 

5. GDBT 的优缺点：

6. GDBT 与 随机森林 的区别：

四、XGBoost 算法：

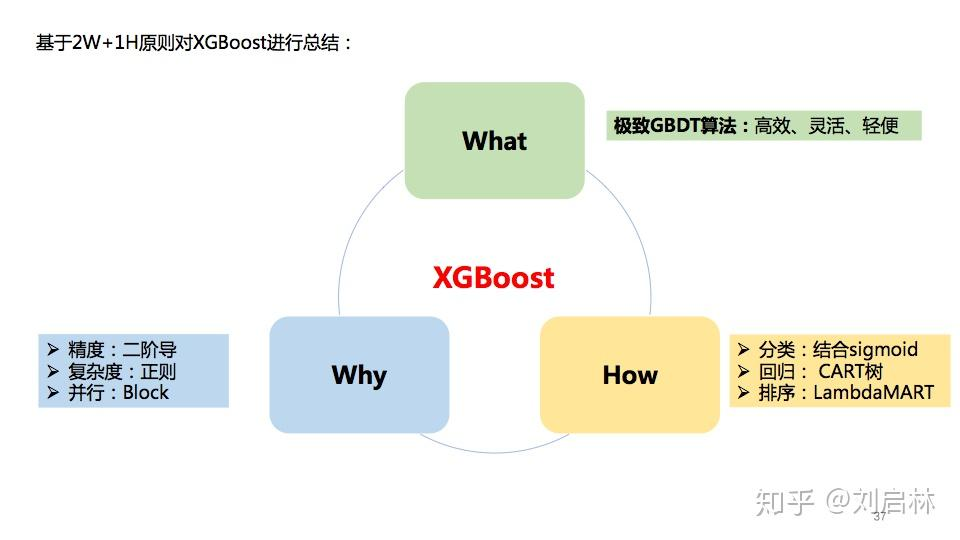
1. XGBoost算法的优势：

XGBoost算法是基于GDBT算法的工程化优化，主要优化有以下几个方面：

（1）损失函数采用二次泰勒展开进行逼近，准确性更高（GDBT是一阶导数）

（2）损失函数增加了正则项，避免过拟合

（3）用了block实现并行 + 还有lambdaMART的优化【没理解完】

2. 数学推导链接：

对于XGBoost的损失函数为什么是这个样子，树的划分判断原则公式为什么长这样，给一个推导链接，这里就不细说了（主要还是看的有些含混，，）

XGBoost的原理、公式推导、Python实现和应用 - 知乎

【AI夏令营】LightGBM的数学原理解读_哔哩哔哩_bilibili  （这个也讲了XGBoost）

3.  XGBoost和GDBT的实现过程上的区别在哪？

共同点：两者都是“Boosting”思想，每一轮训练一棵树来拟合 & 靠近 在该轮迭代过程中的 目标（对于GDBT来说是残差，对于XGBoost来说是目标函数，不过XGBoost迭代过程中也不涉及目标函数，直接根据目标函数进一步推导出划分树的公式 一步到位了），然后更新预测值，继续迭代。

不同点：XGBoost 看起来像是“数学版 GBDT”：直接使用 损失函数的梯度信息构造切分的“分裂增益” 和 “划分的叶子赋值公式” ，而 GBDT 是“经验主义”：靠残差（近似一阶信息）手动拟合。

对比如下：

GBDT 的建树逻辑：

• 残差 = label

• 使用标准的 CART 树：按属性和阈值划分数据

• 每个切分：计算左右子树的 MSE

• 挑选损失最小的切分点

• 递归建树

XGBoost的建树逻辑：

• 不用残差，不重构 label

• 每个样本 根据公式 计算出 对应的 一阶梯度 g_i 和二阶 h_i 

• 遍历属性 + 切分点，计算基于导数推导出的 增益公式

• 选最大增益的切分点

• 递归建树

4. XGBoost的建树过程：

 

5. XGBoost —— Split Gain 和叶子赋值的伪代码

 下面这段伪代码是高度简化版，展示 如何枚举特征切分点并计算每个分裂的增益（Gain）与叶子输出值（weight）

# 输入: 样本列表，每个样本包含 (g_i, h_i, feature_values)
# 超参数: lambda_ (正则化)，gamma (剪枝控制)

for feature in features:
    # 对特征值排序，配合 g_i, h_i 排序
    sorted_data = sort_by(feature)

    G_total = sum(g_i for g_i in sorted_data)
    H_total = sum(h_i for h_i in sorted_data)

    G_left, H_left = 0, 0

    for i in range(1, len(sorted_data)):
        g_i, h_i = sorted_data[i].g, sorted_data[i].h

        G_left += g_i
        H_left += h_i

        G_right = G_total - G_left
        H_right = H_total - H_left

        # 计算 Gain
        gain = 0.5 * (
            (G_left ** 2) / (H_left + lambda_) +
            (G_right ** 2) / (H_right + lambda_) -
            (G_total ** 2) / (H_total + lambda_)
        ) - gamma

        if gain > best_gain:
            best_gain = gain
            best_split = i
            best_feature = feature

# 最后叶子节点的输出值为：
leaf_weight = -G_j / (H_j + lambda_)

 

总结参考：

感谢大佬的无私分享，同时加入了一些自己的总结和理解，欢迎批评指正，相互交流~

决策树（ID3、C4.5、CART）的原理、Python实现、Sklearn可视化和应用 - 知乎