题目

逐题解析

13.1

知道p=83,q=41,h=2,g=4,x=57,y=77。

我看到答案，“消息M=56”的意思居然是杂凑值，也就是传统公式的H(M)。

选择k=23，那么r=(g^k mod p) mod q = 51 mod 41=10,s=k'(H(M)+xr) mod q=29

w=s' mod q=17,u1=(mw) mod q=9，u2=(rw) mod q=6，v=((g^u1*y^u2) mod p) mod q=10=r。

13.2

答：在DSA中，参数k泄露的后果：因为s=k-1(H(m)+xr)mod q，则除x外其余参数均为已知，上式由二元一次不定同余方程变为x的一元一次方程，私钥x即可求出，所以攻击者能够由此伪造任意消息的签名。

13.3

这一题居然是自定私钥。。。

13.4

答案：信息发送者使用一单向散列函数（HASH函数）对信息生成信息摘要；   信息发送者使用自己的私钥签名信息摘要；

信息发送者把信息本身和已签名的信息摘要一起发送出去；   信息接收者通过使用与信息发送者使用的同一个单向散列函数（HASH函数）对接收的信息本身生成新的信息摘要，再使用信息发送者的公钥对信息摘要进行验证，以确认信息发送者的身 份和信息是否被修改过。

13.5

在这题要分清楚，秘密发送是加密，用公钥，明确为签名，用私钥。

（1）在RSA公钥密码体制中，p=7,q=11得n=pq=77, φ(n)=(7-1)(11-1)=60。由ed ≡1 mod(φ(n))，即43e≡1 mod 60，利用扩展欧几里得算是得e=5。公开密钥为e，交给A保存的是私钥d。

（2）由（1）同理可得d=49。

（3）用A的公钥加密得密文c=6^85mod77=10。

（4）用A的私钥签名得签名s=md=68^41mod(77)=23，即<68，23>。

（5）验证m’=semodn是否与接收到的签名中的m相等，如果相等则为有效签名，否则是无效签名。

13.6

(1) 由公式可得：m = s^emodN = 8798^26959 mod 824737 = 123456

(2) 因为m’= s^emodN = 366314^26959 mod 824737 = 167058 = m，所以是有效的消息−签名对。

(3) m×m’的签名为：y = s×s’ mod N =4455587×229149 mod 824737 =75915。

推导：

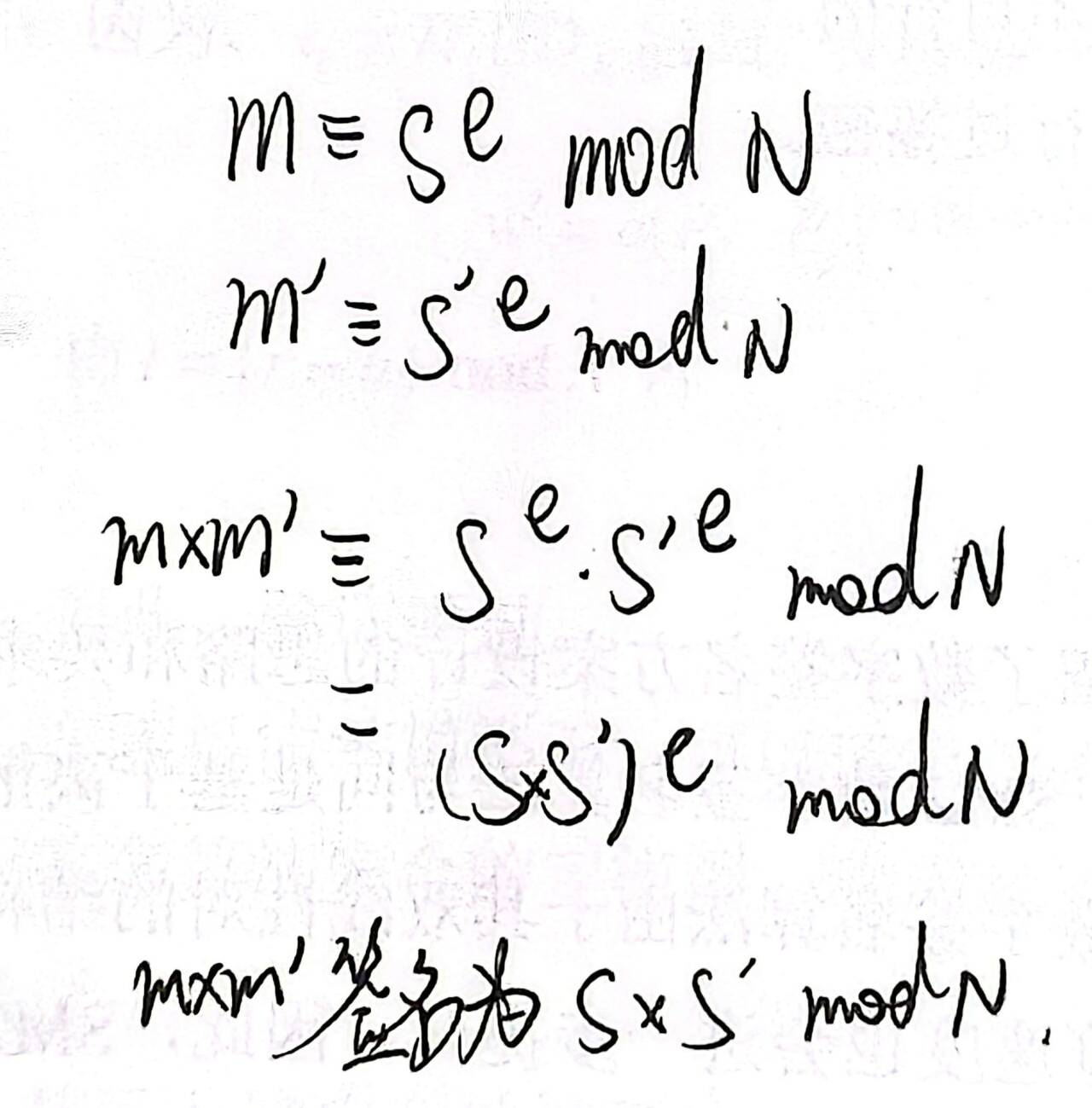
13.7