
一、考点分值占比与趋势分析
综合知识题分值统计表
| 年份 | 考题数量 | 总分值 | 分值占比 | 考察重点 |
|---|---|---|---|---|
| 2018 | 2 | 2 | 2.67% | 时间复杂度/稳定性判断 |
| 2019 | 3 | 3 | 4.00% | 算法特性对比分析 |
| 2020 | 2 | 2 | 2.67% | 空间复杂度要求 |
| 2021 | 1 | 1 | 1.33% | 算法稳定性判断 |
| 2022 | 3 | 3 | 4.00% | 综合特性应用 |
| 2023 | 2 | 2 | 2.67% | 时间复杂度计算 |
| 2024 | 2 | 2 | 2.67% | 分治策略应用 |
案例题分值统计表
| 年份 | 考题数量 | 总分值 | 分值占比 | 考察形式 | 考察重点 |
|---|---|---|---|---|---|
| 2018 | 0 | 0 | 0% | - | - |
| 2019 | 1 | 5 | 6.67% | 算法填空 | 归并排序实现 |
| 2020 | 1 | 5 | 6.67% | 流程图补全 | 快速排序过程 |
| 2021 | 0 | 0 | 0% | - | - |
| 2022 | 1 | 5 | 6.67% | 伪代码分析 | 堆排序原理 |
| 2023 | 1 | 5 | 6.67% | 复杂度计算 | 算法对比 |
| 2024 | 1 | 5 | 6.67% | 场景应用 | 稳定排序选择 |
趋势分析:排序算法在综合知识题中保持年均2-4%的稳定分值,重点考察时间复杂度、稳定性与空间复杂度的组合判断。案例题自2019年起呈现5年4考的规律,重点考核归并排序、堆排序的具体实现和分治策略应用,2024年新增场景应用题,强调算法选择能力。
二、真题考点深入挖掘
-
时间复杂度维度:
- 高频考查O(nlogn)级算法:堆排序(2018/2022)、归并排序(2019/2024)、快速排序(2020)的对比
- 特殊场景复杂度:冒泡排序最优情况O(n)(2021)、归并排序空间复杂度O(n)(2019)
-
稳定性维度:
- 必考稳定排序判定:归并排序(2018/2023)、冒泡排序(2021)的稳定性特征
- 不稳定算法陷阱:堆排序(2018/2022)、快速排序(2020)的不稳定特性
-
空间复杂度维度:
- 原地排序要求:堆排序O(1)(2018/2022)与快速排序递归栈空间(2020)对比
- 归并排序空间消耗:案例题多次要求分析其O(n)特性(2019/2023)
-
算法策略维度:
- 分治法应用:归并排序(2019)与快速排序(2020)的分治差异
- 堆结构应用:2022年案例题要求分析堆排序的二叉树结构特征
典型命题规律:组合型题目占比达60%,如"O(nlogn)+稳定"选归并排序(2018/2023),"O(nlogn)+原地"选堆排序(2018/2022)。
三、"wwwh"简述
是什么:排序算法是将数据元素按特定顺序排列的计算方法,核心指标包括时间复杂度、空间复杂度、稳定性。
为什么:
- 时间复杂度决定算法效率(如O(n²)级算法不适用大数据量)
- 空间复杂度影响内存消耗(如归并排序需要额外存储空间)
- 稳定性保障数据业务逻辑(如电商订单按时间+金额双排序)
怎么样:
- 比较类排序:通过元素比较确定次序(冒泡/快速/堆排序)
- 非比较类排序:通过数值特征确定次序(桶/基数排序,但不在当前考点范围)
如何做:
- 判断数据规模:小数据(n≤50)可用插入排序
- 分析稳定性需求:需要稳定则排除堆/快速排序
- 评估空间限制:内存紧张时选择原地排序(堆/快速)
- 综合决策:典型场景如"大数据+稳定"用归并排序,"大数据+内存受限"用堆排序
四、真题演练与解析
题目62(第1空)
题干:要求时间复杂度O(nlogn)且稳定,应选( )
选项:A.插入排序 B.堆排序 C.快速排序 D.归并排序
解析:
- 排除法:插入排序O(n²)不满足时间要求
- 堆排序和快速排序均为不稳定算法
- 归并排序同时满足O(nlogn)和稳定
答案:D
题目29
题干:稳定的排序算法是( )
选项:A.冒泡 B.快速 C.堆 D.简单选择
解析:
- 快速排序在划分时可能改变相等元素顺序
- 堆排序在调整堆结构时破坏稳定性
- 简单选择排序跨位置交换导致不稳定
答案:A
题目63(第2空)
题干:时间复杂度O(nlogn)且空间复杂度O(1)应选( )
解析:
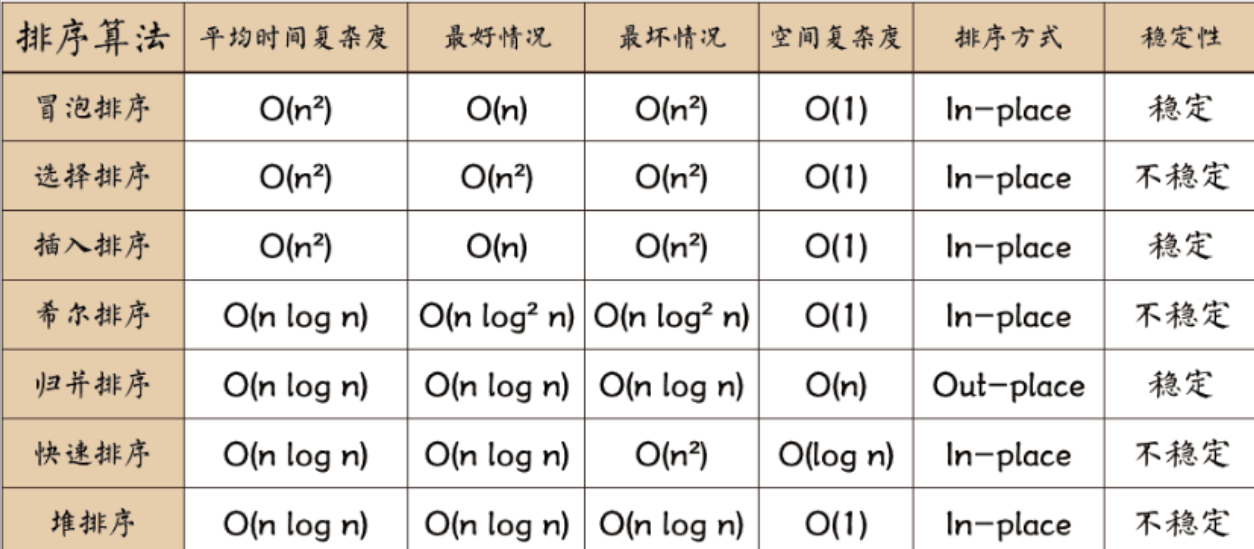
- 归并排序空间复杂度O(n)不符合
- 快速排序递归栈空间平均O(logn)
- 堆排序是唯一满足O(1)空间的O(nlogn)算法
答案:B
五、极简备考笔记
| 算法 | 时间复杂度 | 空间复杂度 | 稳定性 | 核心特征 |
|---|---|---|---|---|
| 冒泡排序 | O(n²)/O(n)最优 | O(1) | 稳定 | 相邻元素交换 |
| 快速排序 | O(nlogn)平均 | O(logn) | 不稳定 | 分治+基准元素 |
| 堆排序 | O(nlogn) | O(1) | 不稳定 | 完全二叉树结构 |
| 归并排序 | O(nlogn) | O(n) | 稳定 | 分治+额外存储空间 |
| 插入排序 | O(n²)/O(n)最优 | O(1) | 稳定 | 适合小规模数据 |
速记要点:
- 稳快空:稳定选归并,快速要空间,堆排省内存
- 时间三强:堆/快/归都是O(nlogn)
- 特殊场景:完全有序时冒泡排序最优
六、考点记忆顺口溜
堆快归并,时间优(时间复杂度最优)
空间堆快,原地走(堆排序和快速排序是原地排序)
稳定归并,冒泡有(稳定算法代表)
选择插入,分情况(根据数据规模选择)
分治策略,归并牛(归并排序采用分治法)
二叉树形,堆结构(堆排序的树形特征)
基准元素,快速排(快速排序的核心)
相邻交换,冒泡来(冒泡排序原理)
七、多角度解答
-
知识体系角度:
排序算法属于数据结构核心模块,与树结构(堆排序)、递归思想(快速排序)、分治策略(归并排序)紧密关联。掌握排序算法有助于理解更复杂的算法设计范式。 -
命题意图角度:
真题多设计组合条件(如"O(nlogn)+稳定")来考察考生对算法特性的综合理解能力,重点检测知识体系的完整性和应用能力。 -
解题技巧角度:
采用"条件拆解法":先处理时间复杂度→再筛选空间复杂度→最后验证稳定性。遇到案例题时,先识别算法特征(如出现merge()函数即为归并排序)。 -
错误防范角度:
高频易错点包括:
- 混淆快速排序最好/平均时间复杂度(都是O(nlogn))
- 忽视递归调用栈对空间复杂度的影响
- 误判插入排序的稳定性(实际是稳定算法)



















