【三维重建】【3DGS系列】【深度学习】3DGS的理论基础知识之如何形成高斯椭球

---

前言

在详细解析3DGS代码之前，首要任务是成功运行3DGS代码【理论基础及代码运行(win11下)解析参考教程】，后续学习才有意义。本博客讲解3DGS中如何形成高斯椭球，不涉及具体的模块代码。

---

参考：3D高斯的理论理解
参考：3d gaussian splatting全解 捏雪球

高斯函数

一维高斯

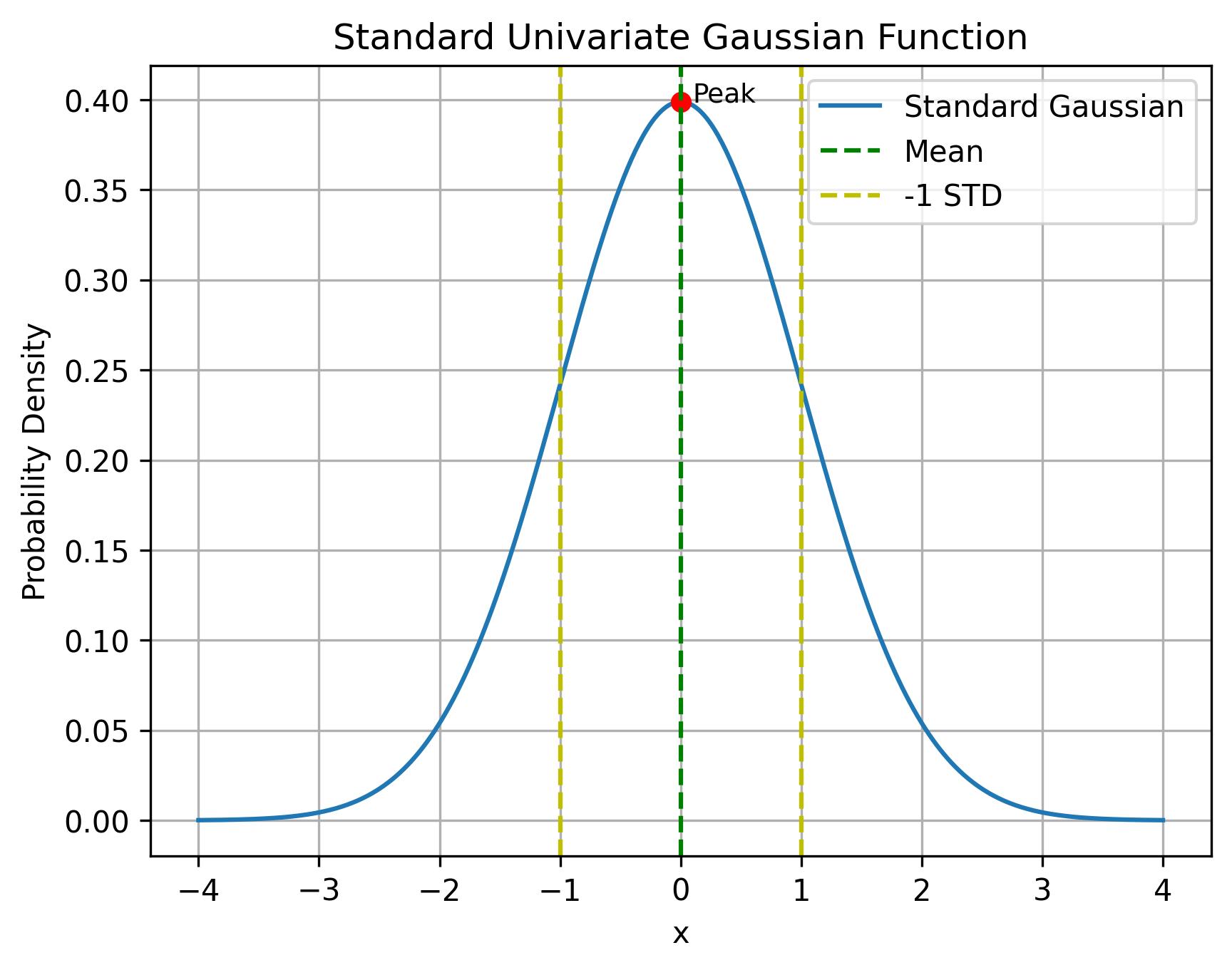
标准一维高斯函数：
$$f\left(x\right)=\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{x^2}{2}}$$

其中的$\sigma$表示高斯函数的方差， $\mu$表示高斯函数的均值；标准高斯函数的方差$\sigma$为1，均值$\mu$为0，概率密度之和为1。

import numpy as np
import matplotlib.pyplot as plt
# 定义高斯函数
def gaussian(x, mean=0, std=1):
    return (1 / (std * np.sqrt(2 * np.pi))) * np.exp(-((x - mean) ** 2) / (2 * std ** 2))

# 生成x轴数据
x = np.linspace(-4, 4, 500)

# 均值和标准差
mean = 0  # 均值 μ
std = 1   # 标准差 σ

# 计算对应y值
y = gaussian(x, mean, std)
# 绘制图形
plt.plot(x, y, label='Standard Gaussian')

# 在均值处标注峰值点
peak_y = gaussian(mean)
plt.plot(0, peak_y, 'ro')   # 红色圆圈标记
plt.text(0+0.1, peak_y, 'Peak', fontsize=9)

# 标注均值、±1σ, ±2σ, ±3σ的位置
plt.axvline(x=mean, color='g', linestyle='--', label='Mean')
plt.axvline(x=mean - std, color='y', linestyle='--', label='-1 STD')
plt.axvline(x=mean + std, color='y', linestyle='--')

# 添加图例
plt.legend()

# 图像标题与坐标轴标签
plt.title('Standard Univariate Gaussian Function')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.grid(True)

# 保存图像(文件名中包含均值和标准差)
filename = f'standard_gaussian_distribution.jpg'
plt.savefig(filename, dpi=300, bbox_inches='tight')
# 显示图像
plt.show()

不限制均值和方差，一维高斯函数：
$$f\left(x\right)=\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}$$

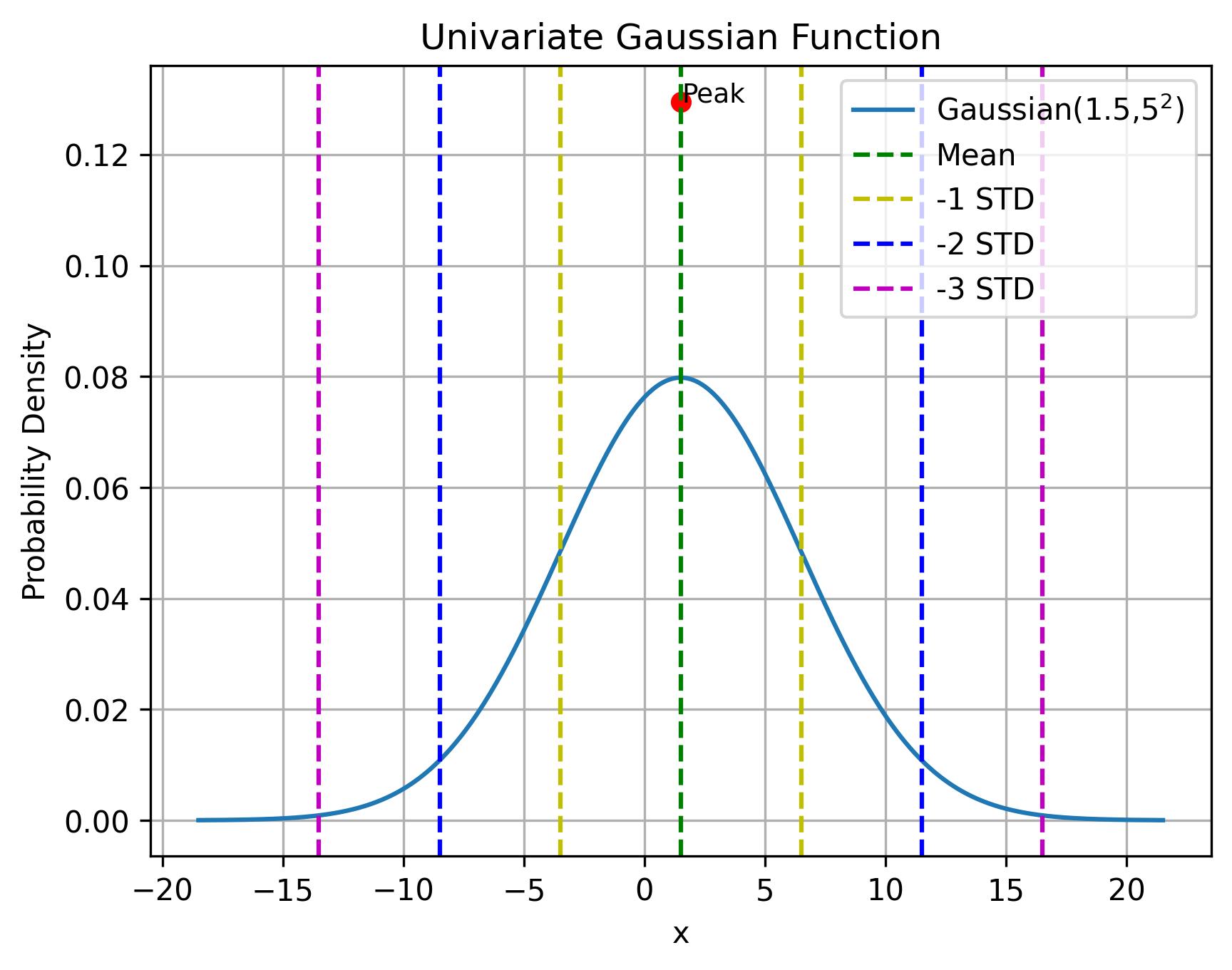
在数学上的意义为将标准高斯函数向右平移 $\mu$个单位，函数宽度延展了$\sigma$倍，分别决定了分布的位置和宽度，同时为了保证概率密度函数积分为1，$f\left(x\right)$ 的高度会下降，因为系数$\frac{1}{\sqrt{2\pi \sigma }}$。

import numpy as np
import matplotlib.pyplot as plt

# 定义高斯函数
def gaussian(x, mean=0, std=1):
    return (1 / (std * np.sqrt(2 * np.pi))) * np.exp(-((x - mean) ** 2) / (2 * std ** 2))


# 均值和标准差
mean = 1.5  # 均值 μ
std = 5   # 标准差 σ

# 生成x轴数据（根据均值和标准差适当调整范围）
x = np.linspace(mean - 4*std, mean + 4*std, 500)

# 计算对应y值
y = gaussian(x, mean, std)
# 绘制图形
plt.plot(x, y, label=f'Gaussian({mean},{std}$^2$)')

# 在均值处标注峰值点
peak_y = gaussian(mean)
plt.plot(mean, peak_y, 'ro')  # 红色圆圈标记
plt.text(mean + 0.05, peak_y, 'Peak', fontsize=9)

# 标注均值、±1σ, ±2σ, ±3σ的位置
plt.axvline(x=mean, color='g', linestyle='--', label='Mean')
plt.axvline(x=mean - std, color='y', linestyle='--', label='-1 STD')
plt.axvline(x=mean + std, color='y', linestyle='--')
plt.axvline(x=mean - 2*std, color='b', linestyle='--', label='-2 STD')
plt.axvline(x=mean + 2*std, color='b', linestyle='--')
plt.axvline(x=mean - 3*std, color='m', linestyle='--', label='-3 STD')
plt.axvline(x=mean + 3*std, color='m', linestyle='--')

# 添加图例
plt.legend()

# 图像标题与坐标轴标签
plt.title('Univariate Gaussian Function')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.grid(True)

# 保存图像(文件名中包含均值和标准差)
filename = f'gaussian_mu{mean}_sigma{std}.jpg'
plt.savefig(filename, dpi=300, bbox_inches='tight')
# 显示图像
plt.show()

多维高斯

1.$n$个服从正态分布且互不相关的独立变量$x={\left[x_1,x_2,...,x_n\right]}^T$，其均值为$\mu \left(x\right)={\left[{\mu }_1,{\mu }_2,...,{\mu }_n\right]}^T$，方差为$\sigma \left(x\right)={\left[{\sigma }_1,{\sigma }_2,...,{\sigma }_n\right]}^T$，根据概率论中的概率密度公式有：
$$f\left(x\right)=p\left(x_1,x_2,...,x_n\right)=p\left(x_1\right)p\left(x_2\right)...p\left(x_n\right)=\frac{1}{{\left(\sqrt{2\pi }\right)}^n{\sigma }_1{\sigma }_1...{\sigma }_n}{e}^{-\frac{{\left(x_1-{\mu }_1\right)}^2}{2{{\sigma }_1}^2}-\frac{{\left(x_2-{\mu }_2\right)}^2}{2{{\sigma }_2}^2}...-\frac{{\left(x_n-{\mu }_n\right)}^2}{2{{\sigma }_n}^2}}$$

• 将$\frac{{\left(x_1-{\mu }_1\right)}^2}{2{{\sigma }_1}^2}+\frac{{\left(x_2-{\mu }_2\right)}^2}{2{{\sigma }_2}^2}...+\frac{{\left(x_n-{\mu }_n\right)}^2}{2{{\sigma }_n}^2}$分解表示：
  $$\left[x_1-{\mu }_1,x_2-{\mu }_2...x_n-{\mu }_n\right]\left[\begin{array}{cccc}\frac{1}{{\sigma }_1^2}& 0& ....& 0\\ 0& \frac{1}{{\sigma }_2^2}& ....& 0\\ ....& ....& ....& ....\\ 0& 0& ....& \frac{1}{{\sigma }_n^2}\end{array}\right]{\left[x_1-{\mu }_1,x_2-{\mu }_2...x_n-{\mu }_n\right]}^T$$
  用$x-{\mu }_x$表示${\left[x_1-{\mu }_1,x_2-{\mu }_2...x_n-{\mu }_n\right]}^T$；用协方差矩阵$\Sigma$表示 $\left[\begin{array}{cccc}{\sigma }_1^2& 0& ....& 0\\ 0& {\sigma }_2^2& ....& 0\\ ....& ....& ....& ....\\ 0& 0& ....& {\sigma }_n^2\end{array}\right]$，则进一步简化为${\left(x-{\mu }_x\right)}^T(\Sigma {)}^{-1}\left(x-{\mu }_x\right)$。
• $\Sigma$行列式为$\left|\Sigma \right|={\sigma }_1^2{\sigma }_2^2....{\sigma }_n^2$，因此${\left|\Sigma \right|}^{\frac{1}{2}}={\sigma }_1{\sigma }_2....{\sigma }_n$。

因此多维正态高斯分布函数：
$$f\left(x\right)=\frac{1}{{\left(\sqrt{2\pi }\right)}^n{\left|\Sigma \right|}^{\frac{1}{2}}}{e}^{-\frac{{\left(x-{\mu }_x\right)}^T{(\Sigma )}^{-1}\left(x-{\mu }_x\right)}{2}}$$

2.$n$个服从正态分布且的随机变量$x={\left[x_1,x_2,...,x_n\right]}^T$，其均值为$\mu \left(x\right)={\left[{\mu }_1,{\mu }_2,...,{\mu }_n\right]}^T$，方差为$\sigma \left(x\right)={\left[{\sigma }_1,{\sigma }_2,...,{\sigma }_n\right]}^T$，还需要一个协方差矩阵$\Sigma$来描述变量之间的相关性。多维正态高斯分布函数依旧是：
$$f\left(x\right)=\frac{1}{{\left(\sqrt{2\pi }\right)}^n{\left|\Sigma \right|}^{\frac{1}{2}}}{e}^{-\frac{{\left(x-{\mu }_x\right)}^T{(\Sigma )}^{-1}\left(x-{\mu }_x\right)}{2}}$$
协方差矩阵同样是一个$\mathrm{n}\times \mathrm{n}$的矩阵，其元素${\Sigma }_{ij}$表示第$i$个随机变量与第$j$个随机变量之间的协方差：
$$\Sigma =\left[\begin{array}{cccc}{\sigma }_1^2& {\sigma }_{12}& ....& {\sigma }_{1n}\\ {\sigma }_{21}& {\sigma }_2^2& ....& {\sigma }_{2n}\\ ....& ....& ....& ....\\ {\sigma }_{n1}& {\sigma }_{n2}& ....& {\sigma }_n^2\end{array}\right]$$
如果${\Sigma }_{ij}={\sigma }_{ij}=0$ 说明第$i$个变量和第$j$个变量之间没有线性相关性，$n$个服从正态分布且互不相关的独立变量即是这种情况，互相都没有线性相关性；
如果${\Sigma }_{ij}={\sigma }_{ij}\ne 0$则说明第$i$个变量和第$j$个变量之间存在线性相关性。

---

椭球

基本定义

在坐标系中椭球方程表示为：
$$\frac{{\left(x-x_0\right)}^2}{a^2}+\frac{{\left(y-y_0\right)}^2}{b^2}+\frac{{\left(z-z_0\right)}^2}{c^2}=1$$
椭球的中心位于空间中的某一点$\left(x_0,y_0,z_0\right)$，其中，$a$、$b$和$c$分别是椭球沿$x$、$y$和$z$轴方向的半轴长度。如果 $a=b=c$，则该图形是一个球体。
当椭球中心点位于坐标原点$(0,0,0)$时，标准椭球(中心位于原点且轴与坐标轴对齐的椭球)的方程可以表示为：
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$$

一般二次形式

用二次方程来表示三维空间中任意位置、任意方向的椭球。这种形式可以涵盖椭球的中心不在原点、主轴不与坐标轴对齐的情况。
主轴与坐标轴对齐的情况： 通过展开椭球方程，将其转化为一个一般的二次曲面形式(即包含$x^2$ 、$y^2$、$z^2$、一次项和常数项的形式)：

• 展开平方项：
  $$\frac{{\left(x-x_0\right)}^2}{a^2}=\frac{x^2-2x{x}_0+{x_0}^2}{a^2}$$
  $$\frac{{\left(y-y_0\right)}^2}{b^2}=\frac{y^2-2y{y}_0+{y_0}^2}{b^2}$$
  $$\frac{{\left(z-z_0\right)}^2}{c^2}=\frac{z^2-2z{z}_0+{z_0}^2}{c^2}$$
• 整理为一般二次形式：
  $$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{b^2}-\frac{2x{x}_0}{a^2}-\frac{2y{y}_0}{b^2}-\frac{2z{z}_0}{c^2}+(\frac{{x_0}^2}{a^2}+\frac{{y_0}^2}{b^2}+\frac{{z_0}^2}{c^2})=1$$

一般二次形式的格式如下：
$$A{x}^2+B{y}^2+C{z}^2+Dx+Ey+Fz+G=1$$
椭球的中心位于空间中的某一点$\left(x_0,y_0,z_0\right)$，对应地：$A=\frac{1}{a^2}$；$B=\frac{1}{b^2}$；$C=\frac{1}{c^2}$；$D=\frac{2x_0}{a^2}$；$E=\frac{2x_0}{b^2}$；$F=\frac{2x_0}{z^2}$；$G=(\frac{{x_0}^2}{a^2}+\frac{{y_0}^2}{b^2}+\frac{{z_0}^2}{c^2})$。
当椭球中心点位于坐标原点$(0,0,0)$时：
$$A{x}^2+B{y}^2+C{z}^2=1$$
主轴不与坐标轴对齐的情况(常见情形)： 椭球中心点$({\mathrm{x}}_0,{\mathrm{y}}_0,{\mathrm{z}}_0)$平移到原点，然后椭球经过绕$z$轴旋转$\alpha$，绕$y$轴旋转$\beta$，绕$x$轴旋转$\gamma$。

• 中心点$({\mathrm{x}}_0,{\mathrm{y}}_0,{\mathrm{z}}_0)$平移到坐标原点：
  $$\begin{array}{l}x\prime =x-x_0\\ y\prime =y-y_0\\ z\prime =z-z_0\end{array}$$
• 绕$z$轴旋转$\alpha$，旋转矩阵$R_{\mathrm{z}}\left(\alpha \right)$：
  $$R_{\mathrm{z}}\left(\alpha \right)=\left[\begin{array}{ccc}\cos \alpha & -\sin \alpha & 0\\ \sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right]$$
  旋转后的坐标$(\mathrm{x}\prime \prime ,\mathrm{y}\prime \prime ,\mathrm{z}\prime \prime )$由坐标$(\mathrm{x}\prime ,\mathrm{y}\prime ,\mathrm{z}\prime )$计算得出：
  $$\left[\begin{array}{c}x\prime \prime \\ y\prime \prime \\ z\prime \prime \end{array}\right]=R_x\left(\alpha \right)\left[\begin{array}{c}x\prime \\ x\prime \\ x\prime \end{array}\right]$$
  其中$(\mathrm{x}\prime \prime ,\mathrm{y}\prime \prime ,\mathrm{z}\prime \prime )$的值分别为：
  $$\begin{array}{l}x\prime \prime =x\prime \cos \alpha -y\prime \sin \alpha \\ y\prime \prime =x\prime \sin \alpha +y\prime \cos \alpha \\ z\prime \prime =z\prime \end{array}$$
• 绕$y$轴旋转$\beta$，旋转矩阵$R_y\left(\beta \right)$：
  $$R_y\left(\beta \right)=\left[\begin{array}{ccc}\cos \beta & 0& \sin \beta \\ 0& 1& 0\\ -\sin \beta & 0& \cos \beta \end{array}\right]$$
  旋转后的坐标$(\mathrm{x}\prime \prime \prime ,\mathrm{y}\prime \prime \prime ,\mathrm{z}\prime \prime \prime )$由原始坐标$(\mathrm{x}\prime \prime ,\mathrm{y}\prime \prime ,\mathrm{z}\prime \prime )$计算得出：
  $$\left[\begin{array}{c}x\prime \prime \prime \\ y\prime \prime \prime \\ z\prime \prime \prime \end{array}\right]=R_y\left(\beta \right)\left[\begin{array}{c}x\prime \prime \\ y\prime \prime \\ z\prime \prime \end{array}\right]$$
  其中$(\mathrm{x}\prime \prime \prime ,\mathrm{y}\prime \prime \prime ,\mathrm{z}\prime \prime \prime )$的值分别为：
  $$\begin{array}{l}x\prime \prime \prime =x\prime \prime \cos \beta +z\prime \prime \sin \beta =(x\prime \cos \alpha -y\prime \sin \alpha )\cos \beta +z\prime \sin \beta \\ y\prime \prime \prime =y\prime \prime =x\prime \sin \alpha +y\prime \cos \alpha \\ z\prime \prime \prime =-x\prime \prime \sin \beta +z_1\cos \beta =-(x\prime \cos \alpha -y\prime \sin \alpha )\sin \beta +z\prime \cos \beta \end{array}$$
• 绕$x$轴旋转$\gamma$，旋转矩阵$R_z\left(\gamma \right)$：
  $$R_z\left(\gamma \right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \gamma & -\sin \gamma \\ 0& \sin \gamma & \cos \gamma \end{array}\right]$$
  旋转后的坐标$(\mathrm{x}\prime \prime \prime \prime ,\mathrm{y}\prime \prime \prime \prime ,\mathrm{z}\prime \prime \prime \prime )$由原始坐标$(\mathrm{x}\prime \prime \prime ,\mathrm{y}\prime \prime \prime ,\mathrm{z}\prime \prime \prime )$计算得出：
  $$\left[\begin{array}{c}x\prime \prime \prime \prime \\ y\prime \prime \prime \prime \\ z\prime \prime \prime \prime \end{array}\right]=R_z\left(\gamma \right)\left[\begin{array}{c}x\prime \prime \prime \\ y\prime \prime \prime \\ z\prime \prime \prime \end{array}\right]$$
  其中$(\mathrm{x}\prime \prime \prime \prime ,\mathrm{y}\prime \prime \prime \prime ,\mathrm{z}\prime \prime \prime \prime )$的值分别为：
  $$\begin{array}{l}x\prime \prime \prime \prime =x\prime \prime \prime =(x\prime \cos \alpha -y\prime \sin \alpha )\cos \beta +z\prime \sin \beta \\ y\prime \prime \prime \prime =y\prime \prime \prime \cos \gamma -z\prime \prime \prime \sin \gamma =(x\prime \sin \alpha +y\prime \cos \alpha )\cos \gamma -(-(x\prime \cos \alpha -y\prime \sin \alpha )\sin \beta +z\prime \cos \beta )\sin \gamma \\ z\prime \prime \prime \prime =y\prime \prime \prime \sin \gamma +z\prime \prime \prime \cos \gamma =(x\prime \sin \alpha +y\prime \cos \alpha )\sin \gamma +(-(x\prime \cos \alpha -y\prime \sin \alpha )\sin \beta +z\prime \cos \beta )\cos \gamma \end{array}$$
  将坐标$(\mathrm{x}\prime ,\mathrm{y}\prime ,\mathrm{z}\prime )$转化成$(\mathrm{x},\mathrm{y},\mathrm{z})$：
  $$\begin{array}{l}x\prime \prime \prime \prime =((x-x_0)\cos \alpha -(y-y_0)\sin \alpha )\cos \beta +(z-z_0)\sin \beta \\ y\prime \prime \prime \prime =((x-x_0)\sin \alpha +(y-y_0)\cos \alpha )\cos \gamma -(-((x-x_0)\cos \alpha -(y-y_0)\sin \alpha )\sin \beta +(z-z_0)\cos \beta )\sin \gamma \\ z\prime \prime \prime \prime =((x-x_0)\sin \alpha +(y-y_0)\cos \alpha )\sin \gamma +(-((x-x_0)\cos \alpha -(y-y_0)\sin \alpha )\sin \beta +(z-z_0)\cos \beta )\cos \gamma \end{array}$$

将$(\mathrm{x}\prime \prime \prime \prime ,\mathrm{y}\prime \prime \prime \prime ,\mathrm{z}\prime \prime \prime \prime )$代入标准椭球方程：
$$\frac{x\prime \prime \prime {\prime }^2}{a^2}+\frac{y\prime \prime \prime {\prime }^2}{b^2}+\frac{z\prime \prime \prime {\prime }^2}{c^2}=1$$
总的旋转矩阵为：
$$R=R_x\left(\gamma \right)R_y\left(\beta \right)R_z\left(\alpha \right)=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]=\left[\begin{array}{ccc}\cos \alpha \cos \beta & \cos \alpha \sin \beta \sin \gamma -\sin \alpha \cos \gamma & \cos \alpha \sin \beta \cos \gamma +\sin \alpha \sin \gamma \\ \sin \alpha \cos \beta & \sin \alpha \sin \beta \sin \gamma +\cos \alpha \cos \gamma & \sin \alpha \sin \beta \cos \gamma -\cos \alpha \sin \gamma \\ -\sin \beta & \cos \beta \sin \gamma & -\cos \beta \cos \gamma \end{array}\right]$$
展开并整理此方程，得到一般二次形式：
$$A{\mathrm{x}}^2+B{y}^2+C{z}^2+Dxy+Exz+Fyz++Gx+Hy+Iz+J=0$$
二次项系数：
$$\begin{array}{l}A=\frac{r_{11}^2}{a^2}+\frac{r_{21}^2}{b^2}+\frac{r_{31}^2}{c^2}\\ B=\frac{r_{12}^2}{a^2}+\frac{r_{22}^2}{b^2}+\frac{r_{32}^2}{c^2}\\ C=\frac{r_{13}^2}{a^2}+\frac{r_{23}^2}{b^2}+\frac{r_{33}^2}{c^2}\end{array}$$
交叉项系数：
$$\begin{array}{l}D=2(\frac{r_{11}{r}_{12}}{a^2}+\frac{r_{21}{r}_{22}}{b^2}+\frac{r_{31}{r}_{32}}{c^2})\\ E=2(\frac{r_{11}{r}_{13}}{a^2}+\frac{r_{21}{r}_{23}}{b^2}+\frac{r_{31}{r}_{33}}{c^2})\\ F=2(\frac{r_{12}{r}_{13}}{a^2}+\frac{r_{22}{r}_{23}}{b^2}+\frac{r_{32}{r}_{33}}{c^2})\end{array}$$
一次项系数：
$$\begin{array}{l}G=-2\left(\frac{x_0}{a^2}{r}_{11}^2+\frac{y_0}{b^2}{r}_{21}^2+\frac{z_0}{c^2}{r}_{31}^2+\frac{x_0}{b^2}(2r_{11}{r}_{21})+\frac{x_0}{c^2}(2r_{11}{r}_{31})+\frac{y_0}{a^2}(2r_{11}{r}_{21})+\frac{y_0}{c^2}(2r_{21}{r}_{31})+\frac{z_0}{a^2}(2r_{11}{r}_{31})+\frac{z_0}{b^2}(2r_{21}{r}_{31})\right)\\ H=-2\left(\frac{x_0}{a^2}{r}_{12}^2+\frac{y_0}{b^2}{r}_{22}^2+\frac{z_0}{c^2}{r}_{32}^2+\frac{x_0}{b^2}(2r_{12}{r}_{22})+\frac{x_0}{c^2}(2r_{12}{r}_{32})+\frac{y_0}{a^2}(2r_{12}{r}_{22})+\frac{y_0}{c^2}(2r_{22}{r}_{32})+\frac{z_0}{a^2}(2r_{12}{r}_{32})+\frac{z_0}{b^2}(2r_{22}{r}_{32})\right)\\ G=-2\left(\frac{x_0}{a^2}{r}_{13}^2+\frac{y_0}{b^2}{r}_{23}^2+\frac{z_0}{c^2}{r}_{33}^2+\frac{x_0}{b^2}(2r_{13}{r}_{23})+\frac{x_0}{c^2}(2r_{13}{r}_{33})+\frac{y_0}{a^2}(2r_{13}{r}_{23})+\frac{y_0}{c^2}(2r_{23}{r}_{33})+\frac{z_0}{a^2}(2r_{13}{r}_{33})+\frac{z_0}{b^2}(2r_{23}{r}_{33})\right)\end{array}$$
常数项:
$$J=\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}+\frac{z_0^2}{c^2}-1$$

---

3D高斯椭球

3D高斯与椭球的关系

回顾了多维高斯和椭球的基础知识，本小节终于到了解释3D高斯明明是个分布，为什么可以是个椭球。

三维正态分布的概率密度函数可以表示为：
$$f\left([x,y,z]\right)=\frac{1}{{\left(\sqrt{2\pi }\right)}^3{\left|\Sigma \right|}^{\frac{1}{2}}}{e}^{-\frac{{\left(x-{\mu }_x\right)}^T{(\Sigma )}^{-1}\left(x-{\mu }_x\right)}{2}}$$
$\mu$是均值向量，${\mu }_1$、${\mu }_2$、${\mu }_3$分别是$x$、$y$、$z$的均值：
$$\mu =\left[\begin{array}{c}{\mu }_1\\ {\mu }_2\\ {\mu }_3\end{array}\right]$$
$\Sigma$是协方差矩阵，它是一个$3\times 3$的矩阵，${\sigma }_1^2$、${\sigma }_2^2$、${\sigma }_3^2$分别是$x$、$y$、$z$的方差，${\sigma }_{12}$、${\sigma }_{13}$、${\sigma }_{23}$分别是 $x$与$y$、$x$与$z$、$y$与$z$的协方差：
$$\Sigma =\left[\begin{array}{ccc}{\sigma }_1^2& {\sigma }_{12}& {\sigma }_{13}\\ {\sigma }_{21}& {\sigma }_2^2& {\sigma }_{23}\\ {\sigma }_{31}& {\sigma }_{32}& {\sigma }_3^2\end{array}\right]$$
其中指数部分展开为：
$${\left(x-{\mu }_x\right)}^T(\Sigma {)}^{-1}\left(x-{\mu }_x\right)=\frac{{\left(x-{\mu }_1\right)}^2}{{\sigma }_1^2}+\frac{{\left(y-{\mu }_2\right)}^2}{{\sigma }_2^2}+\frac{{\left(z-{\mu }_3\right)}^2}{{\sigma }_3^2}-\frac{2{\sigma }_{12}\left(x-{\mu }_1\right)\left(y-{\mu }_2\right)}{{\sigma }_1{\sigma }_2}-\frac{2{\sigma }_{13}\left(x-{\mu }_1\right)\left(\left(z-{\mu }_3\right)\right)}{{\sigma }_1{\sigma }_3}-\frac{2{\sigma }_{23}\left(y-{\mu }_2\right)\left(\left(z-{\mu }_3\right)\right)}{{\sigma }_2{\sigma }_3}$$
因此，公式展开为：
$$f\left([x,y,z]\right)=\frac{1}{{\left(\sqrt{2\pi }\right)}^3{\left|\Sigma \right|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}\left[\frac{{\left(x-{\mu }_1\right)}^2}{{\sigma }_1^2}+\frac{{\left(y-{\mu }_2\right)}^2}{{\sigma }_2^2}+\frac{{\left(z-{\mu }_3\right)}^2}{{\sigma }_3^2}-\frac{2{\sigma }_{12}\left(x-{\mu }_1\right)\left(y-{\mu }_2\right)}{{\sigma }_1{\sigma }_2}-\frac{2{\sigma }_{13}\left(x-{\mu }_1\right)\left(\left(z-{\mu }_3\right)\right)}{{\sigma }_1{\sigma }_3}-\frac{2{\sigma }_{23}\left(y-{\mu }_2\right)\left(\left(z-{\mu }_3\right)\right)}{{\sigma }_2{\sigma }_3}\right]}$$
对于一个确定的三维高斯函数，其概率密度函数的取值范围是有限的，最大值出现在均值点$\mathrm{x}=\mu$，当 $x$远离$\mu$时函数值趋近于0。因此对应的${\left(x-{\mu }_x\right)}^T(\Sigma {)}^{-1}\left(x-{\mu }_x\right)$取值范围也是从0到一个具体的、有限的数值。当${\left(x-{\mu }_x\right)}^T(\Sigma {)}^{-1}\left(x-{\mu }_x\right)=\mathrm{constant}$时，即在取值范围内随机取某个值$constant$，可以定义某一个椭球面：
$$\frac{{\left(x-{\mu }_1\right)}^2}{{\sigma }_1^2}+\frac{{\left(y-{\mu }_2\right)}^2}{{\sigma }_2^2}+\frac{{\left(z-{\mu }_3\right)}^2}{{\sigma }_3^2}-\frac{2{\sigma }_{12}\left(x-{\mu }_1\right)\left(y-{\mu }_2\right)}{{\sigma }_1{\sigma }_2}-\frac{2{\sigma }_{13}\left(x-{\mu }_1\right)\left(\left(z-{\mu }_3\right)\right)}{{\sigma }_1{\sigma }_3}-\frac{2{\sigma }_{23}\left(y-{\mu }_2\right)\left(\left(z-{\mu }_3\right)\right)}{{\sigma }_2{\sigma }_3}=\mathrm{constant}$$
因为展开整理，可以得到椭圆的一般二次形式：
$$A{\mathrm{x}}^2+B{y}^2+C{z}^2+Dxy+Exz+Fyz++Gx+Hy+Iz+J=0$$
因此${\left(x-{\mu }_x\right)}^T(\Sigma {)}^{-1}\left(x-{\mu }_x\right)$在其取值范围内可以构成无数个椭圆面，大椭球面套小椭球面，共同组成了一个实心椭球。每个椭圆面都可以计算出对应的概论密度值$f\left([x,y,z]\right)=\mathrm{constant}$，即椭球面上的所有坐标点的概论密度值。

各向同性(Isotropic)和各向异性(Anisotropic)

进一步深入探讨各向同性和 各向异性在 3D高斯分布中的数学形式以及几何表现。
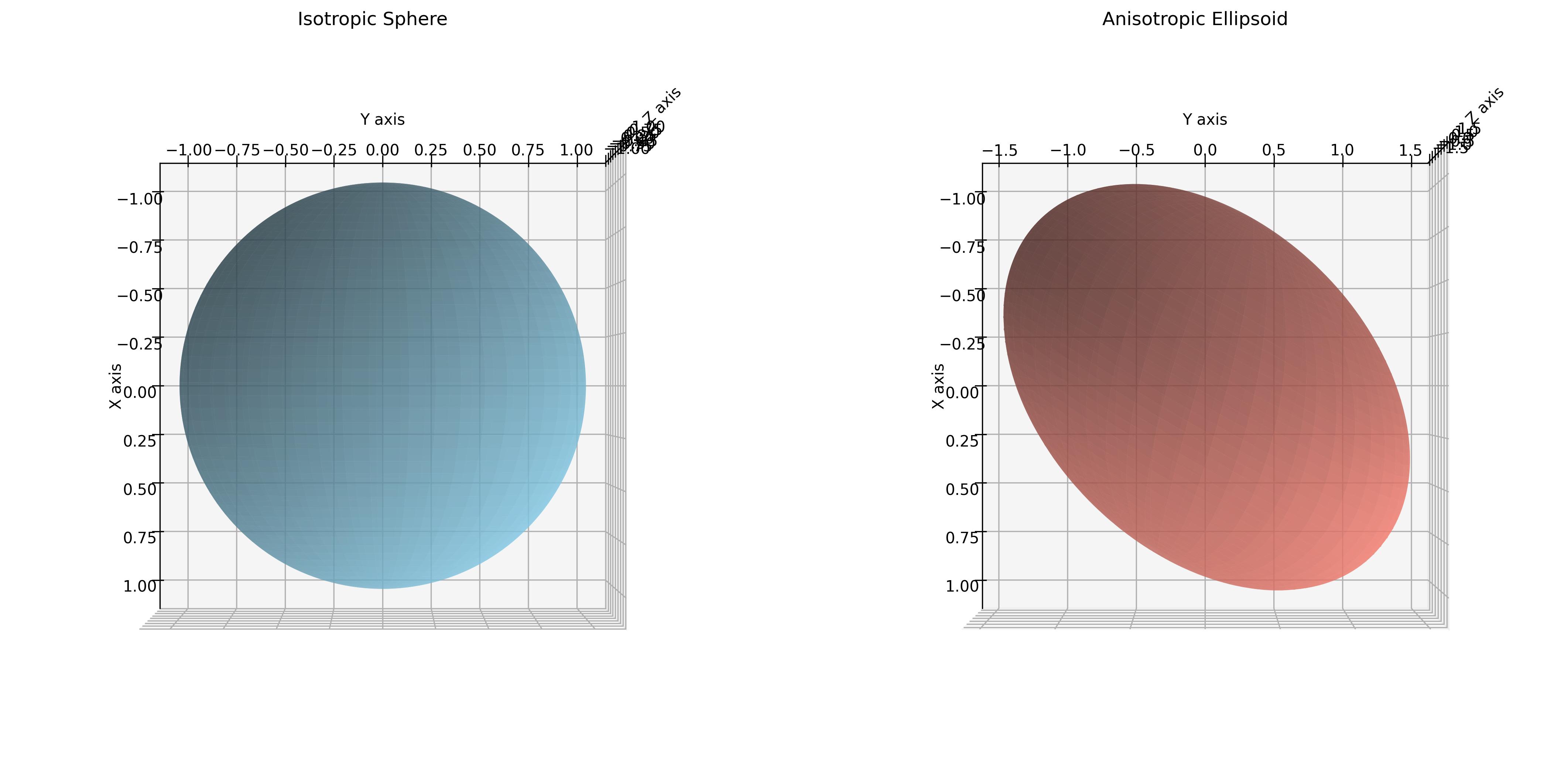
各向同性高斯分布： 指在所有方向上具有相同的性质，数据在各个方向上的扩展程度(方差)相同，协方差为0，协方差矩阵：
$$\Sigma =\left[\begin{array}{ccc}{\sigma }^2& 0& 0\\ 0& {\sigma }^2& 0\\ 0& 0& {\sigma }^2\end{array}\right]$$
三个维度之间无相关性(协方差为0)，且方差一致。 对应的高斯分布在三维空间中呈现为一个球形。
各向异性高斯分布： 表示在不同方向上性质不同，数据在不同方向上的扩展程度(方差)不同，协方差可能不为0，协方差矩阵更一般化：
$$\Sigma =\left[\begin{array}{ccc}{\sigma }_1^2& {\sigma }_{12}& {\sigma }_{13}\\ {\sigma }_{21}& {\sigma }_2^2& {\sigma }_{23}\\ {\sigma }_{31}& {\sigma }_{32}& {\sigma }_3^2\end{array}\right]$$
三个维度之间可能有相关性(协方差不为0)，且方差互不一致。对应的高斯分布在三维空间中呈现为一个椭球体，即沿不同主轴方向拉伸或压缩。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def plot_ellipsoid(ax, mean, cov, color='blue', n_points=100):
    """
    在给定的axes上绘制一个基于协方差矩阵的椭球。
    """
    # 生成单位球面点
    u = np.linspace(0, 2 * np.pi, n_points)
    v = np.linspace(0, np.pi, n_points)
    x = np.outer(np.cos(u), np.sin(v))
    y = np.outer(np.sin(u), np.sin(v))
    z = np.outer(np.ones_like(u), np.cos(v))

    # 协方差矩阵特征分解
    eigvals, eigvecs = np.linalg.eigh(cov)

    # 按特征值大小排序（从大到小）
    idx = np.argsort(eigvals)[::-1]
    eigvals = eigvals[idx]
    eigvecs = eigvecs[:, idx]

    # 构建缩放矩阵
    scale_matrix = np.diag(np.sqrt(eigvals))  # 取平方根得到标准差

    # 将单位球变换为椭球
    for i in range(len(x)):
        points = np.column_stack([x[i], y[i], z[i]])
        transformed = points @ (scale_matrix @ eigvecs.T) + mean
        x[i], y[i], z[i] = transformed[:, 0], transformed[:, 1], transformed[:, 2]

    # 绘制椭球
    ax.plot_surface(x, y, z, color=color, alpha=0.6, linewidth=0, antialiased=True)

# 创建图形和子图
fig = plt.figure(figsize=(15, 7))

# 各向同性椭球（球体）
ax1 = fig.add_subplot(121, projection='3d')
mean_iso = [0, 0, 0]
cov_iso = np.eye(3)
plot_ellipsoid(ax1, mean_iso, cov_iso, color='skyblue')

# 设置坐标轴标签
ax1.set_xlabel('X axis')
ax1.set_ylabel('Y axis')
ax1.set_zlabel('Z axis')
ax1.set_title('Isotropic Sphere')

# 调整视角以正对Z轴
ax1.view_init(elev=90, azim=0)

# 各向异性椭球
ax2 = fig.add_subplot(122, projection='3d')
mean_aniso = [0, 0, 0]
cov_aniso = np.array([[1, 0.5, 0.3],
                      [0.5, 2, 0.4],
                      [0.3, 0.4, 3]])
plot_ellipsoid(ax2, mean_aniso, cov_aniso, color='salmon')

# 设置坐标轴标签
ax2.set_xlabel('X axis')
ax2.set_ylabel('Y axis')
ax2.set_zlabel('Z axis')
ax2.set_title('Anisotropic Ellipsoid')

# 调整视角以正对Z轴
ax2.view_init(elev=90, azim=0)

plt.tight_layout()
plt.savefig("gaussian_distribution_visualizer.jpg", dpi=300, bbox_inches='tight')
plt.show()

---

总结

尽可能简单、详细的介绍了高斯椭球的形成原理。