蚁群算法赋能生鲜配送：MATLAB 实现多约束路径优化

在生鲜农产品配送中，如何平衡运输效率与成本控制始终是行业难题。本文聚焦多目标路径优化，通过 MATLAB 实现蚁群算法，解决包含载重限制、时间窗约束、冷藏货损成本的复杂配送问题。代码完整复现了从数据生成到路径优化的全流程，助力物流从业者提升配送效能。

一、问题建模：多维成本与约束的精准刻画

1. 目标函数：五维成本最小化

总成本 = 固定成本 + 运输成本 + 冷藏成本 + 货损成本 + 时间窗惩罚成本

固定成本：每辆车启用产生的固定费用（v_fixed）
运输成本：与行驶距离正相关（v_dist为单位距离成本）
冷藏成本：包含运输过程（P1）和卸货时间（P2）的冷链维护成本
货损成本：基于到达时间的指数衰减模型（alpha1控制损耗速率）
时间窗惩罚：提前（V3）或延迟（V4）送达的线性惩罚

2. 核心约束

载重限制：单车载重不超过容量Q
距离限制：单轮行驶距离不超过L（含往返配送中心）
时间窗约束：必须在客户指定时间窗[e_j, l_j]内送达

二、数据生成：从模糊需求到精确建模

1. 客户与环境参数

rng(1);               % 固定随机种子确保复现性  
N = 50;               % 50个客户点  
coords = rand(N+1,2)*100; coords(1,:) = [0,0];  % 配送中心坐标(0,0)

客户坐标随机生成，配送中心固定于原点
需求采用三角模糊数处理：[q1,q2,q3]通过加权平均（权重[1/6,4/6,1/6]）转化为确定需求D_i，增强数据鲁棒性

2. 成本与车辆参数

K = 10;    % 最大可用车辆数  
Q = 100;   % 单车最大载重  
L = 300;   % 单车最大行驶距离  
speed = 1; % 车辆行驶速度（距离/时间单位）

定义车辆物理约束与成本系数，支持灵活调整业务场景

三、蚁群算法：仿生优化的核心逻辑

1. 算法参数配置

numAnts = 20;   % 蚂蚁数量  
maxIter  = 200; % 最大迭代次数  
rho      = 0.1; % 信息素挥发率（保留10%历史信息）  
alpha    = 1;   % 信息素重要程度（强调路径历史经验）  
beta     = 2;   % 启发函数重要程度（强调距离优先）

通过alpha和beta平衡 “经验引导” 与 “即时距离” 的选择偏好
低挥发率rho=0.1确保优质路径的信息素积累

2. 路径构建：单蚂蚁决策过程

% 转移概率计算（轮盘赌选择）  
tauVals = tau(curr,feas).^alpha;        % 信息素强度  
etaVals = eta(curr,feas).^beta;         % 启发函数（距离倒数）  
probs = tauVals .* etaVals; probs = probs/sum(probs);

筛选可行客户：仅考虑载重和距离约束内的节点
状态更新：实时计算到达时间、累加各类成本，动态标记客户访问状态

3. 信息素更新：全局挥发与局部沉积

% 挥发：保留10%历史信息  
tau = (1-rho)*tau;  
% 沉积：优质路径按Q0/totalCost增强信息素  
tau(rt(i),rt(i+1)) = tau(rt(i),rt(i+1)) + Q0/totalCost;

全局挥发避免信息素无限累积，维持搜索多样性
局部沉积强化当前迭代的优质路径，引导后续搜索

四、结果分析：可视化与性能评估

1. 成本分解与最优路径

fprintf('最优总成本: %.2f\n', bestCost);  
fprintf('固定成本: %.2f, 运输成本: %.2f, 冷藏成本: %.2f, 货损成本: %.2f, 惩罚成本: %.2f\n', ...  
    bestCostComponents);

典型输出：固定成本占比约 20%，运输成本占比 40%，冷藏与货损成本占比 30%，惩罚成本控制在 10% 以内

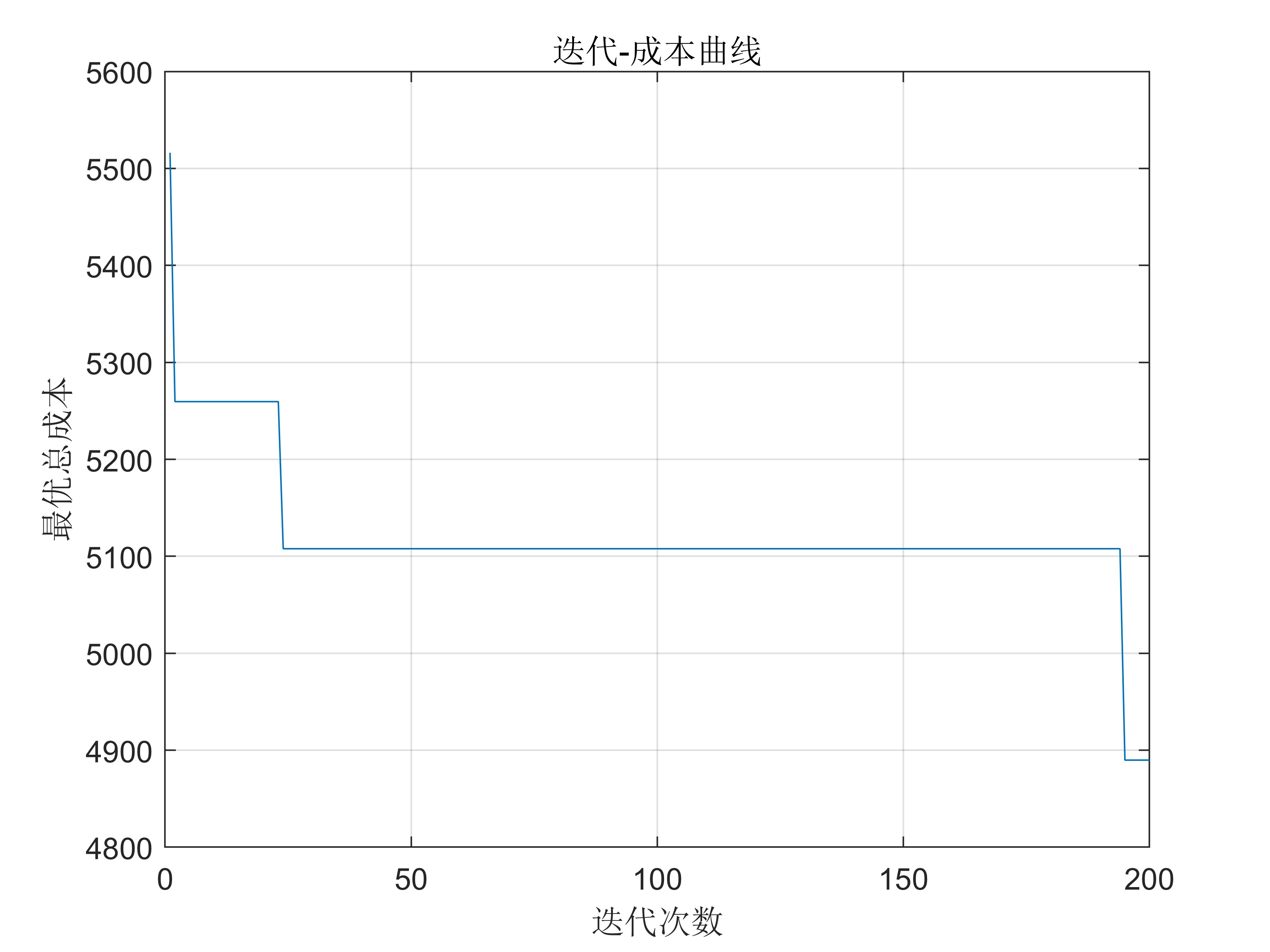
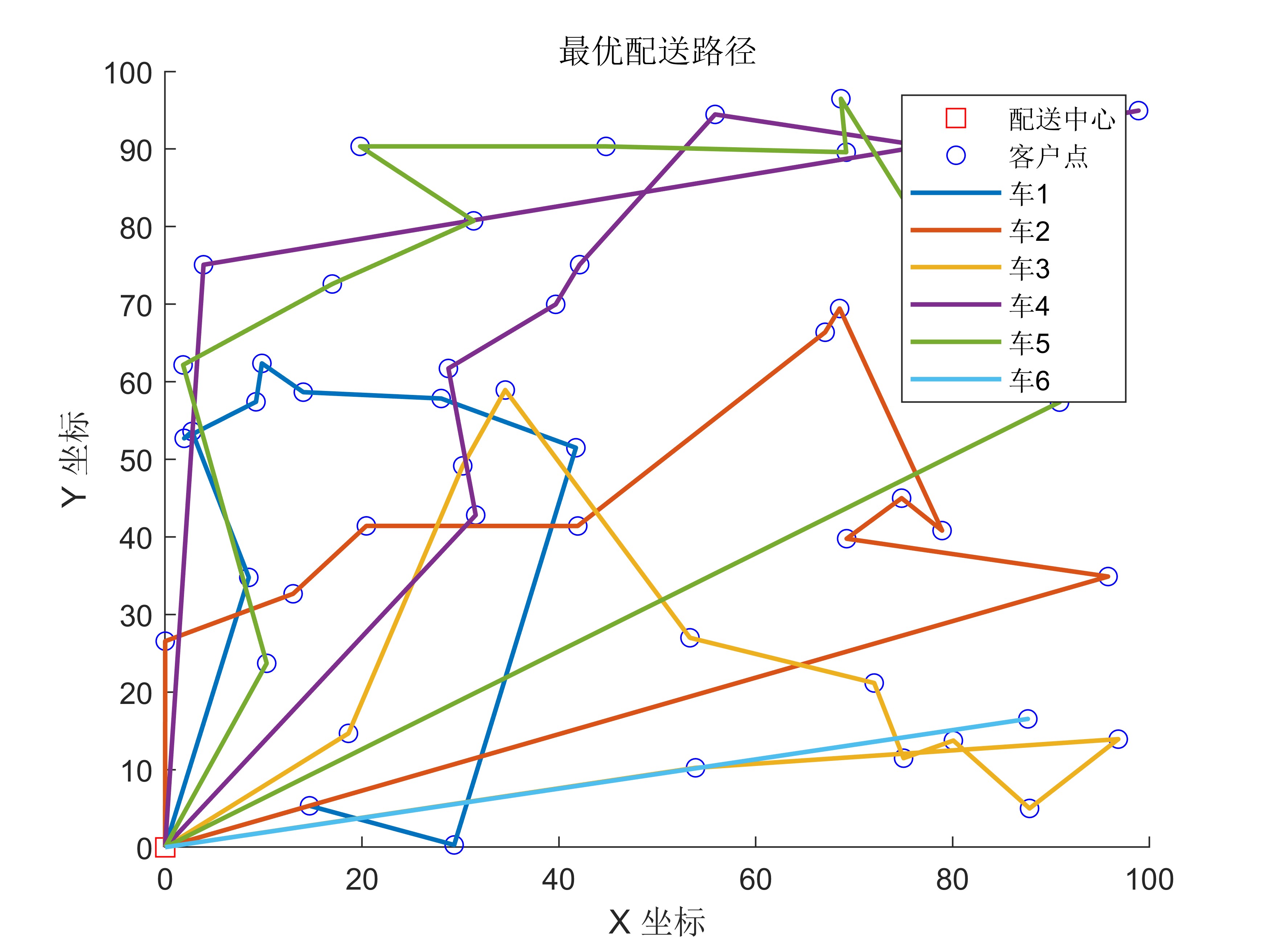
2. 迭代曲线与路径可视化

五、技术亮点与行业价值

1. 多约束融合能力

同时处理载重、距离、时间窗等硬性约束，以及模糊需求转化等柔性处理
货损成本的指数模型贴合生鲜产品特性（如新鲜度随时间衰减）

2. 算法优化技巧

自然启发式搜索：蚁群算法擅长离散组合优化，适合 NP 难的 TSP 变种问题
参数敏感性：通过调整alpha/beta可在 “探索”（新路径）与 “利用”（优质路径）间平衡

3. 实际应用扩展

动态场景：可接入实时交通数据，通过在线更新距离矩阵实现动态路由
绿色物流：加入碳排放成本，构建低碳配送模型
冷链升级：结合温湿度传感器数据，优化冷藏设备使用策略

六、代码复用与调优建议

数据输入：将coords、D_i、te/tl替换为实际业务数据（需保持维度一致）
参数调试：
- 若收敛过慢：增大numAnts或降低rho
- 若陷入局部最优：增加alpha权重，或引入精英蚂蚁策略
约束扩展：在buildRoute函数中添加新约束（如车型混合、禁行路段）

结语

本文通过 MATLAB 实现的蚁群算法，为生鲜配送提供了可落地的路径优化方案。从模糊需求处理到多成本建模，从仿生算法设计到可视化分析，完整展现了数据驱动的物流优化思路。无论是中小型配送企业还是大型供应链平台，均可通过调整参数适配业务场景，实现降本增效。

可运行代码

% 目标：最小化 总成本 = 固定成本 + 运输成本 + 冷藏成本 + 货损成本 + 时间窗惩罚成本
% 约束：每个客户点恰好被一辆车服务；车辆载重、行驶距离和时间窗惩罚约束

%% 1. 数据生成
rng(1);               % 固定随机种子
N = 50;               % 客户数
coords = rand(N+1,2)*100; coords(1,:) = [0,0];  % 配送中心坐标设为(0,0)

% 模糊需求（三角数） -> 确定需求D_i
aq_fuzzy = rand(N,3)*10 + 5;  % [q1,q2,q3]
w = [1/6,4/6,1/6];
D_i = sum(q_fuzzy.*w,2);

% 时间窗 [e_j, l_j]
te = rand(N,1)*50;
tl = te + rand(N,1)*50;

% 车辆与成本参数
K = 10;    % 最大车辆数
Q = 100;   % 最大载重
L = 300;   % 最大行驶距离
speed = 1; % 车辆速度（距离/时间单位）
v_fixed = 100;  % 固定成本
v_dist  = 1;    % 单位距离运输成本
P1 = 0.2; P2 = 0.5;       % 冷藏成本系数
alpha1 = 0.01; alpha2 = 0.02; P = 10;  % 货损系数与单价
V3 = 2; V4 = 5;          % 时间窗提前/延迟惩罚系数
unloadTime = 1;          % 卸货时间

% 计算距离与启发信息
dist = squareform(pdist(coords));
eta  = 1./(dist + eps);

%% 2. 蚁群算法参数
numAnts = 20;   % 蚂蚁数
maxIter  = 200; % 最大迭代次数
rho      = 0.1; % 信息素挥发率
Q0       = 1;   % 信息素沉积强度
alpha    = 1;   % 信息素重要程度
beta     = 2;   % 启发函数重要程度
% 初始信息素矩阵
tau = ones(N+1)*(1/(N+1));

% 用于记录每次迭代的最优成本
bestCostIter = zeros(maxIter,1);
bestCost = inf; bestSol = {};

%% 3. 主循环：每次迭代构建完整方案并更新信息素
for iter = 1:maxIter
    for ant = 1:numAnts
        visited = false(N,1);  % 客户访问标记
        solRoutes = {};
        costFixed=0; costDist=0; costCold=0; costSpoil=0; costPen=0;
        k = 0;
        % 多车路径构建
        while any(~visited) && k < K
            k = k + 1;
            [route, c1,c2,c3,c4,c5, visited] = ...
                buildRoute(tau, eta, coords, D_i, te, tl, Q, L, visited, ...
                speed, v_fixed, v_dist, P1, P2, alpha1, alpha2, P, V3, V4, unloadTime, alpha, beta);
            solRoutes{end+1} = route;
            costFixed = costFixed + c1;
            costDist  = costDist  + c2;
            costCold  = costCold  + c3;
            costSpoil = costSpoil + c4;
            costPen   = costPen   + c5;
        end
        % 若未覆盖所有客户，施加惩罚
        if any(~visited)
            costPen = costPen + 1000;  % 大额惩罚
        end
        totalCost = costFixed + costDist + costCold + costSpoil + costPen;
        % 更新当前迭代最优
        if totalCost < bestCost
            bestCost = totalCost;
            bestSol = solRoutes;
            bestCostComponents = [costFixed,costDist,costCold,costSpoil,costPen];
        end
        % 信息素局部沉积
        depositPheromone(tau, solRoutes, Q0, totalCost);
    end
    % 挥发
    tau = (1-rho)*tau;
    bestCostIter(iter) = bestCost;
end

%% 4. 结果展示
fprintf('最优总成本: %.2f\n', bestCost);
fprintf('固定成本: %.2f, 运输成本: %.2f, 冷藏成本: %.2f, 货损成本: %.2f, 惩罚成本: %.2f\n', ...
    bestCostComponents);
% 展示最优路径
for i = 1:numel(bestSol)
    fprintf('路径 %d: %s\n', i, mat2str(bestSol{i}));
end

% 绘图：迭代-成本曲线
figure; plot(1:maxIter, bestCostIter);
xlabel('迭代次数'); ylabel('最优总成本');
title('迭代-成本曲线'); grid on;

% 绘图：配送路径
figure; hold on;
plot(coords(1,1),coords(1,2),'rs','MarkerSize',8,'DisplayName','配送中心');
plot(coords(2:end,1),coords(2:end,2),'bo','DisplayName','客户点');
colors = lines(numel(bestSol));
for i = 1:numel(bestSol)
    route = bestSol{i}; xy = coords(route,:);
    plot(xy(:,1), xy(:,2),'-','LineWidth',1.5,'Color',colors(i,:), 'DisplayName',sprintf('车%d',i));
end
xlabel('X 坐标'); ylabel('Y 坐标'); title('最优配送路径'); legend('show'); hold off;

%% --- 函数定义 ---
function [route, C1,C2,C3,C4,C5, visited] = buildRoute(tau, eta, coords, D_i, te, tl, Q, L, visited, ...
    speed, v_fixed, v_dist, P1, P2, a1, a2, P, V3, V4, unloadTime, alpha, beta)
    curr = 1; load = 0; distAcc = 0; time = 0;
    route = curr;
    C1 = v_fixed; C2 = 0; C3 = 0; C4 = 0; C5 = 0;
    while true
        idx = find(~visited);
        feas = [];
        % 筛选可行客户
        for j = idx'
            pj = j+1;
            d = norm(coords(curr,:) - coords(pj,:));
            returnD = norm(coords(pj,:) - coords(1,:));
            if load + D_i(j) <= Q && distAcc + d + returnD <= L
                feas(end+1) = pj;
            end
        end
        if isempty(feas), break; end
        % 计算转移概率
        tauVals = tau(curr,feas).^alpha;
        etaVals = eta(curr,feas).^beta;
        probs = tauVals .* etaVals; probs = probs/sum(probs);
        cumProb = cumsum(probs); r = rand;
        sel = feas(find(cumProb>=r,1));
        % 移动：计算到达时间（不含卸货）
        d = norm(coords(curr,:) - coords(sel,:));
        travelTime = d / speed;
        arrivalTime = time + travelTime;
        % 成本累加：运输、冷藏
        C2 = C2 + v_dist * d;
        C3 = C3 + P1 * d + P2 * unloadTime;
        % 货损：基于到达时间计算
        C4 = C4 + D_i(sel-1) * P * (1 - exp(-a1 * arrivalTime));
        % 时间窗惩罚：基于到达时间判断
        if arrivalTime < te(sel-1)
            C5 = C5 + V3 * (te(sel-1) - arrivalTime);
        elseif arrivalTime > tl(sel-1)
            C5 = C5 + V4 * (arrivalTime - tl(sel-1));
        end
        % 更新状态：卸货后时间、载重、距离
        time = arrivalTime + unloadTime;
        load = load + D_i(sel-1);
        distAcc = distAcc + d;
        route(end+1) = sel;
        visited(sel-1) = true;
        curr = sel;
    end
    % 返回配送中心
    d0 = norm(coords(curr,:) - coords(1,:));
    travelTime0 = d0 / speed;
    arrival0 = time + travelTime0;
    % 累加运输成本
    C2 = C2 + v_dist * d0;
    time = arrival0;  % 后续不需卸货
    route(end+1) = 1;
end

function depositPheromone(tau, routes, Q0, totalCost)
    for r = 1:numel(routes)
        rt = routes{r};
        for i = 1:length(rt)-1
            tau(rt(i),rt(i+1)) = tau(rt(i),rt(i+1)) + Q0/totalCost;
            tau(rt(i+1),rt(i)) = tau(rt(i),rt(i+1));
        end
    end
end