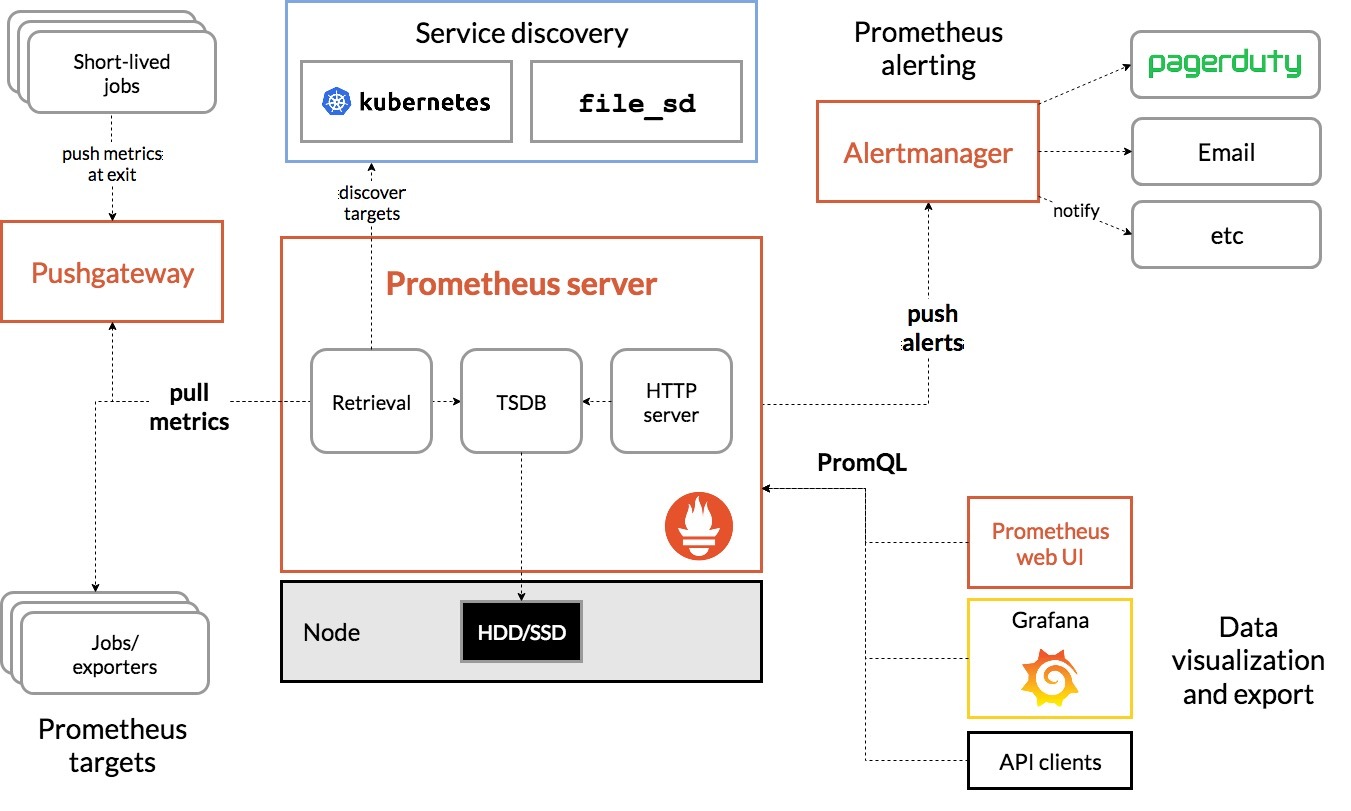
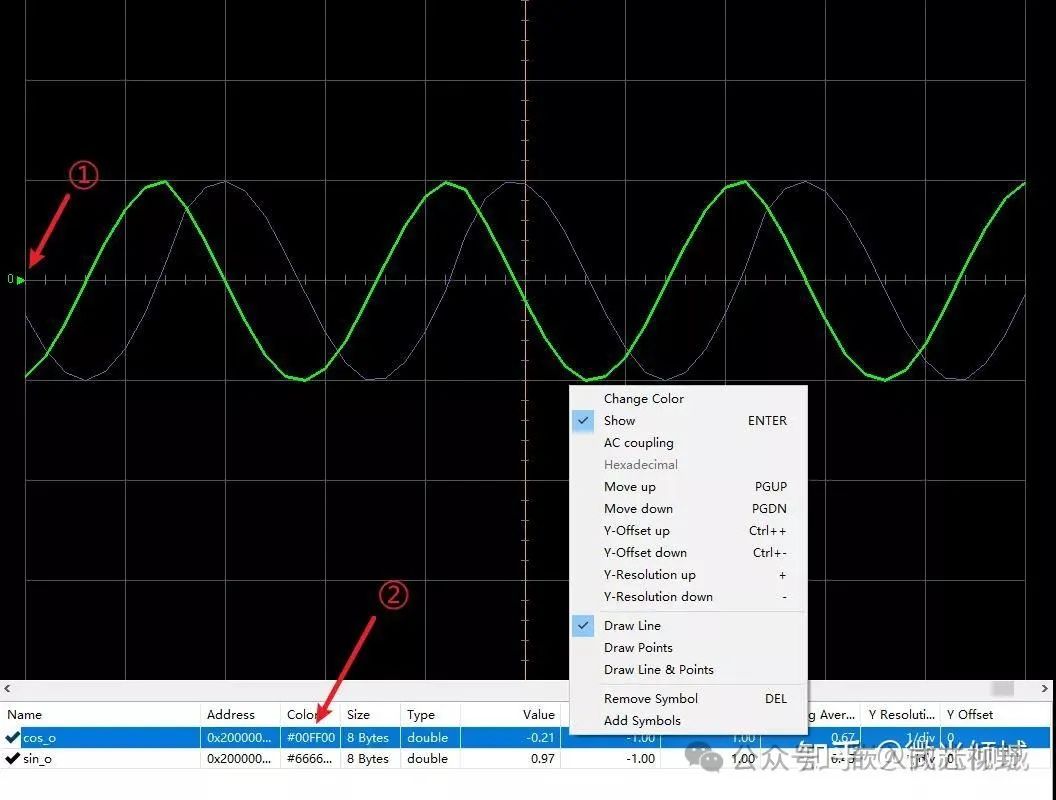
1.特征和多项式回归
如房价预测问题,

ℎθ (x) = θ0 + θ1 × frontage + θ2 × deptℎ
x1 = frontage(临街宽度),x2 = deptℎ(纵向深度),x = frontage ∗ deptℎ = area (面积),则:
h
θ
(
x
)
=
θ
0
+
θ
1
x
h_\theta(x) = \theta_0 + \theta_1x
hθ(x)=θ0+θ1x

线性回归并不适用于所有数据,有时我们需要曲线来适应我们的数据,比如一个二次方模型:
h
θ
(
x
)
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
2
ℎ_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2^2
hθ(x)=θ0+θ1x1+θ2x22
或者三次方模型:
h
θ
(
x
)
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
2
+
θ
3
x
3
3
ℎ_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2^2 + \theta_3x_3^3
hθ(x)=θ0+θ1x1+θ2x22+θ3x33
通常我们需要先观察数据然后再决定准备尝试怎样的模型。 另外,我们可以令:
x2 =
x
2
2
x_2^2
x22, x3 =
x
3
3
x_3^3
x33,从而将模型转化为线性回归模型。 根据函数图形特性,我们还可以使:
h
θ
(
x
)
=
θ
0
+
θ
1
⋅
size
+
θ
2
⋅
size
2
h_\theta(x) = \theta_0 + \theta_1 \cdot \text{size} + \theta_2 \cdot \text{size}^2
hθ(x)=θ0+θ1⋅size+θ2⋅size2或者:
h
θ
(
x
)
=
θ
0
+
θ
1
⋅
size
+
θ
2
⋅
size
ℎθ (x) = θ_0 + θ_1 \cdot \text{size} + θ_2 \cdot \sqrt{\text{size}}
hθ(x)=θ0+θ1⋅size+θ2⋅size
注:如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。