目录
1 回溯法
1.1 N皇后问题
1.1.1 非递归求解N皇后问题
1.1.2 递归求解N皇后问题
1.2 真题
2 分治法
2.1 真题
3 动态规划法
3.1 0-1背包问题
3.2 真题

1 回溯法

1.1 N皇后问题
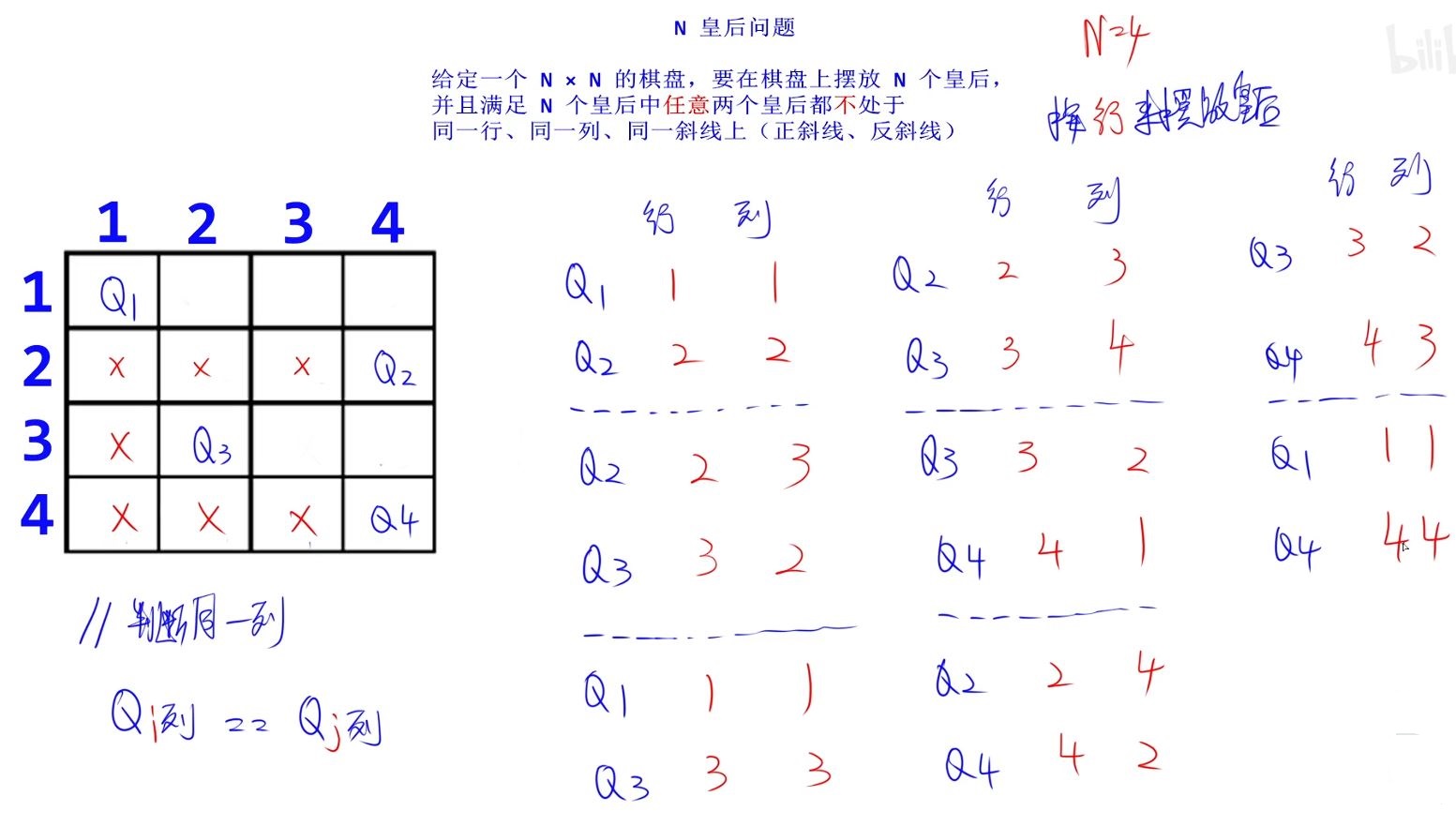
上图Q4与Q2在同一列且与Q1在同一斜线,先回溯到上一个皇后改变Q3皇后的位置,若不行,再向上回溯,直到回溯到第一个皇后位置可行,再向下回溯,直到每个皇后位置都可行。

在软考中,最终表示如下


1.1.1 非递归求解N皇后问题

#include <math.h>
#include <stdio.h>
#define N 4
// #define N 10
int q[N + 1]; // 存储皇后的列号
int check(int j) { // 检查第 j 个皇后的位置是否合法
int i;
for (i = 1; i < j; i ++ ) {
if (q[i] == q[j] || abs(i - j) == abs(q[i] - q[j])) { // 判断是否在同一列和同一斜线上
return 0;
}
}
return 1;
}
void queen() { // 求解 N 皇后 方案
int i;
for (i = 1; i <= N; i ++ ) {
q[i] = 0;
}
int answer = 0; // 方案数
int j = 1; // 表示正在摆放第 j 个皇后
while (j >= 1) {
q[j] = q[j] + 1; // 让第 j 个皇后向后一列摆放
while (q[j] <= N && !check(j)) { // 判断第 j 个皇后的位置是否合法
q[j] = q[j] + 1; // 不合法就往后一个位置摆放
}
if (q[j] <= N) { // 表示第 j 个皇后的找到一个合法的摆放位置
if (j == N) { // 找到了 N 皇后的一组解
answer = answer + 1;
printf("方案%d:", answer);
for (i = 1; i <= N; i ++ ) {
printf("%d ", q[i]);
}
printf("\n");
} else {
j = j + 1; // 继续摆放下一个皇后
}
} else { // 表示第 j 个皇后找不到一个合法的摆放位置
q[j] = 0; // 还原第 j 个皇后的位置
j = j - 1; // 回溯
}
}
}
int main() {
queen();
return 0;
}
1.1.2 递归求解N皇后问题

#include <math.h>
#include <stdio.h>
#define N 4
// #define N 10
int answer = 0;
int q[N + 1]; // 存储皇后的列号
int check(int j) { // 检查第 j 个皇后的位置是否合法
int i;
for (i = 1; i < j; i ++ ) {
if (q[i] == q[j] || abs(i - j) == abs(q[i] - q[j])) { // 判断是否在同一列和同一斜线上
return 0;
}
}
return 1;
}
void queen(int j) {
int i;
for (i = 1; i <= N; i ++ ) {
q[j] = i;
if (check(j)) { // 当摆放的皇后位置为合法时
if (j == N) { // 找到了 N 皇后的一组解
answer = answer + 1;
printf("方案%d:", answer);
for (i = 1; i <= N; i ++ ) {
printf("%d ", q[i]);
}
printf("\n");
} else {
queen(j + 1); // 递归摆放下一个皇后的位置
}
}
}
}
int main() {
queen(1);
return 0;
}
1.2 真题
1.2015年上半年





2.2019年上半年





2 分治法






#include <stdio.h>
#include <sched.h>
void Merge(int A[], int p, int q, int r) {
int i, j, k;
int L[50], R[50];
int n1 = q - p + 1, n2 = r - q;
for (i = 0; i < n1; i ++ ) {
L[i] = A[p + i];
}
for (j = 0; j < n2; j ++ ) {
R[j] = A[q + j + 1];
}
L[n1] = INT_MAX;
R[n2] = INT_MAX;
i = 0;
j = 0;
for (k = p; k < r + 1; k ++ ) {
if (L[i] < R[j]) {
A[k] = L[i];
i ++ ;
} else {
A[k] = R[j];
j ++ ;
}
}
}
void MergeSort(int A[], int p, int r) {
int q;
if (p < r) {
q = (p + r) / 2;
MergeSort(A, p, q);
MergeSort(A, q + 1, r);
Merge(A, p, q, r);
}
}
int main() {
int A[] = {4, 1, 3, 6, 8, 5, 2, 9};
MergeSort(A, 0, 7);
int i;
for (i = 0; i < 8; i ++ ) {
printf("%d ", A[i]);
}
return 0;
}

2.1 真题
1.2014年上半年









2.2017年上半年








3.2020年下半年






3 动态规划法




3.1 0-1背包问题


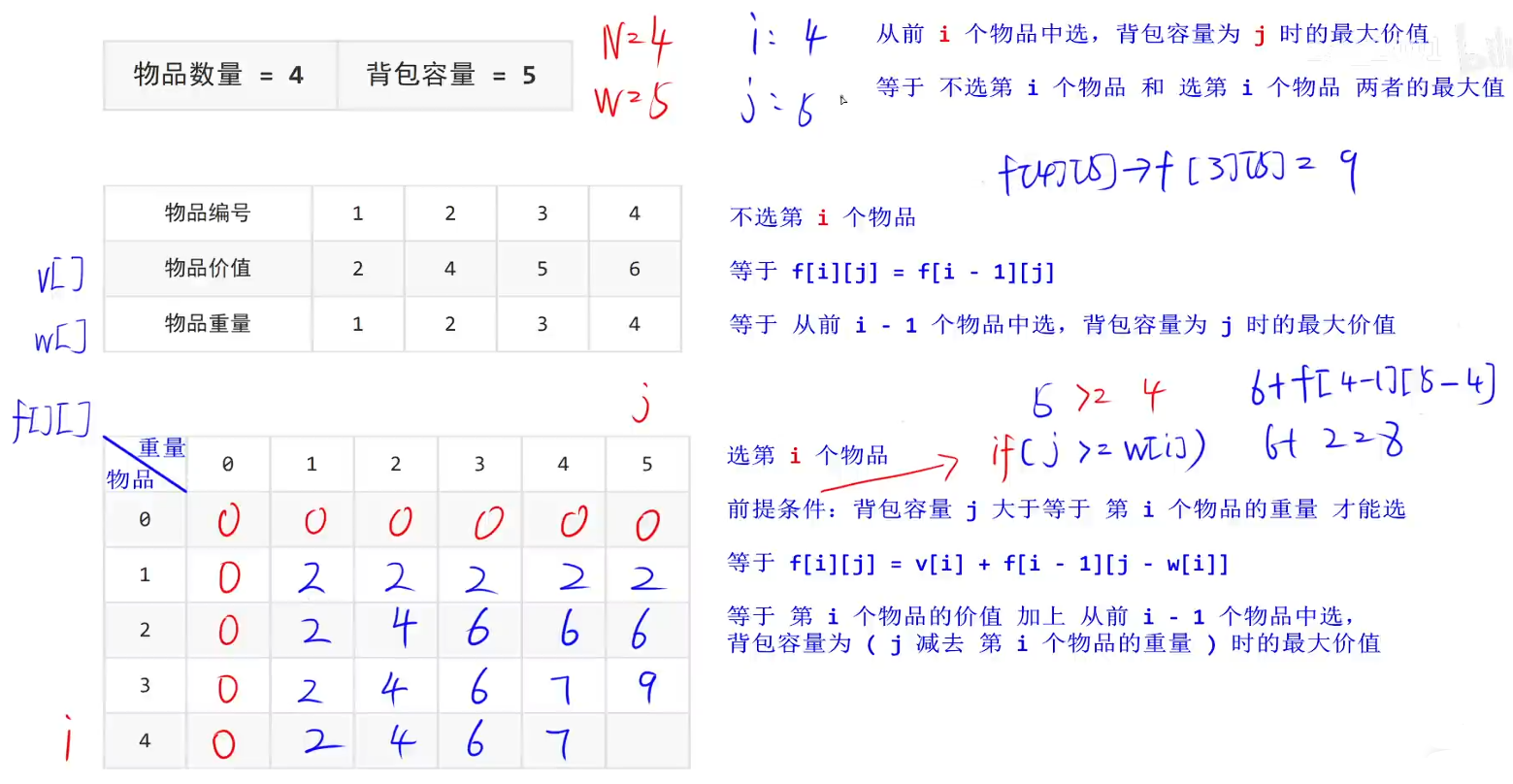

#include <stdio.h>
#define N 4 // 物品数量
#define W 5 // 背包容量
int max(int a, int b) {
return a > b ? a : b;
}
int main() {
int v[] = {0, 2, 4, 5, 6}; // 物品价值数组
int w[] = {0, 1, 2, 3, 4}; // 物品重量数组
int f[N + 1][W + 1] = {}; // 子问题解数组
int i, j;
for (i = 1; i <= N; i ++ ) {
for (j = 1; j <= W; j ++ ) {
f[i][j] = f[i - 1][j]; // 默认不选第 i 个物品
if (j >= w[i]) { // 选第 i 个物品的前提条件
// 等于 不选第 i 个物品 和 选第 i 个物品 两者的较大值
f[i][j] = max(f[i][j], f[i - 1][j - w[i]] + v[i]);
}
// 上方是写法 1
/* ============================================================ */
// 下方是写法 2
/*
if (j >= w[i]) { // 选第 i 个物品的前提条件
// 等于 不选第 i 个物品 和 选第 i 个物品 两者的较大值
f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]);
} else { // 不选第 i 个物品
f[i][j] = f[i - 1][j]; // 等于 从前 i - 1 个物品中选,背包容量为 j 时的最大价值
}
*/
}
}
printf("%d\n", f[N][W]);
for (i = 0; i <= N; i ++ ) {
for (j = 0; j <= W; j ++ ) {
printf("%d ", f[i][j]);
}
printf("\n");
}
return 0;
}


3.2 真题
1.2019年下半年







2.2021年下半年