目录
1.单值二叉树
2.相同的树
3.对称二叉树
4.二叉树的前序遍历
5.另一颗树的子树
1.单值二叉树

思路1:
判断根节点、左节点与右节点的值是否相等,因为正向判断(即判断三值相等返回true)比较麻烦(不能根节点满足条件直接返回true,还需进行左右子树的判断),因此可以通过正难则反的思想,判断哪些情况不是单值二叉树
最后的返回值应该是整棵树根节点,左右子树进行相与操作(即&&)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isUnivalTree(struct TreeNode* root) {
if(root == NULL) return true;
if(root->left && root->left->val!=root->val) return false;
if(root->right && root->right->val!=root->val) return false;
return isUnivalTree(root->left)&&isUnivalTree(root->right);
}思路2:
把根节点的值作为判断标准,遍历整棵树进行判断
代码将会使用前序遍历的方法进行判断
鉴于使用bool类型的函数来完成前序遍历比较难,此处可以使用一个判断标志,在传参时把判断标志的地址一起传过去
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
void PrevOrder(struct TreeNode* root ,int val, int* pa)
{
if (root == NULL)
{
return;
}
if(root->val!=val)
{
*pa=0;
}
PrevOrder(root->left,val,pa);
PrevOrder(root->right,val,pa);
return;
}
bool isUnivalTree(struct TreeNode* root) {
int a=1;
PrevOrder(root,root->val,&a);
if(a){
return true;
}else{
return false;
}
}2.相同的树

/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
//两者皆空
if(p==NULL&&q==NULL) return true;
//其中一个为空,一个不为空
if(p==NULL||q==NULL) return false;
//两者都不为空
if(p->val != q->val) return false;
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}代码重点讲解:
以左右子树为判断的依据,因此最后返回的是isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);此时可能会担心一个问题,根节点会不会判断?肯定会判断的,如果根节点在前面一条语句 if(p->val != q->val) return false; 没有返回false说明是true,最后通过递归调用语句返回的也还是原来结果
分为以下3种情况:
1.两者皆空
2.只有一个为空:p==NULL||q==NULL 通过或运算,两者皆空在前面已经判断掉了,因此此处可以这么写
3.两者都不为空:如果根节点相同了,但左子树或右子树不同,最后还是会返回true;因此继续使用正难则反的思想,判断不相同的情况;这样左右子树即使都为true,根节点不对依旧会返回false
3.对称二叉树

对称二叉树的根节点怎么样不会影响最终结果,因此就是去判断整棵树根节点的左右子树(假设看作a、b子树)是否对称就行
判断对称的办法:和判断相同类似,唯一的区别在于递归调用时,左子树和右子树进行比较,右子树和左子树进行比较(这边的左右子树指的是a、b子树的根节点后面所连接的左右子树)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isSymmetricTree(struct TreeNode* p, struct TreeNode* q) {
//两者皆空
if(p==NULL&&q==NULL) return true;
//其中一个为空,一个不为空
if(p==NULL||q==NULL) return false;
//两者都不为空
if(p->val != q->val) return false;
return isSymmetricTree(p->left,q->right)&&isSymmetricTree(p->right,q->left);
}
bool isSymmetric(struct TreeNode* root) {
return isSymmetricTree(root->left,root->right);
}4.二叉树的前序遍历

/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int TreeSize(struct TreeNode* root)
{
return root == NULL ? 0 : TreeSize(root->left)+TreeSize(root->right)+1;
}
void prevOrder(struct TreeNode* root,int* a,int* pi)
{
if(root==NULL) return;
a[(*pi)++] = root->val;
prevOrder(root->left,a,pi);
prevOrder(root->right,a,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
int size;
*returnSize = size = TreeSize(root);
int* a = (int*)malloc(sizeof(int)*size);
int i=0;
prevOrder(root,a,&i);
return a;
}代码重点讲解:
int* returnSize :leetcode特色,代表的是返回的数组大小;因为数组创建这一步是在函数中由做题者完成,因此最后返回时,也需要有个数组大小;此处传来的是指针,因此直接解引用后赋值即可(leetcode的main函数逻辑如下)
int main()
{
//……
int n = 0;
preorderTraversal(root,n);
//……
}代码重点讲解:
prevOrder(root,a,i):为什么最后的 i 要传其地址?
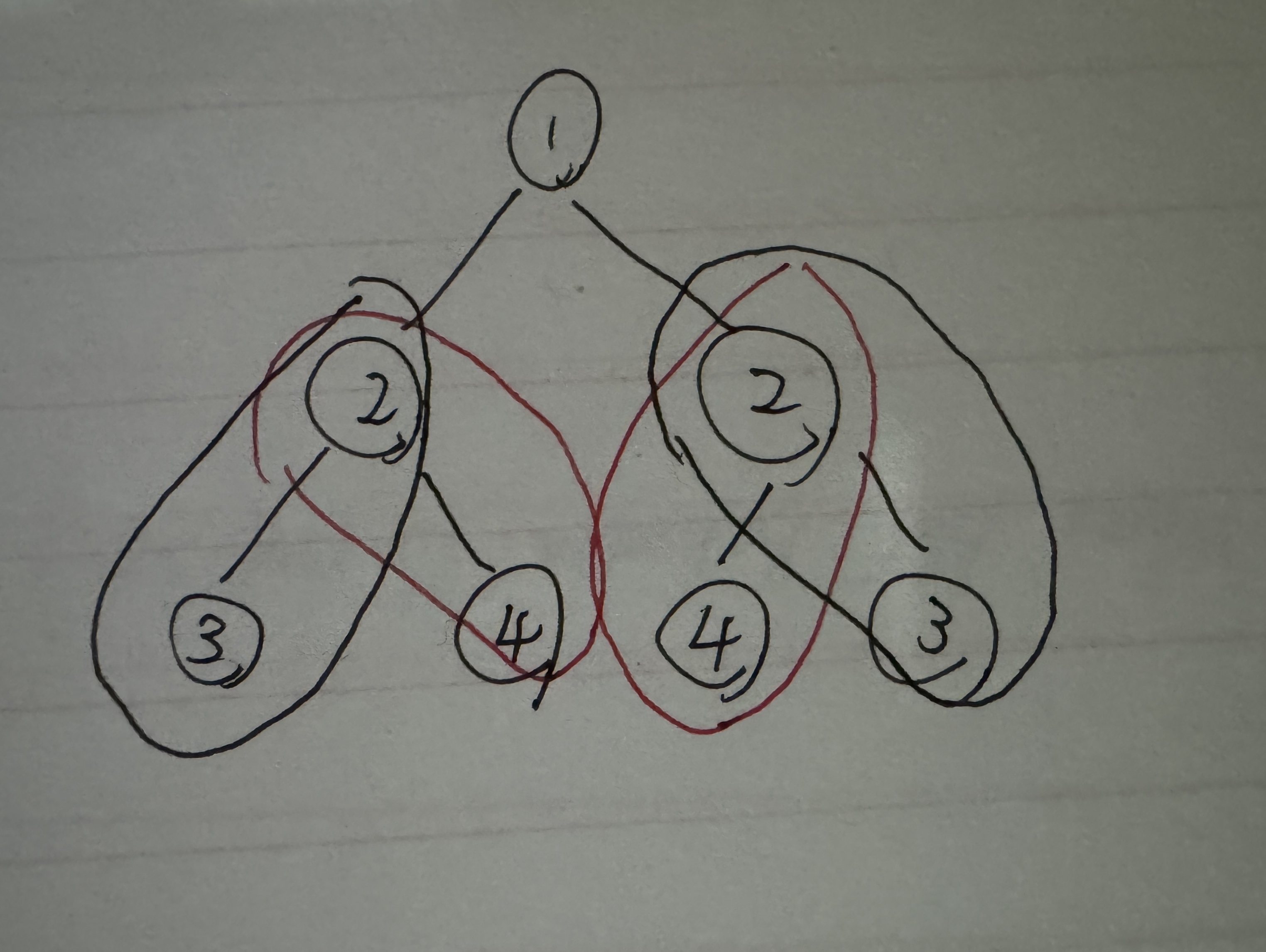
i 代表的是数组下标,若不传其地址,那么形参的改变不会致使实参的改变;此时,在递的过程中,i 依然会不断地变大;但在归的过程中,i 会回到原来那个函数的大小,此时 i 下标又被传给了prevOrder(root->right),这样 i 坐标就被新值覆盖掉了。综上所述,我们需要传递i的地址,让每一次i的变化能影响到每一层递归调用的函数。
下图为图像解释

5.另一颗树的子树

/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
//两者皆空
if(p==NULL&&q==NULL) return true;
//其中一个为空,一个不为空
if(p==NULL||q==NULL) return false;
//两者都不为空,如果根节点相同了,但左子树或右子树不同,最后还是会返回true;因此继续使用正难则反的思想,判断不相同的情况;这样左右子树即使都为true,根节点不对依旧会返回false
if(p->val != q->val) return false;
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
if(root==NULL) return false;
if(root->val == subRoot->val && isSameTree(root,subRoot)) return true;
return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}代码重点讲解:
只要左右子树中,有一个是满足条件的,就可以返回true,因此最终返回isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot)
当左右子树的根节点相等时,可以通过判断以改根节点为子树的与subRoot是否相等,来判断在整棵树中是否存在subRoot一样的树
当左右子树为空时,因为subRoot的结点个数范围为[1,1000],因此直接返回false即可