字符串检索算法：KMP和Trie树

news2025/7/13 21:06:42

目录

1.引言

2.KMP算法

3.Trie树

3.1.简介

3.2.Trie树的应用场景

3.3.复杂度分析

3.4.Trie 树的优缺点

3.5.示例

1.引言

        字符串匹配，给定一个主串 S 和一个模式串 P，判断 P 是否是 S 的子串，即找到 P 在 S 中第一次出现的位置。暴力匹配的思路是：从主串 S 的每个位置开始，逐个字符与模式串 P 比较。若匹配失败，主串指针回退到起始位置的下一个位置，重新开始匹配。 时间复杂度：最坏情况下为 O(n×m)（n 为主串长度，m 为模式串长度）。缺陷：当模式串存在重复前缀或后缀时，重复比较了很多已知信息，效率低下。于是就引出了KMP算法。

2.KMP算法

        要理解KMP算法，首先要搞清楚真前缀与真后缀。在一个字符串中，真前缀是指除了最后一个字符外，一个字符串的头部连续的若干字符；真后缀是指除了第一个字符外，一个字符串的尾部连续的若干字符。举个例子：

        字符串："ABCDABD"

        真前缀："A"、"AB"、"ABC"、"ABCD"、"ABCDA"、"ABCDAB"

        真后缀："BCDABD"、"CDABD"、"DABD"、"ABD"、"BD"、"D"

递推计算next数组

        next 数组的求解基于“真前缀”和“真后缀”，即next[i]等于P[0]...P[i - 1]最长的相同真前后缀的长度（首先设置next[0]=-1,边界条件）。我们以表格为例：

i01234567
模式串ABCDABD'\0'
next[ i ]-10000120
  1. i = 0，对于模式串的首字符，我们统一为next[0] = -1；
  2. i = 1，前面的字符串为A，其最长相同真前后缀长度为 0，即next[1] = 0；
  3. i = 2，前面的字符串为AB，其最长相同真前后缀长度为 0，即next[2] = 0；
  4. i = 3，前面的字符串为ABC，其最长相同真前后缀长度为 0，即next[3] = 0；
  5. i = 4，前面的字符串为ABCD，其最长相同真前后缀长度为 0，即next[4] = 0；
  6. i = 5，前面的字符串为ABCDA，其最长相同真前后缀为A，即next[5] = 1；
  7. i = 6，前面的字符串为ABCDAB，其最长相同真前后缀为AB，即next[6] = 2；
  8. i = 7，前面的字符串为ABCDABD，其最长相同真前后缀长度为 0，即next[7] = 0。

        那么，为什么根据最长相同真前后缀的长度就可以实现在不匹配情况下的跳转呢？举个代表性的例子：假如i = 6时不匹配，此时我们是知道其位置前的字符串为ABCDAB，仔细观察这个字符串，首尾都有一个AB，既然在i = 6处的 D 不匹配，我们为何不直接把i = 2处的 C 拿过来继续比较呢，因为都有一个AB啊，而这个AB就是ABCDAB的最长相同真前后缀，其长度 2 正好是跳转的下标位置。

        思路如此简单，接下来就是代码实现了，如下：

// 生成Next数组, 示例：“GTGTGCF”
std::vector<int> buildNext(const std::string& pattern) {
    std::vector<int> next(pattern.size(), 0);
    int j = 0;
    for (int i = 2; i < pattern.length(); i++) {
        while (j != 0 && pattern[j] != pattern[i - 1]) {
            //从next[i+1]的求解回溯到 next[j]
            j = next[j];
        }
        if (pattern[j] == pattern[i - 1]) {
            j++;
        }
        next[i] = j;
    }
    return next;
}
int kmpSearch(const std::string& text, const std::string& pattern) {
    //预处理，生成next数组
    std::vector<int> next(std::move(buildNext(pattern)));
    int j = 0;
    //主循环，遍历主串字符
    for (int i = 0; i < text.length(); i++) {
        while (j > 0 && text[i] != pattern[j]) {
            //遇到坏字符时，查询next数组并改变模式串的起点
            j = next[j];
        }
        if (text[i] == pattern[j]) {
            j++;
        }
        if (j == pattern.length()) {
            //匹配成功，返回下标
            return i - pattern.length() + 1;
        }
    }
    return  -1;
}

复杂度分析：

  • 时间复杂度：
    • 构建 next 数组：O(m)（每个字符最多被访问两次）。
    • 匹配过程：O(n)（主串指针 i 仅递增，不回退）。
    • 总复杂度：O(n+m)，优于暴力匹配的 O(n×m)。
  • 空间复杂度：O(m)（存储 next 数组）。

3.Trie树

3.1.简介

        Trie树，即前缀树，又称单词查找树，字典树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。

  Trie树的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。 它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。

它有3个基本性质：

  1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
  2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
  3. 每个节点的所有子节点包含的字符都不相同。

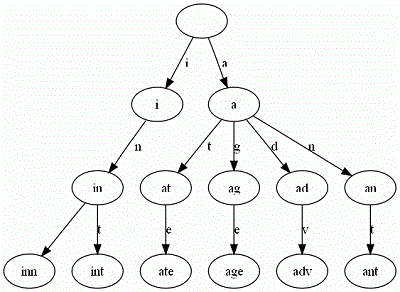
举一个例子。给出一组单词，inn, int, at, age, adv, ant, 我们可以得到下面的Trie：

3.2.Trie树的应用场景

字符串检索，词频统计，搜索引擎的热门查询

        trie树在大数据查找和检索方面具有独特的优势，不过就是要求内存比较高，不过在没有内存限制的情况不适为一种好的方式，如：(节选自此文：海量数据处理面试题集锦与Bit-map详解)

a）有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词。

b） 1000万字符串，其中有些是重复的，需要把重复的全部去掉，保留没有重复的字符串。请怎么设计和实现？

c）寻找热门查询：搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来，每个查询串的长度为1-255字节。假设目前有一千万个记录，这些查询串的重复读比较高，虽然总数是1千万，但是如果去除重复和，不超过3百万个。一个查询串的重复度越高，说明查询它的用户越多，也就越热门。请你统计最热门的10个查询串，要求使用的内存不能超过1G。

d）一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词，请给出思想，给出时间复杂度分析

e) 给出一个词典，其中的单词为不良单词。单词均为小写字母。再给出一段文本，文本的每一行也由小写字母构成。判断文本中是否含有任何不良单词。例如，若rob是不良单词，那么文本problem含有不良单词。

(1) 请描述你解决这个问题的思路；
(2) 请给出主要的处理流程，算法，以及算法的复杂度。

字符串最长公共前缀

        Trie树利用多个字符串的公共前缀来节省存储空间，反之，当我们把大量字符串存储到一棵trie树上时，我们可以快速得到某些字符串的公共前缀。举例：

      给出N 个小写英文字母串，以及Q 个询问，即询问某两个串的最长公共前缀的长度是多少.  解决方案：

        首先对所有的串建立其对应的字母树。此时发现，对于两个串的最长公共前缀的长度即它们所在结点的公共祖先个数，于是，问题就转化为了离线  （Offline）的最近公共祖先（Least Common Ancestor，简称LCA）问题。

       而最近公共祖先问题同样是一个经典问题，可以用下面几种方法：

        1. 利用并查集（Disjoint Set），可以采用采用经典的Tarjan 算法；

        2. 求出字母树的欧拉序列（Euler Sequence ）后，就可以转为经典的最小值查询（Range Minimum Query，简称RMQ）问题了；

3.3.复杂度分析

  • 插入操作：时间复杂度为 O (m)，这里的 m 指的是字符串的长度。
  • 查找操作：时间复杂度同样为 O (m)。
  • 空间复杂度：空间复杂度为 O (n)，n 表示所有字符串中不同字符的总数，这一特点使得 Trie 树在处理大量字符串时非常高效。

3.4.Trie 树的优缺点

优点

  • 高效前缀匹配：快速查找所有以某前缀开头的字符串（如搜索提示）。
  • 避免重复存储：共享公共前缀，节省空间。
  • 时间复杂度稳定：插入、查询、删除的时间复杂度均为 O(n)（n 为字符串长度）。

缺点

  • 空间开销大：每个字符占用一个节点，可能浪费内存（尤其是字符集大时）。
  • 实现复杂：需要处理动态节点分配和指针操作。

3.5.示例

示例一：一个字符串类型的数组arr1，另一个字符串类型的数组arr2。

  • arr2中有哪些字符串，是arr1中出现的？请打印
  • arr2中有哪些字符串，是作为arr1中某个字符串前缀出现的？请打印
  • arr2中有哪些字符串，是作为arr1中某个字符串前缀出现的？请打印arr2中出现次数最大的前缀。

实现代码如下：

#include <iostream>
#include <string>
#include <string.h>
 
using namespace std;
const int MaxBranchNum = 26;//可以扩展
 
class TrieNode{
public:
    string word;
    int path;  //该字符被划过多少次，用以统计以该字符串作为前缀的字符串的个数
    int End; //以该字符结尾的字符串
    TrieNode* nexts[MaxBranchNum];
 
    TrieNode()
    {
        word = "";
        path = 0;
        End = 0;
        memset(nexts,NULL,sizeof(TrieNode*) * MaxBranchNum);
    }
 
};
 
class TrieTree{
private:
    TrieNode *root;
public:
    TrieTree();
    ~TrieTree();
    //插入字符串str
    void insert(string str);
    //查询字符串str是否出现过，并返回作为前缀几次
    int search(string str);
    //删除字符串str
    void Delete(string str);
    void destory(TrieNode* root);
    //打印树中的所有节点
    void printAll();
    //打印以str作为前缀的单词
    void printPre(string str);
    //按照字典顺序输出以root为根的所有单词
    void Print(TrieNode* root);
    //返回以str为前缀的单词的个数
    int prefixNumbers(string str);
};
 
TrieTree::TrieTree()
{
    root = new TrieNode();
}
 
 
TrieTree::~TrieTree()
{
    destory(root);
}
 
void TrieTree::destory(TrieNode* root)
{
    if(root == nullptr)
        return ;
    for(int i=0;i<MaxBranchNum;i++)
    {
        destory(root->nexts[i]);
    }
    delete root;
    root = nullptr;
}
 
 
void TrieTree::insert(string str)
{
    if(str == "")
        return ;
    char buf[str.size()];
    strcpy(buf, str.c_str());
    TrieNode* node = root;
    int index = 0;
    for(int i=0; i<strlen(buf); i++)
    {
        index = buf[i] - 'a';
        if(node->nexts[index] == nullptr)
        {
            node->nexts[index] = new TrieNode();
        }
        node = node->nexts[index];
        node->path++;//有一条路径划过这个节点
    }
    node->End++;
    node->word = str;
}
 
int TrieTree::search(string str)
{
    if(str == "")
        return 0;
    char buf[str.size()];
    strcpy(buf, str.c_str());
    TrieNode* node = root;
    int index = 0;
    for(int i=0;i<strlen(buf);i++)
    {
        index = buf[i] - 'a';
        if(node->nexts[index] == nullptr)
        {
            return 0;
        }
        node = node->nexts[index];
    }
    if(node != nullptr)
    {
        return node->End;
    }else
    {
        return 0;
    }
}
 
void TrieTree::Delete(string str)
{
    if(str == "")
        return ;
    char buf[str.size()];
    strcpy(buf, str.c_str());
    TrieNode* node = root;
    TrieNode* tmp;
    int index = 0;
    for(int i = 0 ; i<str.size();i++)
    {
        index = buf[i] - 'a';
        tmp = node->nexts[index];
        if(--node->nexts[index]->path == 0)
        {
            delete node->nexts[index];
        }
        node = tmp;
    }
    node->End--;
}
 
int TrieTree::prefixNumbers(string str)
{
    if(str == "")
        return 0;
    char buf[str.size()];
    strcpy(buf, str.c_str());
    TrieNode* node = root;
    int index = 0;
    for(int i=0;i<strlen(buf);i++)
    {
        index = buf[i] - 'a';
        if(node->nexts[index] == nullptr)
        {
            return 0;
        }
        node = node->nexts[index];
    }
    return node->path;
}
void TrieTree::printPre(string str)
{
    if(str == "")
        return ;
    char buf[str.size()];
    strcpy(buf, str.c_str());
    TrieNode* node = root;
    int index = 0;
    for(int i=0;i<strlen(buf);i++)
    {
        index = buf[i] - 'a';
        if(node->nexts[index] == nullptr)
        {
            return ;
        }
        node = node->nexts[index];
    }
    Print(node);
}
 
void TrieTree::Print(TrieNode* node)
{
    if(node == nullptr)
        return ;
    if(node->word != "")
    {
        cout<<node->word<<" "<<node->path<<endl;
    }
    for(int i = 0;i<MaxBranchNum;i++)
    {
        Print(node->nexts[i]);
    }
}
 
void TrieTree::printAll()
{
    Print(root);
}
 
 
int main()
{
    cout << "Hello world!" << endl;
    TrieTree trie;
    string str = "li";
    cout<<trie.search(str)<<endl;
    trie.insert(str);
    cout<<trie.search(str)<<endl;
    trie.Delete(str);
    cout<<trie.search(str)<<endl;
    trie.insert(str);
    cout<<trie.search(str)<<endl;
 
    trie.insert(str);
    cout<<trie.search(str)<<endl;
 
    trie.Delete("li");
    cout<<trie.search(str)<<endl;
    trie.Delete("li");
    cout<<trie.search(str)<<endl;
    trie.insert("lia");
    trie.insert("lic");
    trie.insert("liab");
    trie.insert("liad");
    trie.Delete("lia");
    cout<<trie.search("lia")<<endl;
    cout<<trie.prefixNumbers("lia")<<endl;
 
    return 0;
}

示例二：实现 Trie 树，包含插入、查找、前缀搜索和删除功能。这个实现使用智能指针管理内存，确保内存安全。代码如下：

#include <iostream>
#include <memory>
#include <string>
#include <unordered_map>

class TrieNode {
public:
    std::unordered_map<char, std::unique_ptr<TrieNode>> children;
    bool is_end_of_word;

    TrieNode() : is_end_of_word(false) {}
};

class Trie {
private:
    std::unique_ptr<TrieNode> root;

    // 辅助函数：递归删除单词
    bool remove(TrieNode* current, const std::string& word, int index) {
        if (index == word.length()) {
            if (!current->is_end_of_word)
                return false;
            current->is_end_of_word = false;
            return current->children.empty();
        }
        char ch = word[index];
        auto it = current->children.find(ch);
        if (it == current->children.end())
            return false;
        bool shouldDeleteCurrentNode = remove(it->second.get(), word, index + 1) && !it->second->is_end_of_word;
        if (shouldDeleteCurrentNode) {
            current->children.erase(ch);
            return current->children.empty();
        }
        return false;
    }

public:
    Trie() : root(std::make_unique<TrieNode>()) {}

    // 插入单词
    void insert(const std::string& word) {
        TrieNode* current = root.get();
        for (char ch : word) {
            if (!current->children.count(ch)) {
                current->children[ch] = std::make_unique<TrieNode>();
            }
            current = current->children[ch].get();
        }
        current->is_end_of_word = true;
    }

    // 查找单词
    bool search(const std::string& word) const {
        const TrieNode* current = root.get();
        for (char ch : word) {
            auto it = current->children.find(ch);
            if (it == current->children.end())
                return false;
            current = it->second.get();
        }
        return current->is_end_of_word;
    }

    // 查找前缀
    bool startsWith(const std::string& prefix) const {
        const TrieNode* current = root.get();
        for (char ch : prefix) {
            auto it = current->children.find(ch);
            if (it == current->children.end())
                return false;
            current = it->second.get();
        }
        return true;
    }

    // 删除单词
    void deleteWord(const std::string& word) {
        remove(root.get(), word, 0);
    }
};

// 使用示例
int main() {
    Trie trie;
    
    trie.insert("apple");
    std::cout << std::boolalpha;
    std::cout << trie.search("apple") << std::endl;   // 输出: true
    std::cout << trie.search("app") << std::endl;     // 输出: false
    std::cout << trie.startsWith("app") << std::endl; // 输出: true
    
    trie.insert("app");
    std::cout << trie.search("app") << std::endl;     // 输出: true
    
    trie.deleteWord("apple");
    std::cout << trie.search("apple") << std::endl;   // 输出: false
    std::cout << trie.search("app") << std::endl;     // 输出: true
    
    return 0;
}

这个 C++ 实现具有以下特点：

  1. 内存安全：使用 std::unique_ptr 管理节点内存，避免内存泄漏
  2. 高效查找：利用 unordered_map 实现 O (1) 的子节点查找
  3. 完整功能：包含插入、查找、前缀搜索和删除操作
  4. 递归删除：删除操作会自动清理不再使用的节点

你可以根据需要扩展这个实现，例如添加统计单词数量、获取所有以特定前缀开头的单词等功能。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2376140.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

基于.Net开发的网络管理与监控工具

基于.Net开发的网络管理与监控工具

从零学习构建一个完整的系统 平常项目上线后&#xff0c;不仅意味着开发的完成&#xff0c;更意味着项目正式进入日常运维阶段。在这个阶段&#xff0c;网络的监控与管理也是至关重要的&#xff0c;这时候就需要一款网络管理工具&#xff0c;可以协助运维人员用于日常管理&…
阅读更多...
Python并发编程：开启性能优化的大门（7/10）

Python并发编程：开启性能优化的大门（7/10）

1.引言 在当今数字化时代&#xff0c;Python 已成为编程领域中一颗璀璨的明星&#xff0c;占据着编程语言排行榜的榜首。无论是数据科学、人工智能&#xff0c;还是 Web 开发、自动化脚本编写&#xff0c;Python 都以其简洁的语法、丰富的库和强大的功能&#xff0c;赢得了广大…
阅读更多...
易学探索助手-个人记录（十）

易学探索助手-个人记录（十）

在现代 Web 应用中&#xff0c;用户体验的重要性不断上升。近期我完成了两个功能模块 —— 语音播报功能 与 用户信息修改表单&#xff0c;分别增强了界面交互与用户自管理能力。 一、语音播报功能&#xff08;SpeechSynthesis&#xff09; 功能特点 支持播放、暂停、继续、停…
阅读更多...
学习51单片机01（安装开发环境）

学习51单片机01（安装开发环境）

新学期新相貌.......哈哈哈&#xff0c;我终于把贪吃蛇结束了&#xff0c;现在我们来学stc51单片机&#xff01; 要求&#xff1a;c语言的程度至少要到函数&#xff0c;指针尽量&#xff01;如果c语言不好的&#xff0c;可以回去看看我的c语言笔记。 1.开发环境的安装&#x…
阅读更多...
SpringAI

SpringAI

机器学习&#xff1a; 定义&#xff1a;人工智能的子领域&#xff0c;通过数据驱动的方法让计算机学习规律&#xff0c;进行预测或决策。 核心方法&#xff1a; 监督学习&#xff08;如线性回归、SVM&#xff09;。 无监督学习&#xff08;如聚类、降维&#xff09;。 强化学…
阅读更多...
lua 作为嵌入式设备的配置语言

lua 作为嵌入式设备的配置语言

从lua的脚本中获取数据 lua中栈的索引 3 | -1 2 | -2 1 | -3 可以在lua的解释器中加入自己自定的一些功能,其实没啥必要,就是为了可以练习下lua
阅读更多...
ERP系统源码，小型工厂ERP系统源码，CRM+OA+进销存+财务

ERP系统源码，小型工厂ERP系统源码，CRM+OA+进销存+财务

ERP系统源码&#xff0c;小型工厂ERP系统源码&#xff0c;ERP计划管理系统源码&#xff0c;CRMOA进销存财务 对于ERP来说&#xff0c;最为主要的作用就是能够强调企业的计划性&#xff0c;通过以业务订单以及客户的相关需求来作为企业计划的基础&#xff0c;并且还能够对企业现…
阅读更多...
基于EFISH-SCB-RK3576/SAIL-RK3576的矿用本安型手持终端技术方案‌

基于EFISH-SCB-RK3576/SAIL-RK3576的矿用本安型手持终端技术方案‌

&#xff08;国产化替代J1900的矿山智能化解决方案&#xff09; 一、硬件架构设计‌ ‌本安型结构设计‌ ‌防爆防护体系‌&#xff1a; 采用铸镁合金外壳复合防爆玻璃&#xff08;抗冲击能量>20J&#xff09;&#xff0c;通过GB 3836.1-2021 Ex ib I Mb认证 全密闭IP68接口…
阅读更多...
配置文件介绍xml、json

配置文件介绍xml、json

#灵感# 常用xml&#xff0c; 但有点模棱两可&#xff0c;记录下AI助理给我总结的。 .xml XML&#xff08;eXtensible Markup Language&#xff0c;可扩展标记语言&#xff09;是一种用于存储和传输数据的标记语言。它与 HTML 类似&#xff0c;但有以下主要特点和用途&#xf…
阅读更多...
【PostgreSQL数据分析实战：从数据清洗到可视化全流程】附录-D. 扩展插件列表（PostGIS/PostgREST等）

【PostgreSQL数据分析实战：从数据清洗到可视化全流程】附录-D. 扩展插件列表（PostGIS/PostgREST等）

&#x1f449; 点击关注不迷路 &#x1f449; 点击关注不迷路 &#x1f449; 点击关注不迷路 文章大纲 附录D. PostgreSQL扩展插件速查表一、插件分类速查表二、核心插件详解三、安装与配置指南四、应用场景模板五、版本兼容性说明六、维护与优化建议七、官方资源与工具八、附录…
阅读更多...
Qt笔记---》.pro中配置

Qt笔记---》.pro中配置

文章目录 1、概要1.1、修改qt项目的中间文件输出路径和部署路径1.2、Qt 项目模块配置1.3、外部库文件引用配置 1、概要 1.1、修改qt项目的中间文件输出路径和部署路径 &#xff08;1&#xff09;、为解决 “ 输出文件 ” 和 “ 中间输出文件 ”全部在同一个文件夹下的问题&am…
阅读更多...
【Liblib】基于LiblibAI自定义模型，总结一下Python开发步骤

【Liblib】基于LiblibAI自定义模型，总结一下Python开发步骤

一、前言 Liblib AI&#xff08;哩布哩布 AI&#xff09;是一个集成了先进人工智能技术和用户友好设计的 AI 图像创作绘画平台和模型分享社区。 强大的图像生成能力 &#xff1a;以 Stable Diffusion 技术为核心&#xff0c;提供文生图、图生图、图像后期处理等功能&#xff…
阅读更多...
CCF第七届AIOps国际挑战赛季军分享（RAG）

CCF第七届AIOps国际挑战赛季军分享（RAG）

分享CCF 第七届AIOps国际挑战赛的季军方案&#xff0c;从我们的比赛经历来看&#xff0c;并不会&#xff0c;相反&#xff0c;私域领域问答的优秀效果说明RAG真的很重要 历经4个月的时间&#xff0c;从初赛赛道第1&#xff0c;复赛赛道第2&#xff0c;到最后决赛获得季军&…
阅读更多...
【Cesium入门教程】第七课：Primitive图元

【Cesium入门教程】第七课：Primitive图元

Cesium丰富的空间数据可视化API分为两部分&#xff1a;primitive API面向三维图形开发者&#xff0c;更底层一些。 Entity API是数据驱动更高级一些。 // entity // 调用方便&#xff0c;封装完美 // 是基于primitive的封装// primitive // 更接近底层 // 可以绘制高级图形 /…
阅读更多...
【5分钟学Docker】Docker快速使用

【5分钟学Docker】Docker快速使用

目录 1. 概述 2. 基本操作 2.1. 镜像操作 2.2. 容器操作 2.3. 运行操作 2.4. 镜像保存 2.5. 镜像分享 3. 高级操作 4. 挂载 4.1. 目录挂载 4.2. 卷映射 1. 概述 Docker 镜像有镜像名称和TAG 2. 基本操作 2.1. 镜像操作 查看镜像 docker images docker image ls …
阅读更多...
opencv 一些简单的设置

opencv 一些简单的设置

输出当前程序启动的路径 可能会出现 &#x1f527; 设置 C17 标准&#xff08;解决 std::filesystem 报错&#xff09; 在 VS 中&#xff0c;右键项目 → 属性。 选择左边的 “C/C” → “语言” 找到 C语言标准&#xff08;C Language Standard&#xff09;选项。 设置为&…
阅读更多...
监控易运维管理软件：架构稳健，组件强大

监控易运维管理软件：架构稳健，组件强大

在当今的信息化时代&#xff0c;运维管理对于企业的稳定运营至关重要。一款好的运维管理软件&#xff0c;不仅能够帮助企业高效管理IT基础设施&#xff0c;还能提升运维效率&#xff0c;降低运维成本。今天&#xff0c;我要给大家介绍的&#xff0c;就是我们公司自主研发的监控…
阅读更多...
数字IC后端零基础入门基础理论（Day2）

数字IC后端零基础入门基础理论（Day2）

数字IC后端零基础入门基础理论&#xff08;Day1&#xff09; Placement Blockage: cell摆放阻挡层。它是用来引导工具做placement的一种物理约束或手段&#xff0c;目的是希望工具按照我们的要求来做标准单元的摆放。 它主要有三种类型&#xff0c;分别是hard placement bloc…
阅读更多...
零成本打造专属AI图像处理平台：IOPaint本地部署与远程访问指南

零成本打造专属AI图像处理平台：IOPaint本地部署与远程访问指南

文章目录 前言1.什么是IOPaint&#xff1f;2.本地部署IOPaint3.IOPaint简单实用4.公网远程访问本地IOPaint5.内网穿透工具安装6.配置公网地址7.使用固定公网地址远程访问总结 前言 移动摄影的普及使得记录生活变得轻而易举&#xff0c;然而获得一张高质量的照片往往需要付出不…
阅读更多...
操作系统-物理结构

操作系统-物理结构

操作系统使用read系统调用&#xff0c;将逻辑地址转&#xff08;对于用户来说逻辑地址容易计算&#xff0c;因为各个逻辑块都相邻&#xff09;成了逻辑块号和块内偏移量&#xff0c;并根据分配存储方式&#xff0c;将逻辑块号转成物理块号和块内偏移量 对于用户来说的文件的一…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023