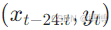设问题的数据样本点$({\mathbf{x}}_i,y_i)$，${\mathbf{x}}_i\in {\text{R}}^n$，$y_i=\pm 1$，$i=1,2,\cdots ,m$。由于标签数据 y i ∈ { − 1 , 1 } y_i\in\{-1,1\} yi​∈{−1,1}，故形成一个2-分类问题。假定特征数据 { x i } \{\boldsymbol{x}_i\} {xi​}在欧氏空间${\text{R}}^n$中按对应标签数据$y_i$的取值（-1或1）分成两个簇，如下图所示。

我们希望在两个样本点簇之间找到一个超平面$\pi$（$n=2$时为一条直线，$n=3$是为一平面）：$w_1{x}_1+w_2{x}_2+\cdots +w_n{x}_n+w_{n+1}=0$——称为分离面——将它们分开。即若$y_i=1$，则$w_1{x}_{i_1}+w_2{x}_{i_2}+\cdots +w_n{x}_{i_n}+w_{n+1}>0$。否则，$w_1{x}_{i_1}+w_2{x}_{i_2}+\cdots +w_n{x}_{i_n}+w_{n+1}<0$。若2-分类问题存在分离面，称其为线性可分的。此时，分离面往往并不唯一（见上图），希望算得最优者：每个样本点与分离面尽可能远，这样的分离面称为线性可分问题的决策面（上图中黑色的那一条）。
理论推导可得线性可分问题的决策面的系数和截距${\mathbf{w}}_0=\left(\begin{array}{c}{w}_{0_1}\\ ⋮\\ w_{0_n}\\ w_{0_{n+1}}\end{array}\right)$是二次规划
$$\{\begin{array}{l}\min \frac{1}{2}{\mathbf{w}}^{\top }\mathbf{Hw}\\ \text{s.t.}{y}_i({\mathbf{x}}_i^{\top },1)\mathbf{w}\ge 1i=1,2,\cdots ,m\end{array}$$
的最优解。其中，$\mathbf{H}=\left(\begin{array}{ccccc}1& 0& \cdots & 0& 0\\ 0& 1& \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & 1& 0\\ 0& 0& \cdots & 0& 0\end{array}\right)$。注意，$\mathbf{H}$半正定且$\frac{1}{2}{\mathbf{w}}^{\top }\mathbf{Hw}=\frac{1}{2}\sum _{i=1}^n{w}_i^2$。
样本点中，满足$y_i({\mathbf{x}}_i^{\top },1){\mathbf{w}}_0=1$的${\mathbf{x}}_i$，称为支持向量。下图展示了2维空间中线性可分问题的决策线及支持向量的实例。图中通过支持向量且平行于决策线$({\mathbf{x}}^{\top },1){\mathbf{w}}_0=0$（黑色）的直线$({\mathbf{x}}^{\top },1){\mathbf{w}}_0=\pm 1$（灰色），称为支持向量机的硬边界。不难理解，决策平面是由支持向量决定，这也是支持向量机模型名称的由来。

一旦通过训练支持向量机模型算得决策平面$\pi$：$({\mathbf{x}}^{\top },1){\mathbf{w}}_0=0$。对新的样本特征数据$\mathbf{x}$，计算
$$y=({\mathbf{x}}^{\top },1){\mathbf{w}}_0$$
若$y>0$，预测$\mathbf{x}$属于类别“1”。否则，属于类别“-1”。即以
$$\text{sign}(({\mathbf{x}}^{\top },1){\mathbf{w}}_0).$$
作为分类预测值。其中，符号函数
$$\text{sign}(x)=\{\begin{array}{ll}1& x>0\\ 0& x=0\\ -1& x<0\end{array}.$$
虽然支持向量机的作为分类器与线性回归分类器所求目标都是一个线性函数但求解机制不同，前者用决策面来分隔样本点，后者用超平面来拟合样本点。这种不同的求解机制体现在需要求解的优化问题类型的区别。下列代码实现线性可分问题的支持向量机模型。

import numpy as np														#导入numpy
from scipy.optimize import minimize										#导入minimize等
class LineSvmModel(LineModel):											#线性支持向量机模型
    def obj(self, w):													#目标函数
        return 0.5 * (np.dot(w[:(self.p - 1)], w[:(self.p - 1)]))
    def fit(self, X, Y, w = None):										#训练函数
        print("训练中...，稍候")
        m = X.shape[0]
        self.scalar = (len(X.shape) == 1)								#是否1-维样本
        self.A, self.y = self.pretreat(X, Y)							#数据预处理
        self.p = self.w0len()											#模型参数长度
        if not isinstance(w, np.ndarray):
            if w == None:
                w = np.random.random(self.p)
            else:
                w = np.array([w] * self.p)
        g = lambda x: self.y.reshape(m, 1) * self.A @ x - 1.0
        cons = {'type': 'ineq', 'fun': g}								#不等式约束
        res = minimize(self.obj, w, constraints = cons)					#计算优化模型参数
        self.w0 = res.x
        self.coef_, self.intercept_ = self.coef_inte()					#计算超平面系数和截距
        self.support_ = np.where(np.abs(Y.reshape(m, 1) * self.A\		#支持向量下标集
            @ self.w0.reshape(self.p, 1) - 1.0) < 1e-6)[0]
        print("%d次迭代后完成训练。"%res.nit)
    def ynormalize(self, y, trained):									#标签数据预处理
        if not trained:
            self.ymin=0
            self.ymax=1
        return (y-self.ymin)/(self.ymax-self.ymin)
class LineSvc(Classification, LineSvmModel):							#线性支持向量机分类器
    def __init__(self):
        self.tagVal=np.sign

程序中，

• 第3~28行定义的支持向量模型类SvmModel继承线性模型类LineModel（见博文《最优化方法Python计算：无约束优化应用——线性回归模型》）。类定义体中
  - 第4~5行定义目标函数obj，返回值为$\frac{1}{2}{\mathbf{w}}^{\top }\mathbf{Hw}$，即优化问题的目标函数。
  - 第6~24行重载训练函数fit。对比博文《最优化方法Python计算：无约束优化应用——线性回归模型》中定义的父类fit函数可见第7~16行的代码是保持一致的。第17行定义优化问题的不等式约束条件函数$\mathbf{g}(\mathbf{w})=\left(\begin{array}{c}{g}_1(\mathbf{w})\\ g_2(\mathbf{w})\\ ⋮\\ g_m(\mathbf{w})\end{array}\right)$，其中$g_i(\mathbf{w})=y_i({\mathbf{x}}_i^{\top },1)\mathbf{w}-1$，$i=1,2,\cdots ,m$。第18行构造不等式约束条件$\mathbf{g}(\mathbf{w})\ge \mathbf{o}$赋予cons，第19行调用minimize函数求解优化问题，返回值赋予res。第20行将res的x属性赋予w0。第21行调用父类的coef_inte函数（参见《最优化方法Python计算：无约束优化应用——线性回归模型》）计算决策面的系数coef_与截距intercept_。第22~23行调用Numpy的where函数，按条件
  $$y_i({\mathbf{x}}_i^{\top },1)\mathbf{w}-1\le \frac{1}{10^6},i=1,2,\cdots ,m$$
  查找支持向量的下标集并赋予属性support_。
  - 第25~29行重载标签数据归一化函数ynormalize。由于支持向量机模型中的标签数据不需要归一化，所以在训练时将self.ymin和self.ymax设置为0和1。第29行返回归一化后的标签数据。做了这样的调整，我们在进行预测操作时，式
  $$y=y\cdot (\max y-\min y)+\min y$$
  仍保持$y$的值不变，进而可保持LineModel的predict函数代码不变（参见《最优化方法Python计算：无约束优化应用——线性回归模型》）。
• 第30~32行定义的线性支持向量机分类器类LineSvc继承了Classification（见博文《最优化方法Python计算：无约束优化应用——线性回归分类器》）和LineSvmModel的属性与方法。在构造函数的第32行中将标签值函数tagVal设置为Numpy的sign函数，以便按式
  $$y=\text{sign}(({\mathbf{x}}^{\top },1){\mathbf{w}}_0)$$
  计算分类预测值。
  例1文件dataset.csv包含600个记录，每个记录由X、Y和Lable三个属性构成。其中X和Y描述样本点在平面中的笛卡尔坐标，Label表示样本分类值1或-1。前300个记录的标签值为1，后300个记录的标签为-1。

X	Y	Lable
-0.0185	1.87	1
0.147	1.99	1
-0.288	2.01	1
$\cdots$	$\cdots$	$\cdots$
2.14	-0.178	-1
2.18	0.262	-1

由X，Y作为坐标的样本在平面上的散点图如前图1所示。左上点簇的标签为1，右下点簇的标签为-1。这形成一个线性可分问题，下列代码用此数据集训练一个支持向量机模型。

import numpy as np									#导入numpy
data = np.loadtxt('dataset.csv', delimiter = ',',	#读取数据文件
                   skiprows = 1)					#去掉表头
X = np.array(data)									#转换为数组
Y = X[:, 2].astype(int)								#读取标签
X = np.delete(X, [2], axis = 1)						#删除标签数据
m, _ = X.shape[0]
print('共有%d个样本数据。'%m)
a = np.arange(m)									#下标集
np.random.seed(1006)
print('随机抽取%d个样本作为训练数据。'%(m // 10))
train = np.random.choice(a, m//10, replace=False)	#随机取得一半作为训练集下标
test = np.setdiff1d(a, train)						#测试集下标
svm = LineSvc()										#支持向量机分类模型
svm.fit(X, Y)										#训练模型
print('系数：%s'%svm.coef_)							#决策平面系数
print('截距：%.4f'%svm.intercept_)					#决策平面截距
print('支持向量下标：%s，对应的支持向量%s'%(svm.support_, X[train[svm.support_]]))
accuracy = svm.score(X, Y) * 100					#测试模型
print('分类正确率为%.2f' % (accuracy) + '%')

程序的第2~6行准备数据X和Y，读者利用代码内注释不难理解。第7~13将数据集随机地拆分成训练集X[train]，Y[train]和测试集X[yest]，Y[test]。第14行声明LineSvc类对象svm。第15行调用svm的fit函数用数据X[train]和Y[train]训练svm。第16~17行输出决策平面（直线）的系数coef_和截距intercept_。第18行输出X[train]中的支持向量下标svm.support_和对应的向量。第19行调用svm的score函数用X和Y测试svm。第20行输出测试正确率。运行程序，输出

共有600个样本数据。
随机抽取60个样本作为训练数据。
训练中...，稍候
4次迭代后完成训练。
系数：[-0.6  0.7]
截距：-0.0
支持向量下标：[26 39]，对应的支持向量[[0.2 1.7]
				      			 [1.8 0.2]]
分类正确率为100.0%

意为经过4次迭代训练所得支持向量机模型中的决策平面（直线）$\pi$：$-0.6x_1+1.7x_2=0$。两个支持向量：$(x_1,x_2)=(0.2,1.7)$和$(x_1,x_2)=(1.8,0.2)$。将它们代入决策平面可算得分别对应1和-1。对测试数据的测试正确率为100%，可见这是一个线性可分问题。

写博不易，敬请支持：
如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！