5.12 note

news2025/5/13 18:12:41

Leetcode

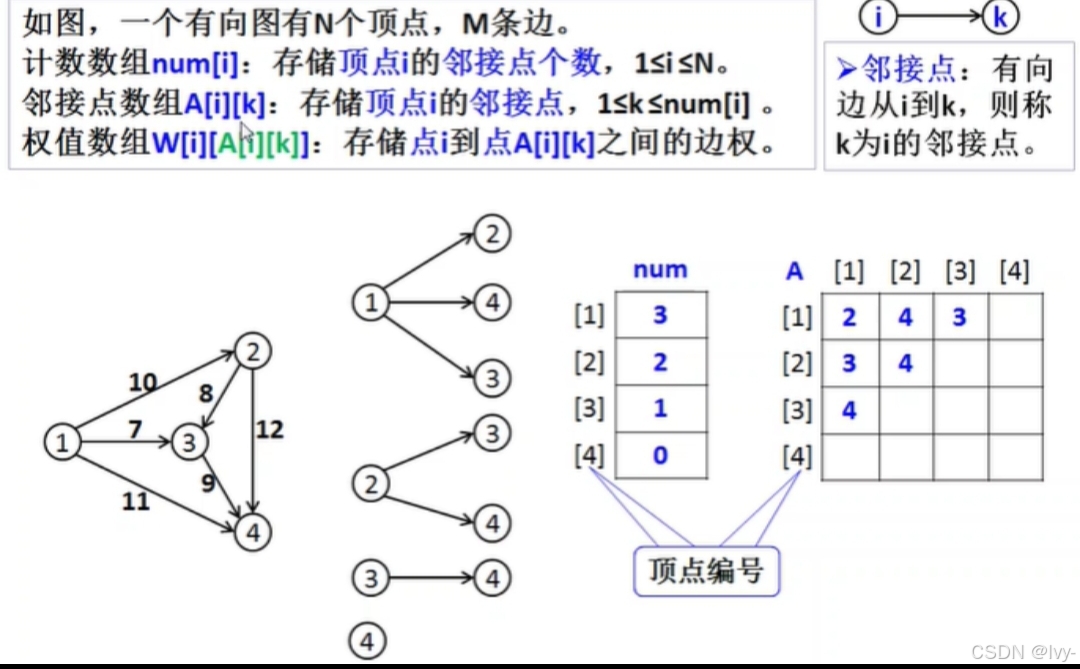
图邻接矩阵的dfs遍历

class Solution {
private:
vector<vector<int>> paths;
vector<int> path;

void dfs(vector<vector<int>>& graph, int node) {
// 到n - 1结点了保存
if (node == graph.size() - 1) {
paths.push_back(path);
return;
}
// 遍历每条能走的路
for (int i = 0; i < graph[node].size(); ++i) {
path.push_back(graph[node][i]);
dfs(graph, graph[node][i]);
// 回溯
path.pop_back();
}
}

public:
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
path.push_back(0);
// 起点能走的路
for (int i = 0; i < graph[0].size(); ++i) {
path.push_back(graph[0][i]);
dfs(graph, graph[0][i]);
path.pop_back();
}
return paths;
}
};

dfs板子

class Solution {
/*
输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]
*/

vector<string> ret;
string path;
int _n=0;

public:
vector<string> generateParenthesis(int n) {
_n=n;
dfs(0,0,0);

return ret;
}

void dfs(int i,int l,int r)
{
if(r==_n)
{
ret.push_back(path);
return;
}

if(l<_n)
{
path+="(";
dfs(i+1,l+1,r);
path.pop_back();
}
if(r<l)
{
path+=")";
dfs(i+1,l,r+1);
path.pop_back();
}
}
};

bool check全排列剪枝

前文回顾: 【[Lc_3 回溯] 决策树 | 全排列 | 子集 - CSDN App】https://blog.csdn.net/2301_80171004/article/details/146527379?sharetype=blog&shareId=146527379&sharerefer=APP&sharesource=2301_80171004&sharefrom=link

class Solution {
vector<vector<int>> ret;
bool check[7]={false};
vector<int> path;

public:
vector<vector<int>> permute(vector<int>& nums)
{
dfs(nums);
return ret;
}

void dfs(vector<int>& nums)
{
if(path.size()==nums.size())
{
ret.push_back(path);
return;
}

for(int i=0;i<nums.size();i++)
{
if(check[i]==false) //剪枝
{
path.push_back(nums[i]);
check[i]=true;//借助全局变量标记

dfs(nums); //决策树深度遍历

path.pop_back();//尾删
check[i]=false;
}
}
}
};

string resize reserve

reverse是逆转

1. 使用 resize  方法： resize  函数可以改变字符串的长度，如果新长度大于原来的长度，会在字符串末尾填充指定字符（默认为 '\0' ）；如果新长度小于原来的长度，会截断字符串。

cpp
std::string str = "hello";
str.resize(10, 'x'); // 把字符串长度调整为 10，后面填充 'x'

1. 使用 reserve  方法： reserve  函数预分配一定大小的空间，但不改变字符串的长度，主要用于提前知道字符串大概的大小，减少后续扩容的次数，提高性能。

cpp
std::string str;
str.reserve(100); // 预分配能容纳 100 个字符的空间

lambda表达式实现DFS决策的写法

class Solution {

public:

vector<string> validStrings(int n) {

vector<string> ans;

string path(n, 0);

auto dfs = [&](auto&& dfs, int i) -> void

{

if (i == n)

{

ans.push_back(path);

// 注意这里复制了一份 path，需要 O(n) 时间

return;

}

// 填 1

path[i] = '1';

dfs(dfs, i + 1);

// 填 0

if (i == 0 || path[i - 1] == '1')

{

path[i] = '0'; // 直接覆盖

dfs(dfs, i + 1);

}

};

dfs(dfs, 0);

return ans;

}

};

1. 右值引用 dfs  参数传递的设计原因：
- 在这个 Lambda 表达式 auto dfs = [&](auto&& dfs, int i) -> void  中， auto&& dfs  这种写法是为了实现递归调用。 auto&&  是一种通用引用（也叫转发引用），在这里它被用来接收函数自身（因为递归时需要调用自身）。
- 使用 auto&&  来接收 dfs  有两个好处。一方面，它可以接收左值（也就是已经存在的对象），因为递归调用时传递的 dfs  是一个已经定义好的函数对象，是左值。另一方面，它也可以完美处理一些更复杂的场景（比如在模板函数中传递函数对象等），具有更好的通用性。
- 而右值引用 &&  在这里的作用是，当调用递归函数时，它能高效地处理函数对象的传递，避免不必要的复制操作，提高程序的性能。因为 dfs  这个函数对象本身可能包含一些状态（比如捕获的外部变量 ans  和 path  ），如果每次递归调用都进行复制，会消耗额外的时间和空间。使用右值引用 &&  就可以直接传递这个函数对象的引用，而不是复制它，这样在递归调用时就更加高效了。
2.  dfs  开始执行的时机：
- 在定义完 dfs  这个 Lambda 表达式之后，代码中 dfs(dfs, 0);  这一行开始执行 dfs  函数。
- 当程序执行到 validStrings  函数的 dfs(dfs, 0);  时， dfs  函数开始第一次执行，从字符串的索引 0  位置开始进行处理。因为 0  作为参数传递给 dfs  函数的 i  参数，所以会从字符串的第一个字符开始尝试不同的取值（先设为 1  进行递归，然后在满足条件时设为 0  进行递归），进而通过递归不断地探索后续位置的字符组合情况，直到满足递归终止条件（ i == n  ）。