闫式dp分析法：

从集合角度来分析DP问题。

核心思想：

DP是一种求有限集中的最值或者个数问题

由于集合中元素的数量都是指数级别的，直接用定义去求，把每种方案都用dfs暴力枚举一遍，时间复杂度很高，此时用DP问题去优化。

DP 优化两个阶段(核心思想)

 动态规划解题步骤

步骤一：确定集合以及集合的属性

将问题看成一个集合，按照上述集合划分依据，分成若干不同子集。

按照属性定义状态，例如用 f[i] 表示考虑前 i 个元素时的某种最优解或状态。

​步骤二： 状态计算

找出状态之间的关系，即状态转移方程。这个方程描述了如何从已知子集的解构建出整个集合的解。​

步骤三：确定初始值

确定基本情况或边界条件。这些是状态转移方程中无法通过递推得到，需要直接给出的值。有时候可以直接将f数组定义为全局数组，则数组的元素会被默认初始化为0。​

例如f[0] = 0 ，表示容量为0时的最大价值为0。​

步骤四：输出结果

根据问题的要求，输出最终结果。在很多情况下，最终结果存储在 f[n] 中，其中 n 是问题的规模。​

eg:01背包问题

分析:

从2的n次方个方案中，找到总价值最大的方案，即有限集合中的最值问题，用闫式DP分析法来做。

分别求出左边的最大值，右边集合的最大值，两边取max，就是f(i,j) 的值

左边=f(i-1,j)

右边：每个方案都包含i，不变，要想值最大，需要前面变化的(1~i-1)部分最大

朴素代码

 优化空间后的代码

DP问题所有的优化都是对代码做等价变形

等价变形过程如下

 由上图分析可得，与原方程不等价。为了使之等价，可以将内层倒序循环(由大到小循环)，这样fj会比这件f(j-vi)先更新，那么此时用到的j-vi一定是上一层的，即第i-1层。

继续优化，删掉恒等式f[j]=f[j]等得到优化结果

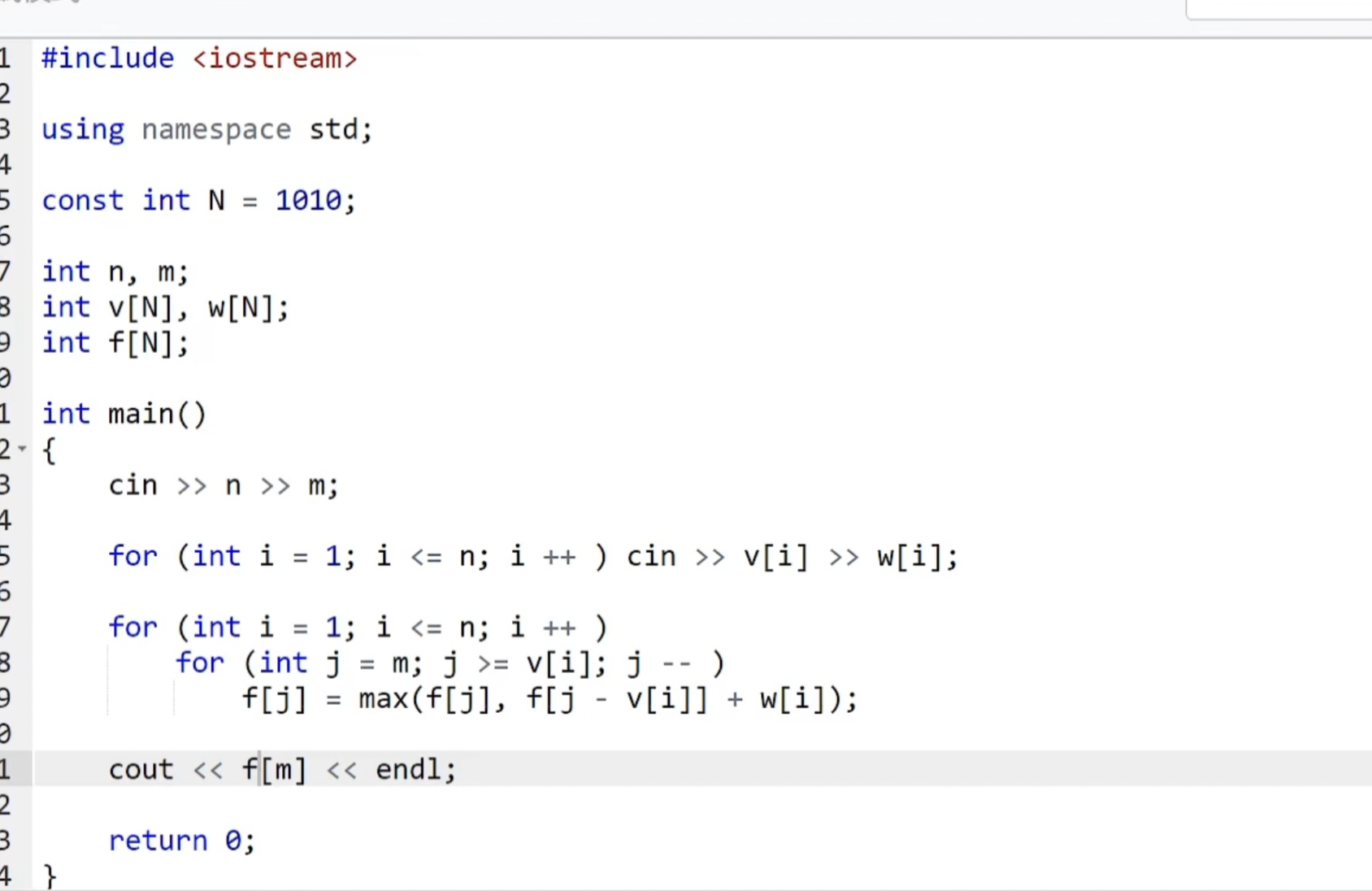
注意:

必须保证代码优化后是等价的 

内层循环：遍历每个可能的容量是为了计算在不同容量限制下的最大价值，确保我们考虑了所有可能的容量。因为在考虑第i个物品是否放入背包的时候，我们需要用当前背包的容量减去第i个物品的体积，而第i个物品的体积是任意的，因此我们需要考虑第i个物品在所有可能的容量限制下的最大价值，从而能够通过比较放入和不放入当前物品时的价值计算出在每个容量下的最大价值。

eg2:完全背包

闫式DP分析问题

 朴素代码

优化空间后的代码

按照01背包问题的方法做等价变形过程如下

 如图，恰好等价

继续优化，删掉恒等式f[j]=f[j]，将判断条件放到内层循环初始化里，因为不满足这个条件的部分会被直接跳过。

得到代码

两个问题状态转移方程如下

eg3:石子合并(区间DP问题)

分析

第一次可以选择合并的堆数是n-1，因为一共有n排，选择的相邻堆一共n-1种选法。第二次合并的时候，就剩下n-1堆，相邻两堆的个数只剩下了n-2，所以第二次合并的时候只剩下了n-2种选法，以此类推，所有不同的合并顺序一共有(n-1)！种。

满足有限集，方案很多，可以考虑DP

由分析可知，最后合并的时候一定是把左边的某一段和右边的某一段合并，因此可以分界点作为划分的依据，具体来说可以以左半边连续一段的最后一堆，如上图，最后一堆可以在第i个位置，以此类推。但至少要有两堆，所以左边这一堆最大到j-1，因此可以分成上面的j-i类。

现在只要把每一类求出来取一个min，即每个子集的min，再从这些min中取出一个最小值，就是整个集合的最小值。

最终的f[i][j]枚举k，从i到j-1 ，在里面取一个min即可。

代码

区间dp问题:先枚举区间长度，再枚举区间左端点，若区间长度为1，不用合并，所以从长度2开始枚举。

因为要在区间长度一定的情况下，在同一[i,j]区间枚举所有k的可能取值中最f[i][j]的最小值，可以先让f[i][j]等于一个正无穷，然后再枚举k

f[i][j]含义:所有将[i,j]区间合并成一堆的方案的集合中的最小值。

总体思想:把这一排石子看成一个集合，然后枚举所有可能的区间当成一个子集。在每个区间中把石子分成左右两堆，K为左右两堆的分界点，每一次枚举k，都要更新当前区间合并石子的最小值。最终根据f数组的含义，f[1][n]即为答案。

eg3:最长公共子序列

子串要求连续，子序列只要求相对顺序。

一个长度为n的序列，据每个数是在或不在这个子序列两种情况，所以一共有2的n次方个不同的子序列。暴力枚举一定会超时，所以用dp来做。

分析

按照最后一个不同点划分:第一个字符串的最后一个字符a[i]是否包含在这个子序列里，第二个字符串的最后一个字b[j]是否包含在这个字序列里来划分。a[i]和b[j]是否包含各有两种选择，所以一共是四种选择。用0表示不包含，1表示包含，前面的代表a[i]，后面的代表b[j]，四种情况如上图

对于11这种情况，只有a[i]=b[j]时才存在

对于01这种情况，f(i-1, j) 不一定会存在 bj，但已经考虑了含概 bj 可能中的最大值，虽然不含 ai 和 bj 已经在 00 中考虑了，这里就是重复，求最大最小值，重复考虑是没问题的，但是求和的时候不能重复考虑。

同理，对于10这种情况，重复考虑也是没问题。

f[i][j]含义:所有序列a[1~i]与序列b[1~j]的公共子序列的集合中，最长公共子序列的长度。

因此，f[n][m]即为最终答案。

代码

最后

我们要相信科学，不要相信玄学。

如果上述解释有不对的地方，欢迎大家指正