【递归、搜索和回溯】递归、搜索和回溯介绍及递归类算法例题

news2025/5/10 17:26:54

个人主页 ： zxctscl
专栏【C++】、【C语言】、【Linux】、【数据结构】、【算法】
如有转载请先通知

文章目录

递归、搜索和回溯
- 递归
- 搜索VS 深度优先遍历 VS 深度优先搜索 VS 宽度优先遍历 VS 宽度优先搜索 VS 暴搜
- 回溯与剪枝
1 面试题 08.06. 汉诺塔问题
- 1.1 分析
- 1.2 代码
2 21. 合并两个有序链表
- 2.1 分析
- 2.2 代码
- 2.3 总结
3 206. 反转链表
- 3.1 分析
- 3.2 代码
4 24. 两两交换链表中的节点
- 4.1 分析
- 4.2 代码
5 50. Pow(x, n)
- 5.1 分析
- 5.2 代码

递归、搜索和回溯

搜索是递归的一个分支，回溯是搜索里面的分支。

递归

什么是递归？
在数据结构二叉树、快排和归并都有提到
递归就是函数自己调用自己的情况
为什么会用到递归
二叉树的后序遍历：左子树、右子树、根
在快排中，先选择一个基准元素将数组分成两部分，左边排一下序，右边排一下序
在归并排序中，选择一个中间点，把数组平分，先让左边排一下序，再让右边排一下序，再把两个有序数组合并

递归的本质：
主问题->相同的子问题
子问题->相同的子问题
如何理解递归
（1）递归展开的细节图
（2）二叉树的题目
（3）宏观看待递归过程：
一、不要在意递归细节展开图
二、把递归的函数当成一个黑盒（具体里面如何操作的并不关心，只要能输出结果）
三、相信这个黑盒一定能完成这个任务
如何写好递归
（1）先找到相同的子问题->函数头的设计
（2）只关心某一个子问题是如何解决的->函数体的书写
（3）注意一下递归函数的出口即可

搜索VS 深度优先遍历 VS 深度优先搜索 VS 宽度优先遍历 VS 宽度优先搜索 VS 暴搜

深度优先遍历 VS 深度优先搜索->dfs
宽度优先遍历 VS 宽度优先搜索->bfs
一定程度上等同
遍历是形式，目的是搜索
关系图
暴力枚举一遍所有的结果
搜索（也叫暴搜）分为两种：dfs、 bfs
递归主要是dfs
拓展搜索问题
全排列树状图

回溯与剪枝

回溯
回溯本质就是深搜

1 面试题 08.06. 汉诺塔问题

在这里插入图片描述

1.1 分析

题目解析
中间摆放的时候必须是小盘子在大盘子的上面
算法原理
（1）如何解决汉洛塔问题？
当N=1，直接把A上面的盘子放到C上。
当N=2，想要把最大的盘子放到C上，此时先得把上面的小盘子放到B上，当把A剩下的大盘子直接移动到C上后，再将B上的小盘子放到C上。
当N=3时候，首先把A最下面盘子移动到C，前提就得将A上面的2个盘子放到B上（就像N=2时，把上面两个盘子借助C移到B上）再将A最下面的盘子放到C上，最后把B上的盘子移到C上。
当N=4时，首先把A最下面盘子移动到C，前提就得将A上面的3个盘子（当做一个整体）放到B上（就像N=3时，把上面两个盘子借助C移到B上）再将A最下面的盘子放到C上，最后把B上的盘子移到C上。
…
当N=n，也同样是首先把A最下面盘子移动到C，前提就得将A上面的n-1个盘子（当做一个整体）放到B上（就像N=n-1时，把上面两个盘子借助C移到B上）再将A最下面的盘子放到C上，最后把B上的盘子移到C上。

在这里插入图片描述
（2）为什么用递归？
大问题->相同问题的子问题
子问题->相同问题的子问题

（3）如何编写递归代码？
一、重复子问题->函数头
先把X柱子上的盘子，借助Y柱子，转移到Z柱子上
需要三个柱子，还有盘子的数量，就需要传四个参数

void dfs(X,Y,Z,int n)

二、只关心某一个子问题在做什么->函数体
（1）将X上面n-1盘子，借助Z，转移到Y上dfs(X,Z,Y,n-1)
（2）把A最下面盘子移到Z上
（3）再将Y上n-1个盘子借助X移到Z上dfs(Y,X,Z,n-1)
在这里插入图片描述

三、递归出口
当N=1时，把X上盘子放到Z上
在这里插入图片描述

编写代码
递归的细节展开图

1.2 代码

class Solution {
public:
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) 
    {      
        dfs(A,B,C,A.size());     
    }

    void dfs(vector<int>& A, vector<int>& B, vector<int>& C,int n)
    {
        if(n==1)
        {
            C.push_back(A.back());
            A.pop_back();
            return;
        }
        dfs(A,C,B,n-1);
        C.push_back(A.back());
        A.pop_back();
        dfs(B,A,C,n-1);
    }
};

2 21. 合并两个有序链表

在这里插入图片描述

2.1 分析

算法原理
解法：递归

两个链表都是升序，找两个链表头结点中较小的节点作为返回的头节点。
当选择头节点之后，就是将剩下的两个链表合并
在这里插入图片描述

（1）重复子问题->函数头
合并两个有序链表 Node*dfs(l1,l2)

（2）只关心某一个子问题在做什么事情->函数体的设计
一、比大小
二、如果l1较小：l1->next=dfs(l1->next,l2)
三、return l1

（3）递归出口

谁为空返回另一个

在这里插入图片描述

2.2 代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2)
   {
    if(list1==nullptr)return list2;
    if(list2==nullptr)return list1;

    if(list1->val<=list2->val)
    {
        list1->next=mergeTwoLists(list1->next,list2);
        return list1;
    }
    else
    {
        list2->next=mergeTwoLists(list1,list2->next);
        return list2;
    }
        
   }


};

2.3 总结

递归VS循环什么时候用循环舒服？什么时候用递归舒服？
递归和循环都是重复子问题，递归和循环之间可以相互转换

递归图越复杂，递归就越舒服

递归VS深搜
递归展开图，其实就是对一棵树做一次深度优先搜索遍历（dfs）

3 206. 反转链表

在这里插入图片描述

3.1 分析

解法：递归

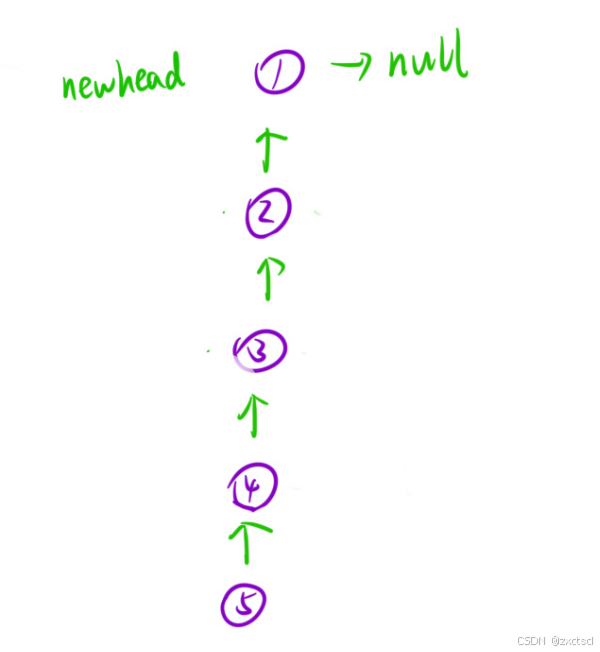
第一个视角：从宏观角度

把当前节点后面链表先逆置，并且把头结点返回；
把当前节点添加到逆置链表的后面
当遇到null就返回

第二个视角：将链表看成一棵树
先找到叶子结点，再返回
在这里插入图片描述

在这里插入图片描述

3.2 代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(head==nullptr||head->next==nullptr)return head;
        
         ListNode* newhead=reverseList(head->next);
         head->next->next=head;
         head->next=nullptr;
         return newhead;
        
    }
};

4 24. 两两交换链表中的节点

在这里插入图片描述

4.1 分析

解法：递归
视角：从宏观角度看待递归

想要两两逆置，把后面的那堆先两两逆置一下，后面的调用完dfs后，再返回后面部分的头结点，再把前面两个交换一下，把交换后的连起来。
在这里插入图片描述

在这里插入图片描述

4.2 代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if (head == nullptr || head->next == nullptr)return head;

        ListNode* tmp = swapPairs(head->next->next);
        ListNode* ret = head->next;
        head->next->next = head;
        head->next = tmp;

        return ret;
    }
};

5 50. Pow(x, n)

在这里插入图片描述

5.1 分析

解法：一、暴力循环
对于太大的幂是会超时的

二、快速幂
实现快速幂：（1）递归（2）循环

这里用递归

如果快速得到3的16次方，得到3的8次方就行，要3的8次方得到3的4次方就行，要得到3的4次方，得到3的2次方就行，要得到3，就直接3乘1就行。这里时间复杂度就是logN

那么如果除不进时，21/2除不进，就能可以分为3的10次方乘3的10次方再乘3就行，一直这样
在这里插入图片描述

（1）重复子问题->函数头

int pow(x,n)

（2）只关心某一个子问题在做什么事情->函数体的设计
先求出n/2的次方是多少: tmp=pow(x,n/2)
再判断一下n/2能不能整除，不能整除再成上x：return n%2==0?tmp*tmp*x

（3）递归出口
如果n等于0，就返回1

细节问题：

n可能是负数
要提前把负数转成正数，再用1除一下
n可能是-2^31
-2^31负数太大，转成正数会存不下，int正整数最大是2^31-1
可以提前把n的类型强转为long long

5.2 代码

class Solution {
public:
    double myPow(double x, int n) {
        return n<0?1.0/pow(x,-(long long)n):pow(x,n);
    }

    double pow(double x, int n)
    {
         if(n==0)return 1.0;
         double tmp=pow(x,n/2);
         return n%2==0?tmp*tmp:tmp*tmp*x; 
    }
};