【开源项目】Excel手撕AI算法深入理解（四）：AlphaFold、Autoencoder

项目源码地址：https://github.com/ImagineAILab/ai-by-hand-excel.git

一、AlphaFold

AlphaFold 是 DeepMind 开发的突破性 AI 算法，用于预测蛋白质的三维结构。它的出现解决了生物学领域长达 50 年的“蛋白质折叠问题”，被《科学》杂志评为 2020 年十大科学突破之首。以下从多个维度深入解析其核心原理和技术创新：

一、蛋白质折叠问题的挑战

生物学意义：蛋白质的功能由其 3D 结构决定，但实验测定（如X射线衍射、冷冻电镜）成本高且耗时。
计算复杂度：一个典型蛋白质的构象空间可达 1030010300 种，传统计算方法（如分子动力学）难以穷举。

二、AlphaFold 的技术演进

AlphaFold1（2018）

核心思想：将结构预测转化为空间约束优化问题。
关键技术：
- 使用残基间距离矩阵（distance matrix）作为预测目标。
- 结合进化信息（MSA，多序列比对）和几何约束。
- 通过梯度下降优化损失函数。
局限：依赖离散的距离区间分类，精度有限。

AlphaFold2（2020）

颠覆性创新：端到端的几何深度学习框架。
核心模块：
1. Evoformer（进化信息处理）：
  - 输入：MSA + 模板信息 → 通过自注意力机制提取协同进化信号。
  - 输出：残基对（pair）和单残基（single）的特征表示。
2. Structure Module（结构生成）：
  - 基于 SE(3)-等变网络（SE(3)-equivariant transformer），直接预测原子坐标。
  - 通过迭代优化（48次循环）逐步修正结构。
3. 损失函数：
  - 结合 FAPE（Frame-Aligned Point Error）和立体化学约束（键长/键角）。

三、关键技术创新

几何深度学习：
- 使用 SE(3)-等变网络处理三维旋转/平移对称性，避免数据冗余。
- 示例：原子坐标更新时保持物理一致性（如 Cα 骨架的刚性运动）。
注意力机制的进化：
- MSA 行注意力（捕捉同源序列关系） + 列注意力（捕捉残基间相互作用）。

在AlphaFold等蛋白质结构预测模型中，Pair Representation（配对表示） 是一种关键的数据结构，用于编码蛋白质序列中残基对（residue pairs）之间的相互作用和空间关系。它是模型理解蛋白质3D结构的核心特征之一。

2. 三角注意力（triangular attention）处理残基对的特征更新。

1. 多头注意力机制（Multi-Head Attention）

多头注意力是Transformer的核心组件，通过并行运行多个独立的注意力头，从不同角度捕捉输入数据的不同特征。

每个头（head）：是一个独立的注意力计算单元，拥有自己的权重矩阵（Query、Key、Value）。
作用：允许模型同时关注输入的不同子空间或不同特征模式（如局部/全局关系、不同语义层次等）。

公式表示：

其中，每个头的计算为：

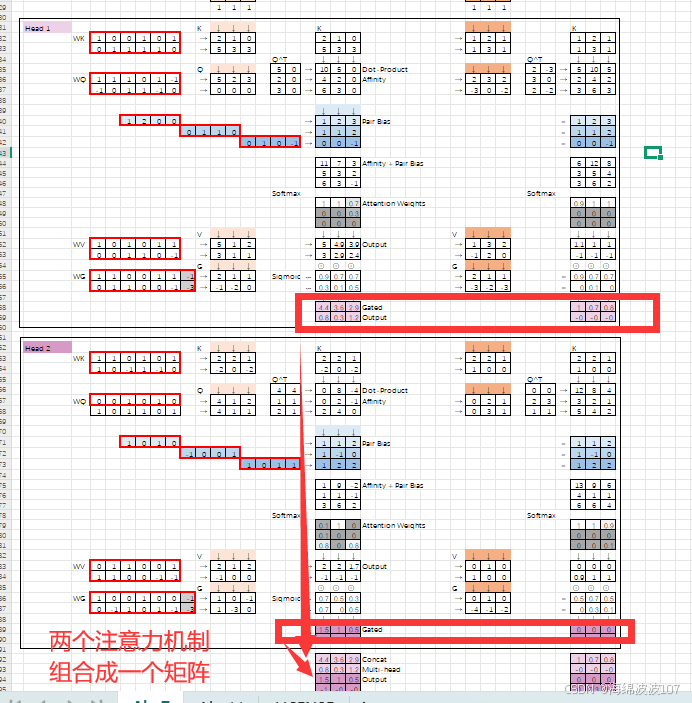
2. head1、head2 的具体含义

head1：第一个注意力头，可能专注于某种特定模式（如蛋白质序列中的局部相互作用）。
head2：第二个注意力头，可能捕捉另一种模式（如全局拓扑约束）。
在AlphaFold中，不同头可能分别关注：
- 残基间的物理距离
- 进化共变信号
- 氢键网络

3. 为什么需要多头？

并行捕捉多样性：单一注意力头可能无法同时建模复杂关系（如蛋白质中并存的局部和长程相互作用）。
增强表达能力：类似卷积神经网络中的多通道滤波。
可解释性：不同头可能学习到有明确物理意义的模式（需事后分析验证）。

可学习权重矩阵（Learnable Weight Matrices）

在深度学习和Transformer架构中（包括AlphaFold），WK、WQ、WV、WG 是注意力机制中的可学习权重矩阵（Learnable Weight Matrices），用于将输入特征映射到不同的子空间，以便计算注意力分数或生成输出。它们不是原始特征，而是模型训练中优化的参数。以下是详细解释：

1. 基本定义

这些权重矩阵属于注意力机制的核心组件，作用如下：

符号	全称	作用	维度示例
WQ	Query Weight Matrix	将输入映射到查询（Query）空间，用于计算注意力分数。	`[D_input, D_q]`
WK	Key Weight Matrix	将输入映射到键（Key）空间，与Query匹配生成相似性分数。	`[D_input, D_k]`
WV	Value Weight Matrix	将输入映射到值（Value）空间，生成注意力加权后的输出特征。	`[D_input, D_v]`
WG	Gate Weight Matrix	（可选）门控机制中的权重，控制信息流动（如AlphaFold中的门控注意力）。	`[D_input, D_g]`

输入维度：D_input（例如，AlphaFold中MSA嵌入的1280维）。
输出维度：D_q、D_k、D_v 通常相同（如64维）。

总结

WK、WQ、WV、WG 是模型参数，用于特征变换和注意力计算，而非输入特征。
它们在AlphaFold中实现：
- 进化信息的动态筛选（通过Q/K）。
- 结构约束的逐步满足（通过V）。
- 冗余信息的过滤（通过WG）。
理解这些权重的作用是剖析Transformer类模型（包括AlphaFold）的关键。

模型参数通过训练过程逐步调整

WK、WQ、WV、WG 等模型参数 正是通过训练过程逐步调整的，模型通过不断学习数据中的规律（如蛋白质的进化关系、结构约束等），最终使这些参数能够捕捉到输入特征的本质特点。

1. 模型参数的核心作用

这些权重矩阵的本质是 “可学习的特征变换器”：

动态投影：将输入特征（如氨基酸序列的嵌入向量）映射到更适合任务的空间（如关注结构相互作用的子空间）。
模式提取：通过训练自动学习哪些特征组合对预测蛋白质结构关键（例如共进化信号 vs 物理化学属性）。

类比：
想象教一个孩子识别动物：

初始时，孩子随机关注动物的颜色或形状（类似初始化的随机权重）。
通过反复观察（训练数据），他学会“耳朵形状”比“尾巴长度”更能区分猫和狗（类似权重收敛到重要特征）。

2. 参数如何学习？

(1) 训练过程

前向传播：用当前参数计算预测结构（如原子坐标）。
损失计算：比较预测与真实结构的误差（如FAPE损失）。
反向传播：通过梯度下降调整参数，降低误差。

(2) 参数更新示例（简化）

假设损失函数为 L，学习率 η：

(3) AlphaFold中的特殊优化

混合损失：同时优化结构误差（坐标偏差）和物理合理性（键长/键角）。
等变约束：确保 WQ/WK/WV 的更新不破坏SE(3)-等变性（如旋转输入时输出同步旋转）。

3. 学习到的“事物特点”示例（AlphaFold）

通过训练后，参数会编码生物学规律：

参数	可能学习到的模式	生物学对应
WQ	哪些残基应作为“查询”关注其他残基	活性位点残基的强相互作用倾向
WK	哪些残基可能作为“键”响应查询	共进化残基对的协同信号
WV	如何将注意力分数转化为结构更新信息	氢键网络的几何规则
WG	何时抑制不可靠的注意力头（如低质量MSA区域）	无序区域的噪声过滤

4. 与人类学习的对比

步骤	人类学习	模型训练
初始状态	随机猜测	参数随机初始化
反馈信号	老师纠正错误	损失函数计算预测偏差
调整方式	强化正确记忆	梯度下降更新权重
最终能力	掌握识别规则	参数固化，捕捉数据规律

四、性能与局限

准确性：
- CASP14 竞赛中 Median GDT_Score 达 92.4（>90 可视为实验精度）。
- 对部分膜蛋白和动态构象预测仍不理想。
速度：预测单个蛋白质仅需分钟级（GPU加速）。
开源影响：AlphaFold DB 已公开数百万种物种的预测结构。

二、Autoencoder

一、Autoencoder 的本质

Autoencoder 是一种无监督的神经网络，核心目的是学习数据的“高效表示”（即编码）。它由两部分组成：

Encoder（编码器）：将输入数据压缩为低维的潜在表示（latent representation）。
Decoder（解码器）：从潜在表示重建原始输入数据。

关键思想：通过迫使网络在“压缩-重建”过程中保留最关键的信息，Autoencoder 可以自动学习数据的特征。

二、Autoencoder 的结构详解

1. 输入与输出

输入：数据 x（如图像、文本向量）。
输出：重建的数据 ^x^，目标是让 ^x^ 尽可能接近 x。

2. 损失函数

通常使用 均方误差（MSE） 或 交叉熵（Cross-Entropy）：

3. 潜在空间（Latent Space）

编码器的输出是一个低维向量 =Encoder()z=Encoder(x)，称为潜在编码。
z 的维度远小于输入 x，迫使网络学习数据的本质特征。

三、Autoencoder 的变体与改进

1. 去噪自编码器（Denoising Autoencoder）

改进点：输入被添加噪声（如高斯噪声），但目标仍是重建原始干净数据。
作用：增强鲁棒性，防止简单恒等映射（即网络直接复制输入）。

2. 稀疏自编码器（Sparse Autoencoder）

改进点：在损失函数中加入稀疏性约束（如 L1 正则化）。
作用：让潜在编码 z 的大部分元素接近零，仅少数激活，模拟人脑的稀疏表征。

3. 变分自编码器（VAE, Variational Autoencoder）

改进点：将潜在编码 z 建模为概率分布（通常是高斯分布），而不仅是固定向量。
作用：支持生成新数据（通过从分布中采样 z），是生成模型的基础。

4. 卷积自编码器（Convolutional Autoencoder）

改进点：用卷积层替代全连接层，适合图像数据。
作用：保留空间局部性，更高效处理图像。

四、Autoencoder 的数学原理

以最简单的线性 Autoencoder 为例：

关键结论：若没有非线性激活且潜在维度小于输入维度，Autoencoder 等价于 PCA（主成分分析），学习的是数据的主子空间。

五、Autoencoder 的应用场景

数据降维：替代 PCA，处理非线性数据。
特征提取：预训练工具（如用编码器初始化监督任务）。
去噪：去除图像、文本中的噪声。
生成模型：VAE 能生成新样本（如人脸、音乐）。
异常检测：重建误差高的样本可能是异常值。

六、实战建议

简单实现（PyTorch 示例）：

class Autoencoder(nn.Module):
    def __init__(self, input_dim, latent_dim):
        super().__init__()
        self.encoder = nn.Sequential(
            nn.Linear(input_dim, 128), nn.ReLU(),
            nn.Linear(128, latent_dim)
        self.decoder = nn.Sequential(
            nn.Linear(latent_dim, 128), nn.ReLU(),
            nn.Linear(128, input_dim), nn.Sigmoid())
    
    def forward(self, x):
        z = self.encoder(x)
        return self.decoder(z)