前言：递归、递推是两种非常常见基础的算法了，但我之前忘了从这基础的先讲起了，大家应该也都略有了解吧！今天突然想写点相关延伸内容，所以还是完整介绍一些吧
递归
递归是一种通过函数调用自身解决问题的算法。在递归算法中，问题被分解为多个更小的子问题，这些子问题与原问题相似，但规模更小，分解的过程一直持续到到达一个基本情况，基本情况是一个可以直接解决而不需要进一步递归的简单问题。
常见的，求最大公约数就用到了递归的思想，代码如下：
#include<iostream>
using namespace std;
int gcd(int a,int b){
if(a%b==0) return b;
return gcd(b,a%b);
}
int main(){
int a,b;
cin>>a>>b;
cout<<gcd(a,b);
return 0;
} 汉诺塔问题也是非常经典的递归问题，如果你没听说过的话（“那你就out了”*bushi），网上搜一下就有，还有可视化小网站呢，输出移动过程的代码如下：
#include<iostream>
using namespace std;
void move(char x,char y){
cout<<x<<"->"<<y<<endl;
}
void Hanoi(int n,char a,char b,char c){
if(n==1){
move(a,c);
}
else{
Hanoi(n-1,a,c,b); //将n-1个盘子从A经过C移到B(从上往下都是从小到大排放)
move(a,c);
Hanoi(n-1,b,a,c);
}
}
int main(){
int n;
cin>>n; //A柱上的圆盘数
Hanoi(n,'A','B','C'); //将n个盘子从A经过B移到C
return 0;
} 噢，对了，深度优先搜索（ DFS）也是使用递归来实现的
再来道题目感觉一下吧，忘了在哪做到过的，简单说下题目大意。
题目大意：第一行n,表示数组长度,第二行输入n个非负整数,第三行输入目标值t。通过对数组中的每个数字前添加'+'或'-',构造表达式,使结果恰好等于目标值target，问共有几种组合
思路：排列组合问题，用dfs，处理n个数，每个数都可能正可能负，符合条件计数
#include<iostream>
using namespace std;
int a[20];
int n,t,count;
void dfs(int index,int sum){
if(index==n+1){
if(sum==t){
count++;
}
return;
}
dfs(index+1,sum+a[index]);
dfs(index+1,sum-a[index]);
}
int main(){
cin>>n;
for(int i=0;i<=n;i++) cin>>a[i];
cin>>t;
dfs(1,0);
cout<<count;
return 0;
} 题目：素数环 Prime Ring Problem 洛谷UVA524
思路： 用dfs，从第二个数开始填环（第一个数为1），每填一个数判断于前面数的和是否是素数并标记访问过了，最后一个数还要判断和第一个数的和是否为素数（都很简单啊，好像有点过于简单了，emm要不大白直接往后看吧）
代码：
#include<iostream>
using namespace std;
int n,t=0;
int a[20]={0,1},flag[20]={0,1};
bool ss(int x){
if(x==1) return 0;
for(int i=2;i*i<=x;i++){
if(x%i==0){
return 0;
}
}
return 1;
}
void print(){
cout<<"Case t:"<<endl;
for(int i=1;i<=n;i++){
cout<<a[i]<<" ";
}
cout<<endl;
}
void dfs(int index){
if(index==n+1){
if(ss(a[index-1]+a[1])){
print();
}
return;
}
for(int i=1;i<=n;i++){
if(!flag[i]&&(ss(i+a[index-1]))){
a[index]=i;
flag[i]=1;
dfs(index+1);
flag[i]=0;
}
}
}
int main(){
while(scanf("%d",&n)!=EOF){
for(int i=2;i<=n;i++) flag[i]=0;
t++;
dfs(2);
cout<<endl;
}
return 0;
} 还有个常见应用就是二叉树遍历了，这个在分享树的时候再一起分享吧！
递推
递推是一种通过将复杂问题分解为更简单的子问题，从子问题开始求解并将解存储起来以避免重复计算的方法。动态规划就是通过递推关系来高效地解决问题的
最基础的递推问题应该走楼梯了，代码如下：
#include<iostream>
using namespace std;
int a[51]={0,1,2};
int main(){
int n;
cin>>n;
for(int i=3;i<=n;i++){
a[i]=a[i-1]+a[i-2]; //从前一阶楼梯到i/从前两阶到i
}
cout<<a[n];
return 0;
} 要运用递推算法，非常关键的就是找到递推关系式，下面来几题感受一下，就只分析递推关系式，代码就不写了，我觉得有些题若是没遇到过还是比较难想的。以下几道题目来自B站的教学博主钉耙编程-刘春英老师的个人空间-钉耙编程-刘春英老师个人主页-哔哩哔哩视频
题目大意：1月份有一对小兔,一个月后小兔长成大兔,大兔每个月都能生一对小兔（2月1对，3月2对），问第n月有几对小兔，如5月有5对
思路：f[1]=1，f[2]=1，这个月的兔子数=上个月的兔子数+上个月的大兔数（上上个月的兔子数），所以就是斐波那契数列啦，代码我就不再写了
题目大意：一个平面上有一个圆和n条直线,每一条直线与其他直线相交,且没有3条直线交于一点,试问这些直线会将圆分成多少区域？这其实是个数学问题——n条直线最多能将一个圆分为几个部分（要想把圆分成的块数最多，那么增加的每一条线都不能过前面所有的交点）
思路：第n条直线会于其他n-1条直线相交，被分成n段,增加n个区域，所以f[n]=f[n-1]+n，其实也就是等差数列求和，结果为1+(n*(n+1))/2
题目大意：学生们站成一排,规定女生不能单独站(要么没有,要么不止一个女孩并排站),如n=4,有7种:FFFF,FFFM,MFFF,FFMM,MFFM,MMFF,MMMM 。问n个学生,有几种合法的队列数
思路：若第n个学生为男生，f[n]=f[n-1]，只要前n-1个合法就好了；若第n个学生为女生，则第n-1个学生肯定为女生，f[n]=f[n-2]+f[n-4]，前n-2个学生合法或者不合法（n-2是女生，n-3是男生）。所以结果为两种情况和f[n]=f[n-1]+f[n-2]+f[n-4]
题目大意：一行有n个方格,用红粉绿三色涂每个格子,要求任何相邻的方格不能同色,且首尾方格也不同色,求有几种涂法
思路：若前n-1个合法，则第n个方格只有一种选择；若前n-1个方格不合法(首尾同色，前n-2个合法)，则第n个方格有2种选择。所以f[n]=f[n-1]+2*f[n-2]
大家应该都知道斐波那契数列吧，就是形如f[n]=f[n-1]+f[n-2]的数列，现在介绍几种也是学习算法应该知道的数列
卡特兰数
题目：栈 洛谷P1044
思路：记入栈操作为+1，出栈操作为-1，那么合法操作序列，每个数的前缀和都应该>=0（有入栈才能出栈）。合法序列数=序列总数-不合法序列数。
主要就是一个将求不合法序列数转为求翻转后的序列数有点难以理解。将通项公式化简，也就为(2n)!/((n+1)!*n!)，可以直接代。
Cn=C从0到n-1 * C从n-1到0，还好记吧。关键是要知道题目考的是卡特兰数，这样可以帮我们简便解题。也可以计算多个不同的 n，通过观察可得，这道题的答案符合卡特兰数的规律：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012（从第0项开始），这样不用分析直接套卡特兰数的模板就行。
代码：
#include<iostream>
using namespace std;
int main(){
int n;
cin>>n;
int f[20]={1};
for(int i=1;i<=n;i++){
for(int j=0;j<i;j++){
f[i]+=f[j]*f[i-j-1];
}
}
cout<<f[n];
return 0;
} 题目：矩阵 II 洛谷P1772
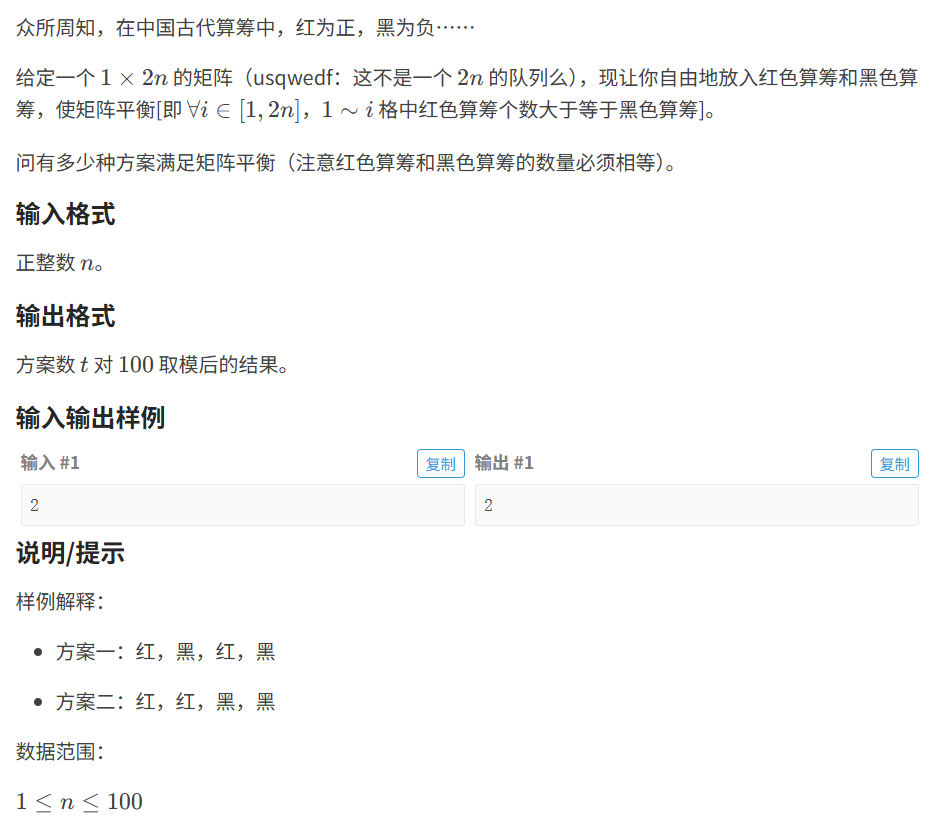思路： 这不就是上面那道题换一个说法吗？继续套模板，但注意，n=100，卡特兰数的增长是很快的，每求一项就模100
代码：
#include<iostream>
using namespace std;
int main(){
int n;
cin>>n;
long long f[101]={1};
for(int i=1;i<=n;i++){
for(int j=0;j<i;j++){
f[i]+=f[j]*f[i-j-1];
f[i]%=100;
}
}
cout<<f[n];
return 0;
} 下面这些问题的说法也都满足卡特兰数：
1.候选人A,B,n个人参加投票,投票过程中A从未落后过B(A,B最终票数相等),求投票过程的种数
2.走n*n的方格,从左上角走到右下角,只能在下三角区域(不能越过主对角线),求路程种数
3.求n个节点的二叉树的形态数
第二类斯特林数
题目：三只小猪 P3904
思路：若小猪数<房子数||房子数为0，方案数为0；若小猪数==房子数，方案数为1；若小猪数>房子数，第n只小猪可能自己一间房，或者放入任意一间已有小猪的房子，f[n][m]=f[n-1][m-1]+f[n-1][m]*n
代码：
#include<iostream>
using namespace std;
long long dp[51][51]; //dp[i][j]表示i只小猪j间房子的方案数
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
if(i==j){
dp[i][j]=1;
}else{
dp[i][j]=dp[i-1][j-1]+dp[i-1][j]*j;
}
}
}
cout<<dp[n][m];
return 0;
} 如果你知道第二类斯特林数（数据递增也是很快的，要用long long/向这种求方案数的题目最好都直接long long，防止爆int），那么又可以直接套模板秒了。
第二类Stirling数表示把n个不同的元素划分为m个非空集合的方案数，写作S ( n , m ) 。
S(n,m)=S(n−1,m−1)+S(n−1,m)∗m
将n-1个元素放入m-1个集合，第n个元素放入m集合 + n-1个元素放入m个集合，第n个元素放入m个集合的任意一个
