强化学习数学原理(三)—

强化学习数学原理(三)——值迭代

news2025/7/13 12:30:39

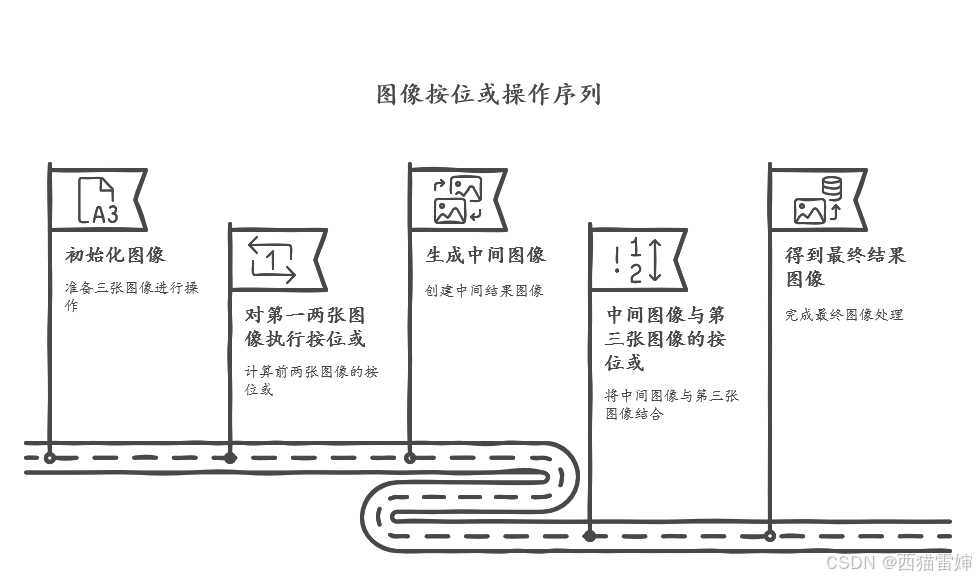
一、值迭代过程

$v=\max_\pi(r_\pi+\gamma P_\pi v)$

上面是贝尔曼最优公式，之前我们说过，f(v)=v，贝尔曼公式是满足contraction mapping theorem的，能够求解除它最优的策略和最优的state value，我们需要通过一个最优v*，这个v*来计算状态pi*，而vk通过迭代，就可以求出唯一的这个v*，而这个算法就叫做值迭代。V(s)是状态s的最优价值，R是在状态s时执行动作a可获得的，y是折扣因子(衰减系数)，还有状态概率矩阵P

1.1 初始化状态价值函数

我们说过，这个函数有两个未知量。v与pi，因此要计算最优策略，我们就需要先假设一个初始值。选择一个初始值先来表示每个状态的价值。假设我们就可以设置所有价值V(s)都为0

1.2 迭代更新价值函数

使用贝尔曼最优方程更新状态价值函数，对于与每个状态s，计算改状态下所有可能的动作a下的期望值，然后选择最大值作为新的状态价值函数。Vk是第k次迭代时s的状态，他会更新为k+1，直到k+1是最优时刻为止，具体的更新公式为：

$v_{k+1}=f(v_k)=\max_\pi(r_\pi+\gamma P_\pi v_k)$

这上面就包含了所说了两个步骤

第一步 ploicy update： $\pi_{k+1}=\arg\max_\pi(r_\pi+\gamma P_\pi v_k)$

第二部 value update： $v_{k+1}=r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}}v_k$

每次更新一个pik+1之后代入，就可以得到迭代后的vk+1，但是这里有个点，迭代过程中，左侧他是vk+1，所以他并不是我们所说的state value，他是一个值，

1.2.1 Ploicy update

$\pi_{k+1}=\arg\max_\pi(r_\pi+\gamma P_\pi v_k)$

我们把上面的公式具体的拆成每个状态对应的element，得到

$\pi_{k+1}(s)=\arg\max_{\pi}\sum_{a}\pi(a|s)\underbrace{\left(\sum_{r}p(r|s,a)r+\gamma\sum_{s^{\prime}}p(s^{\prime}|s,a)v_{k}(s^{\prime})\right)}_{q_{k}(s,a)}$

vk是已知的(假设了v0，假设现在就是v0，求pi1)，那么qk(s,a) (q1)是已知的，最优策略，就会选取qk最大时的action，其他行动为0，这样就只与q(s,a)相关，那么pik+1就知道了，就是pik+1(s)最大的一个

$\left.\pi_{k+1}(a|s)=\left\{\begin{array}{ll}1&a=a_k^*(s)\\0&a\neq a_k^*(s)\end{array}\right.\right.$

1.2.2 Value update

对于其elementwise form $v_{k+1}(s)=\sum_a\pi_{k+1}(a|s)\underbrace{\left(\sum_rp(r|s,a)r+\gamma\sum_{s^{\prime}}p(s^{\prime}|s,a)v_k(s^{\prime})\right)}_{q_k(s,a)}$

按照迭代顺序写出每一个值，从1.2.1，我们就可以知道，qk(s,a)是能求出的，注意一点，策略迭代里面，求出了最大的value对应的state，那么我们就知道这个pik+1，求出最后的结果

$v_{k+1}(s)=\max_aq_k(a,s)$

1.3 判断收敛性

每次迭代后，检查状态价值函数的变化。如果状态价值变化小于某个阈值（例如 ϵ\epsilonϵ），则认为收敛，可以终止迭代。常见的收敛条件是：

$\max_s|V_{k+1}(s)-V_k(s)|<\epsilon$

通常 $\epsilon$ 是一个小的正数，用于表示精度要求。如果状态价值函数的变化足够小，算法收敛。

根据例子，给出一个python代码

import numpy as np

# 初始化参数
gamma = 0.9  # 折扣因子
epsilon = 1e-6  # 收敛阈值
max_iterations = 1000  # 最大迭代次数
S = 4  # 状态空间大小
A = 5  # 动作空间大小

# 转移概率矩阵 P(s'|s, a) - 4x5x4 的三维矩阵
P = np.zeros((S, A, S))

## 顺时针行动
# 奖励函数 R(s, a) - 4x5 的矩阵
R = np.array([[-1, 4, -1, -1, -1],
              [-1, 4, -1, -1, -1],
              [4, -1, -1, -1, -1],
              [-1, -1, -1, -1, 1]])

# 转移概率矩阵
# 动作 a=1
P[:, 0, :] = np.array([[0.8, 0.1, 0.1, 0],
                       [0.1, 0.8, 0.1, 0],
                       [0.2, 0.2, 0.6, 0],
                       [0, 0, 0, 1]])

# 动作 a=2
P[:, 1, :] = np.array([[0.6, 0.3, 0.1, 0],
                       [0.1, 0.7, 0.2, 0],
                       [0.3, 0.3, 0.4, 0],
                       [0, 0, 0, 1]])

# 动作 a=3
P[:, 2, :] = np.array([[0.7, 0.2, 0.1, 0],
                       [0.1, 0.8, 0.1, 0],
                       [0.2, 0.2, 0.6, 0],
                       [0, 0, 0, 1]])

# 动作 a=4
P[:, 3, :] = np.array([[0.5, 0.4, 0.1, 0],
                       [0.2, 0.7, 0.1, 0],
                       [0.4, 0.4, 0.2, 0],
                       [0, 0, 0, 1]])

# 动作 a=5
P[:, 4, :] = np.array([[0.9, 0.05, 0.05, 0],
                       [0.05, 0.9, 0.05, 0],
                       [0.1, 0.1, 0.8, 0],
                       [0, 0, 0, 1]])

# 初始化状态价值函数 V(s)
V = np.zeros(S)

# 记录最优策略
pi = np.zeros(S, dtype=int)

# 值迭代算法
for k in range(max_iterations):
    V_new = np.zeros(S)
    delta = 0  # 最大值变化
    
    # 遍历每个状态
    for s in range(S):
        # 对每个动作计算期望回报
        value = -float('inf')  # 当前最大回报（初始化为负无穷）
        for a in range(A):
            # 计算该动作下的期望回报
            expected_return = R[s, a] + gamma * np.sum(P[s, a, :] * V)
            value = max(value, expected_return)  # 保持最大的期望回报
        
        # 更新当前状态的价值
        V_new[s] = value
        delta = max(delta, abs(V_new[s] - V[s]))  # 计算状态价值的变化
    
    # 更新状态价值
    V = V_new
    
    # 如果变化小于 epsilon，认为收敛
    if delta < epsilon:
        break

# 根据最优状态价值函数计算最优策略
for s in range(S):
    max_value = -float('inf')
    best_action = -1
    for a in range(A):
        # 计算每个动作下的期望回报
        expected_return = R[s, a] + gamma * np.sum(P[s, a, :] * V)
        if expected_return > max_value:
            max_value = expected_return
            best_action = a
    pi[s] = best_action

# 输出结果
print("最优状态价值函数 V*(s):")
print(V)

print("最优策略 pi*(s):")
print(pi)

MATLAB实现：

% 初始化参数
gamma = 0.9;        % 折扣因子
epsilon = 1e-6;     % 收敛阈值
max_iterations = 1000; % 最大迭代次数
S = 4;              % 状态空间大小
A = 5;              % 动作空间大小

% 转移概率矩阵 P(s'|s, a) - 4x5x4 的三维矩阵
P = zeros(S, A, S);

% 奖励函数 R(s, a) - 4x5 的矩阵
R = [-1, 4, -1, -1, -1;
     -1, 4, -1, -1, -1;
      4, -1, -1, -1, -1;
     -1, -1, -1, -1, 1];

% 转移概率矩阵
% 动作 a=1
P(:, 1, :) = [0.8, 0.1, 0.1, 0; 
              0.1, 0.8, 0.1, 0; 
              0.2, 0.2, 0.6, 0; 
              0, 0, 0, 1];
          
% 动作 a=2
P(:, 2, :) = [0.6, 0.3, 0.1, 0;
              0.1, 0.7, 0.2, 0;
              0.3, 0.3, 0.4, 0;
              0, 0, 0, 1];
          
% 动作 a=3
P(:, 3, :) = [0.7, 0.2, 0.1, 0;
              0.1, 0.8, 0.1, 0;
              0.2, 0.2, 0.6, 0;
              0, 0, 0, 1];

% 动作 a=4
P(:, 4, :) = [0.5, 0.4, 0.1, 0;
              0.2, 0.7, 0.1, 0;
              0.4, 0.4, 0.2, 0;
              0, 0, 0, 1];

% 动作 a=5
P(:, 5, :) = [0.9, 0.05, 0.05, 0;
              0.05, 0.9, 0.05, 0;
              0.1, 0.1, 0.8, 0;
              0, 0, 0, 1];

% 初始化状态价值函数 V(s)
V = zeros(S, 1);

% 记录最优策略
pi = zeros(S, 1);

% 值迭代算法
for k = 1:max_iterations
    V_new = zeros(S, 1);
    delta = 0; % 最大值变化
    
    % 遍历每个状态
    for s = 1:S
        % 对每个动作计算期望回报
        value = -Inf; % 当前最大回报（初始化为负无穷）
        for a = 1:A
            % 计算该动作下的期望回报
            expected_return = R(s, a) + gamma * sum(squeeze(P(s, a, :)) .* V);
            value = max(value, expected_return); % 保持最大的期望回报
        end
        
        % 更新当前状态的价值
        V_new(s) = value;
        delta = max(delta, abs(V_new(s) - V(s))); % 计算状态价值的变化
    end
    
    % 更新状态价值
    V = V_new;
    
    % 如果变化小于 epsilon，认为收敛
    if delta < epsilon
        break;
    end
end

% 根据最优状态价值函数计算最优策略
for s = 1:S
    max_value = -Inf;
    best_action = -1;
    for a = 1:A
        % 计算每个动作下的期望回报
        expected_return = R(s, a) + gamma * sum(squeeze(P(s, a, :)) .* V');
        if expected_return > max_value
            max_value = expected_return;
            best_action = a;
        end
    end
    pi(s) = best_action;
end

% 输出结果
disp('最优状态价值函数 V*(s):');
disp(V);

disp('最优策略 pi*(s):');
disp(pi);

修改奖励与衰减系数可得到不同V