LeetCode100之旋转图像(48)--Java

news2025/11/4 11:48:05

1.问题描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例1

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例2

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

难度等级

中等

题目链接

旋转图像

2.解题思路

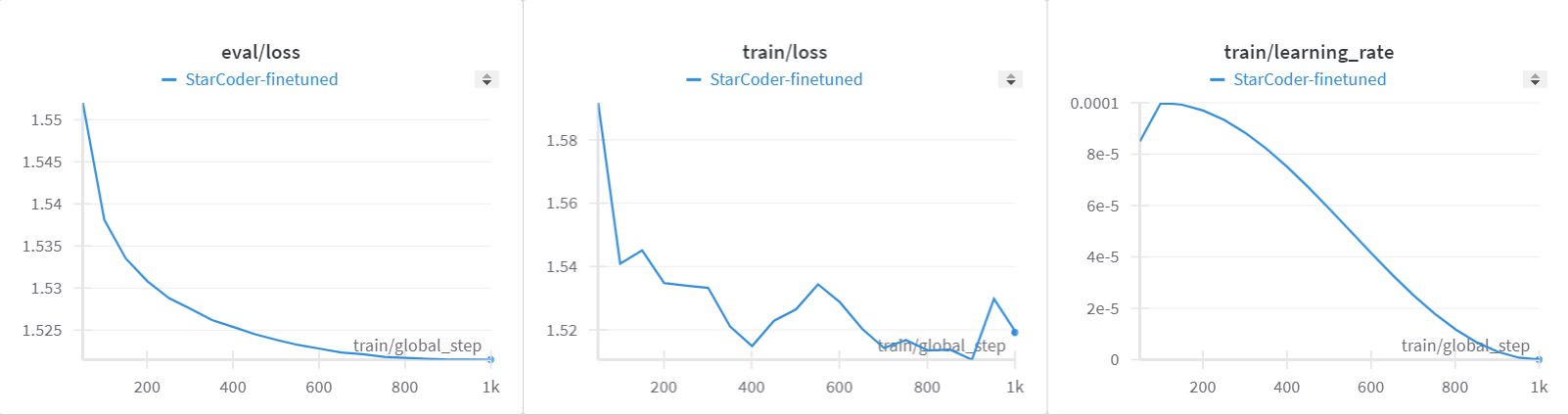
这道旋转图像的题，只要找到其中的规律，做起来十分简单。我们不难发现，这里的旋转，就是将数顺时针的转一圈，而且我们还可以发现，一个4*4的矩阵，如果将最外一层顺时针旋转一圈，我们就可以将选择一个4*4的矩阵问题，变成一个旋转3*3的矩阵问题。也就是说，我们每旋转一圈，需要旋转的矩阵就会变小，直到变成一个1*1的矩阵，无法再旋转，问题就解决了。

所以，解决这道题的关键，就是如何顺时针旋转最外层的数。这个问题也不能解决，我们可以把它分成四部分，把下面移到左边、左边移到上边、上边移到右边，右边移到下边四个部分。

我们可以定义一个layer变量来记录已经旋转的层数，我们一共要旋转n / 2层。我们每旋转一层，下一层需要旋转的个数就减少2个。

        //层数
        int layer = 0;
        while(layer < matrix.length / 2){
            //每次转移的个数
            int nums = matrix.length-1-2*layer;
            ......

}

我们要将四个方向的数进行旋转，首先得创建一个临时数据来存储其中一个方向的数，相当于把一边拆出来，然后将其它三边转一圈，然后再把拆出来的那一边安装回去。

            //创建一个临时数组
        int[] temp = new int[nums];
        //初始化临时数组(存上)
        for(int i = 0;i < nums;i++){
            temp[i] = matrix[layer][i+layer];
            
        }

我们可以就像拼积木一样，将左边的积木移动到上边。

        //左->上
        for(int i = 0;i < nums;i++){
            matrix[layer][i+layer] = matrix[matrix.length-1-i-layer][layer];
        }

再将下边的积木移动到左边。

        //下->左
        for(int i = 0;i < nums;i++){
            matrix[matrix.length - 1 -i -layer][layer] = matrix[matrix.length-1-layer][matrix.length-1-i - layer];
        }

再将右边的积木移动到下边。

        //右到下
        for(int i = 0;i < nums;i++){
            matrix[matrix.length-1-layer][matrix.length-1-i-layer] = matrix[i+layer][matrix.length-1-layer];
        }

最后再将存在临时数组中的积木(上边的)安装会右边。

        //上到右
        for(int i = 0;i < nums;i++){
            matrix[i+layer][matrix.length-1-layer] = temp[i];
        }

我们移动完一圈的积木之后，就将层数加1，变成旋转(n-1)*(n-1)的矩阵的问题。

        //层数增加
        layer++;

3.代码展示

class Solution {
    public void rotate(int[][] matrix) {
        //层数
        int layer = 0;
        while(layer < matrix.length / 2){
            //每次转移的个数
            int nums = matrix.length-1-2*layer;
            //创建一个临时数组
        int[] temp = new int[nums];
        //初始化临时数组(存上)
        for(int i = 0;i < nums;i++){
            temp[i] = matrix[layer][i+layer];
            
        }
        //左->上
        for(int i = 0;i < nums;i++){
            matrix[layer][i+layer] = matrix[matrix.length-1-i-layer][layer];
        }
        //下->左
        for(int i = 0;i < nums;i++){
            matrix[matrix.length - 1 -i -layer][layer] = matrix[matrix.length-1-layer][matrix.length-1-i - layer];
        }
        //右到下
        for(int i = 0;i < nums;i++){
            matrix[matrix.length-1-layer][matrix.length-1-i-layer] = matrix[i+layer][matrix.length-1-layer];
        }
        //上到右
        for(int i = 0;i < nums;i++){
            matrix[i+layer][matrix.length-1-layer] = temp[i];
        }
        //层数增加
        layer++;
        }
    }
}