---

前言

    算法小白初入leetcode。本文主要记录个人在leetcode上使用python解题的思路和过程，如果有更好、更巧妙的解题方法，欢迎大家在评论区给出代码或思路。🚀
    C++版可能会作为二刷放在后续的其他文章中。🧐

---

回文数

• 题目描述

1️⃣ 转成字符串

class Solution:
    def isPalindrome(self, x: int) -> bool:
        y = str(x)
        return y == y[::-1]

进阶：如果要求不能将整数转为字符串求解：

2️⃣ 求出倒序数再比对

class Solution:
    def isPalindrome(self, x: int) -> bool:
        # 负数肯定不是
        if x < 0:
            return False
        else:
            x_ = x
            y  = 0
            while x > 0:
                x, mod = divmod(x, 10)
                y = y * 10 + mod
            return y == x_                    

正则表达式匹配[hard]

• 题目描述

1️⃣ 动态规划

• 首先定义状态：令 dp[i][j]表示字符串 s 的前 i 个字符和模式 p 的前 j 个字符是否匹配。
  • dp[i][j] = true 表示 s[0:i] 和 p[0:j] 匹配。
  • dp[i][j] = false 表示 s[0:i] 和 p[0:j] 不匹配。
• 根据题意写出状态转移方程：
• 基础状态：
  • 当模式 p 和字符串 s 均为空时，dp[0][0] = true。
  • 当模式 p 为空而字符串 s 不为空时，dp[i][0] = false（模式无法匹配非空字符串）
  • 当模式 p 不为空而字符串 s 为空时讨论两种情况：1)p=*，则dp[0][j]=dp[0][j-2]；2)p!=*，此时的状态肯定是False.
• 一般状态转移：假设当前遍历到了dp[i][j]，有以下情况：
  • p[i]==s[j]或者p[i]=='.'，说明p的第i个字符和s的第j个字符可以匹配，状态转移方程为：$dp[i][j]=dp[i-1][j-1]$
  • p[i] == '*'，分成两种情况：
    • 如果p[j-1]等于s[i-1]或者p[j-1]是.，则*匹配0次：dp[i][j] = dp[i][j-2]
    • 否则，*匹配k次，匹配的过程可以这样理解，例如s='abbb',p='ab*'，k从1开始递增，这里一共需要递增3次才会匹配成功，需要比较的是s和ab,s和abb,s和abbb；这个过程反映到状态转移过程中实际上是“相反的”，k每递增一次，s就舍弃一个字母，实际上比较的是abbb和p,abb和p,a和p，最后一种情况判断时又变成了*匹配0次的情形，最终只要这几种匹配情况一种匹配上就行，所以这里的转移方程为：$dp[i][j]=dp[i][j-2]|dp[i-1][j]$

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        # 定义 dp[i][j] 表示 s 前i个字符与 p 的前j个字符是否匹配
        dp = [[False] * (len(p) + 1) for _ in range(len(s) + 1)]

        # 初始化
        dp[0][0] = True         # s、p都为空显然是返回True
        for j in range(1, len(p) + 1):  #  当s为空，p不为空时
            if p[j-1] == '*':
                dp[0][j] = dp[0][j - 2]

        # 状态转移
        for i in range(1, len(s)+1):
            for j in range(1, len(p)+1):

                # Case1
                if p[j-1] == s[i-1] or p[j-1]== '.':
                    dp[i][j] = dp[i-1][j-1]

                # Case2
                elif p[j-1] == '*':
                    if s[i-1]!= p[j-2] and p[j-2] != '.':
                        dp[i][j] = dp[i][j-2]
                    
                    else:
                        dp[i][j] = dp[i][j-2] or dp[i-1][j]
        
        return dp[len(s)][len(p)]

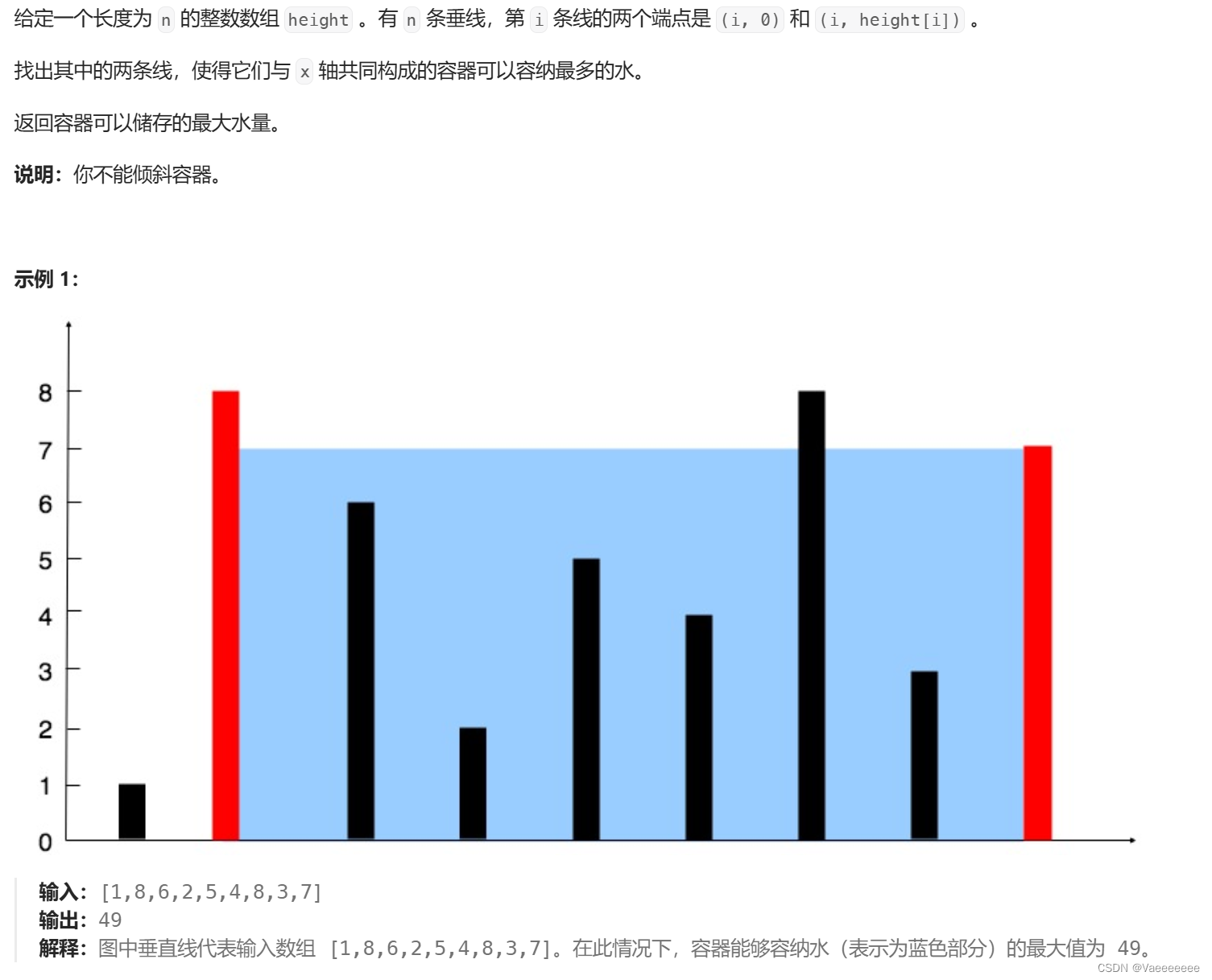
盛最多水的容器

• 题目描述

1️⃣ 遍历+分类

• 很明显可以直接遍历数组中两两组合的数字，即对应容器的两条边长，然后求出对应的储水量即可返回最后的max即可。但是这样做，遍历次数为$n(n+1)/2$，算法复杂度为$\mathcal{O}(n^2)$，最后也会超出时间限制。
• 不过想一想又会发现：在考虑1这个数字的所有可能情况时$[(1,8),(1,6),(1,2),...(1,7)]$，因为$7>1$,所以这些组合中得到的最大面积就是$(1,7)$这种情况，因为最终的面积是高度×宽度，而高度是由最短的那条边决定的，而此时的宽度就是最大的，高度最大值也就是$1$。也就是说对于考虑每个数字的所有可能情况时，从右侧往左侧遍历，如果遍历到一个比该数字还要大或等于该数字的，那么剩下的就不用考虑了。
• 那如果是在考虑$8$这个数字的所有情况呢$[(8,6),(8,2),(8,5),...(8,7)]$，由于$7<8$，此时可能会存在一个组合得到的面积比现在的面积还要大，需要继续遍历，一直到一个大于等于$8$这个数字。
• 结合上面思路，代码如下：

class Solution:
    def maxArea(self, height: List[int]) -> int:
        left = 0
        right = len(height) - 1
        re = 0
        while left < right:
            re = max(re,min(height[left],height[right])* (right - left))
            
            if height[left]*(right-left) <= re:   # 当左侧数字可能存在的最大面积都小于当前的最大面积时，直接继续下一个循环
                left += 1
                continue
            if height[right] >= height[left]:  # 右侧指针的数字比左侧大时，考虑下一个数字的情况
                left += 1
                right = len(height) - 1
                continue
            else:							# 右侧指针的数字较小时，向左移动右指针
                right -= 1
        return re

效率并不高🐢

2️⃣ 双指针+贪心

• 第一种方法是从遍历所有组合的角度出发的，如果从最大面积的角度出发可以发现，同样双指针从首尾开始移动，哪一侧的数字小，就移动哪侧的指针，因为面积是由短边决定的，如果移动数字大的那一侧指针，高度不会变化，宽度必定减少。考虑到指针是逐步向中心收缩的，意味着宽度是在逐步减少的，所以如果整个数组中的最大值×当前的宽度小于当前得到的最大面积时，可以直接返回得到的最大面积，代码如下：

class Solution:
    def maxArea(self, height: List[int]) -> int:
        left  = 0
        right = len(height)-1
        res = 0
        maximun = max(height)
        while left < right:
            
            area = min(height[left], height[right]) * (right - left)
            res = max(res, area)

            if (right-left)*maximun <= res:  # 当前情况下存在的可能最大面积如果都小于当前得到的最大值，那么后续就不用考虑了，因为宽度在减少，面积一定会减少
                break

            if height[left] < height[right]:
                left += 1
            else:
                right -= 1
        return res

快起来了🚀

最长公共前缀

• 题目描述：

1️⃣ 遍历（zip+解包）

• python做的话比较简单，直接取出对应位置的字符判断是否一致即可。

class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        min_length = min(list(map(lambda x:len(x),strs)))
        res = ''
        for i in zip(*strs):
            if len(set(i)) != 1:
                res += i[0]
            else:
                break
        return res

三数之和

• 题目描述：

1️⃣ 双指针+递归

• 思路：
  • 1、 排序：确保输入数组是排序的。如果未排序，则首先对其进行排序。
  • 2、初始化指针：设置两个指针，左指针lo初始化为 start 位置，右指针 hi 初始化为数组的最后一个元素位置（sz - 1）。
  • 3、计算当前和：计算 nums[lo] 和 nums[hi] 的和，记为 s。
  • 4、比较和与目标值：
    • 如果 s小于目标值 target，说明需要增大 s，因此移动左指针 lo 向右。
    • 如果 s大于目标值 target，说明需要减小 s，因此移动右指针 hi 向左。
    • 如果 s等于目标值 target，说明找到一个符合条件的二元组，将其加入结果列表中，然后分别移动左指针 lo 和右指针 hi，以避免重复元素。

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        nums.sort()                                   # 对输入的列表进行排序
        return self.nSumTarget(nums, 3, 0, 0)         # 这是一个通用的函数，用于找到 n 个数的和等于目标值

    def remove_duplicate_lists(self , lists: List[List[int]]) -> List[List[int]]:
        unique_lists = set(tuple(sorted(sublist)) for sublist in lists)        # 将子列表排序，并转化为元组，利用集合去重
        return [list(sublist) for sublist in unique_lists]                     # 将去重后的元组转回列表


    def nSumTarget(self, nums: List[int], n: int, start: int, target: int) -> List[List[int]]:

        '''
        nums  : 排序后的数字列表
        n     : 我们希望找到几个数的和
        start : 列表中开始计算的起始索引
        target: 我们希望凑出的目标和
        '''
        sz = len(nums)
        res = []

        # 如果找到的数字个数少于 2 或者 列表长度小于 n，则返回空结果
        if n < 2 or sz < n:
            return res

        # 两数之和是基本情况
        if n == 2:
            # 使用双指针
            lo, hi = start, sz - 1
            while lo < hi:
                s = nums[lo] + nums[hi]
                left, right = nums[lo], nums[hi]
                if s < target:
                    # 如果和小于目标值，移动左指针增大s
                    while lo < hi and nums[lo] == left:
                        lo += 1
                elif s > target:
                    # 如果和大于目标值，移动右指针减小s
                    while lo < hi and nums[hi] == right:
                        hi -= 1
                else:
                    # 如果和等于目标值，找到一个解，将其加入结果中
                    res.append([left, right])
                    while lo < hi and nums[lo] == left:         # 移动左指针以避免重复
                        lo += 1
                    while lo < hi and nums[hi] == right:        # 移动右指针以避免重复
                        hi -= 1
        else:
            # 当 n > 2 时，递归计算 (n-1)Sum 的结果
            for i in range(start, sz):
                # 递归调用，寻找 (n-1)Sum 的解
                sub = self.nSumTarget(nums, n - 1, i + 1, target - nums[i])
                for arr in sub:
                    # 将 nums[i] 加入 (n-1)Sum 的结果中，得到 nSum 的解
                    arr.append(nums[i])
                    res.append(arr)
                # 跳过重复的元素，以避免重复解
                while i < sz - 1 and nums[i] == nums[i + 1]:
                    i += 1
        return self.remove_duplicate_lists(res)

最接近的三数之和

• 题目描述

1️⃣ 迭代一次+双指针

• 思路和三数之和的思路一致，这类问题都可以用这种方法通解。直接看代码：

class Solution:
    def threeSumClosest(self, nums: List[int], target: int) -> int:
        # 循环 + 双指针
        if len(nums) < 3:
            return None
        
        # 首先排序
        nums.sort()
        difference = float('inf')  # 最接近的值和目标值之间的差值

        for i in range(len(nums) - 2):
            # 当其中一个数为nums[i]时，找出最接近的三数之和，此时通过另一个函数找出最接近的两数之和
            sum = nums[i] + self.twoSumClosest(nums[i+1:], target - nums[i])

            if abs(target - sum) < abs(difference):
                difference = target - sum
        return target - difference
    
    def twoSumClosest(self, num, target):
        left, right = 0, len(num) -1
        difference = float('inf')
        while left < right:
            sum = num[left] + num[right]
            if abs(target - sum) < abs(difference):
                difference = target - sum
            if sum < target:
                left += 1
            else:
                right -=1
        return target - difference

电话号码的字母组合

1️⃣ 常规方法：暴力循环

• 常规方法非常好理解：每次取出一个数字，该数字对应的所有字母与之前的结果进行组合，直到遍历所有数字即可。

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        num_to_char = {
            "2": ['a', 'b', 'c'], "3": ['d', 'e', 'f'], "4":['g', 'h', 'i'] , 
            "5": ['j', 'k', 'l'], "6": ['m', 'n', 'o'], "7":['p', 'q', 'r', 's'] , 
            "8": ['t', 'u', 'v'], "9": ['w', 'x', 'y', 'z']}
        res = []
        res = ['']
        while digits:
            
            cur_res = num_to_char[digits[-1]]
            res     = list(map(lambda x: x[0] + x[1], [(i, j) for i in cur_res for j in res]))
            digits  = digits[:-1]

        if res == ['']:
            res = []
        return res 

2️⃣ 回溯法

• 内容参考：回溯算法解题套路框架
• 回溯算法都是在遍历一棵树，树的叶子节点对应着其中一个解。
  • 输入的第一个数字开始，依次遍历每个字母。
  • 对于每个字母，进入下一层递归处理下一个数字。
  • 如果已经处理完所有的数字（递归到底），说明已经生成了一个有效的字母组合，记录下
    来。

代码：

class Solution:
    
    def __init__(self):
        self.result = []  # 保存结果，即存储所有字母组合

    def letterCombinations(self, digits: str) -> List[str]:
        num_to_char = {
        "2": ['a', 'b', 'c'], "3": ['d', 'e', 'f'], "4":['g', 'h', 'i'], 
        "5": ['j', 'k', 'l'], "6": ['m', 'n', 'o'], "7":['p', 'q', 'r', 's'] , 
        "8": ['t', 'u', 'v'], "9": ['w', 'x', 'y', 'z']}
        
        def backtrack(index, path):
            # 确定结束条件
            if index == len(digits):
                self.result.append(''.join(path))
                return
            # 当前数字对应的所有字母
            current_chars = num_to_char[digits[index]]

            for char in current_chars:
                # 做选择
                path.append(char)

                # 递归处理下一个数字
                backtrack(index + 1, path)

                # 撤销选择
                path.pop()

        if not digits:
            return []
        backtrack(index=0, path=[])  # 从第一个数字开始，路径初始化为空
        return self.result

合并两个有序链表

• 题目描述

1️⃣ 双指针

• 两个指针从各自链表的头结点开始移动，比较对应的值，将更小的数放到新链表中即可，一直到两个链表中元素都遍历完。
• 在链表中如果涉及到新链表时，可以使用虚拟头结点这个技巧。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        head = ListNode(-1)  # 虚拟头结点
        ptr  = head
        ptr1 = list1
        ptr2 = list2

        while ptr1  and ptr2 :
            # 比较两个指针的值，选择较小的值添加到新链表
            if ptr1.val < ptr2.val:
                ptr.next = ptr1
                ptr1     = ptr1.next
            else:
                ptr.next = ptr2
                ptr2     = ptr2.next
                
            ptr = ptr.next

        if ptr1:
            ptr.next = ptr1
        if ptr2:
            ptr.next = ptr2

        return head.next

2️⃣ 递归

• 这一题递归理解写起来并不算难：比较两个节点值的大小，如果list1<list2，就把list1下一个节点和list2放到这个函数中进行递归；反之，就把list2下一个节点和list1放到这个函数中进行递归，代码如下：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        
        if not list1:
            return list2
        if not list2:
            return list1

        if list1.val < list2.val:
            list1.next = self.mergeTwoLists(list1.next, list2)
            return list1
        else:
            list2.next = self.mergeTwoLists(list1, list2.next)
            return list2    

总结

算法小白初入leetcode，期待给出更精妙的算法🚀🚀🚀