原样输出

题目：给定一个数n，请原样输出

输入：输入只有一个数，可能为小数，也可能为整数，-1000000<n<1000000

输出：原样输出

输入：1.123

输出：1.123

import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        System.out.println(String.valueOf(n));
    }
}

数塔

题目：在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的：

有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

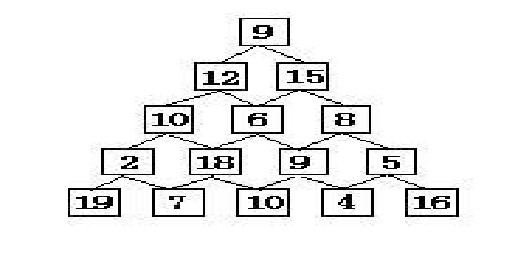
已经告诉你了，这是个DP的题目，你能AC吗?

输入：输入数据首先包括一个整数C,表示测试实例的个数，每个测试实例的第一行是一个整数N(1 <= N <= 100)，表示数塔的高度，接下来用N行数字表示数塔，其中第i行有个i个整数，且所有的整数均在区间[0,99]内

输出：对于每个测试实例，输出可能得到的最大和，每个实例的输出占一行

输入：

1 5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5

输出：30

//数塔问题
public class Main3 {
 
    public static void main(String[] args) {
        int[][] arr = { {8,  0,  0,  0,  0},
                        {12, 15, 0,  0,  0},
                        {3,  9,  6,  0,  0},
                        {8, 10,  5,  12, 0},
                        {16, 4,  18, 10, 9},
                             };
        int res =  getMaxSum(arr);
        System.out.println("最大路径值为："+res);
    }
 
    public static int getMaxSum(int [][] arr){
        int n = arr.length;
        int[][] maxSum=new int[n][n];
 
        //初始化最后一行
        for (int i = 0; i <n ; i++) {
            maxSum[n-1][i] = arr[n-1][i];
        }
        for (int i = n-2; i >=0; i--) {
            for (int j = 0; j <n-1 ; j++) {
                maxSum[i][j] = Math.max(maxSum[i+1][j]+arr[i][j],maxSum[i+1][j+1]+arr[i][j]);
            }
        }
 
        //保存路径
        List<Integer> path = new ArrayList<Integer>();
 
        int max = maxSum[0][0];
        for (int i = 0; i<n-1; i++) {
            for (int j = 0; j <=i ; j++) {
               if ((max-arr[i][j])==maxSum[i+1][j+1]){
                   max = maxSum[i+1][j+1];
                   path.add(arr[i][j]);
                   break;
               }else if ((max-arr[i][j])==maxSum[i+1][j]){
                   max = maxSum[i+1][j];
                   path.add(arr[i][j]);
                   break;
                }
            }
        }
        //添加最后一层
        for (int i = 0; i <n ; i++) {
            if (arr[n-1][i]==max){
                path.add(arr[n-1][i]);
            }
        }
        //打印路径
        for (int i = 0; i < path.size(); i++) {
            System.out.print(path.get(i)+"-->");
        }
        System.out.println("");
        return maxSum[0][0];
    }
}