环形链表I

点击链接做题

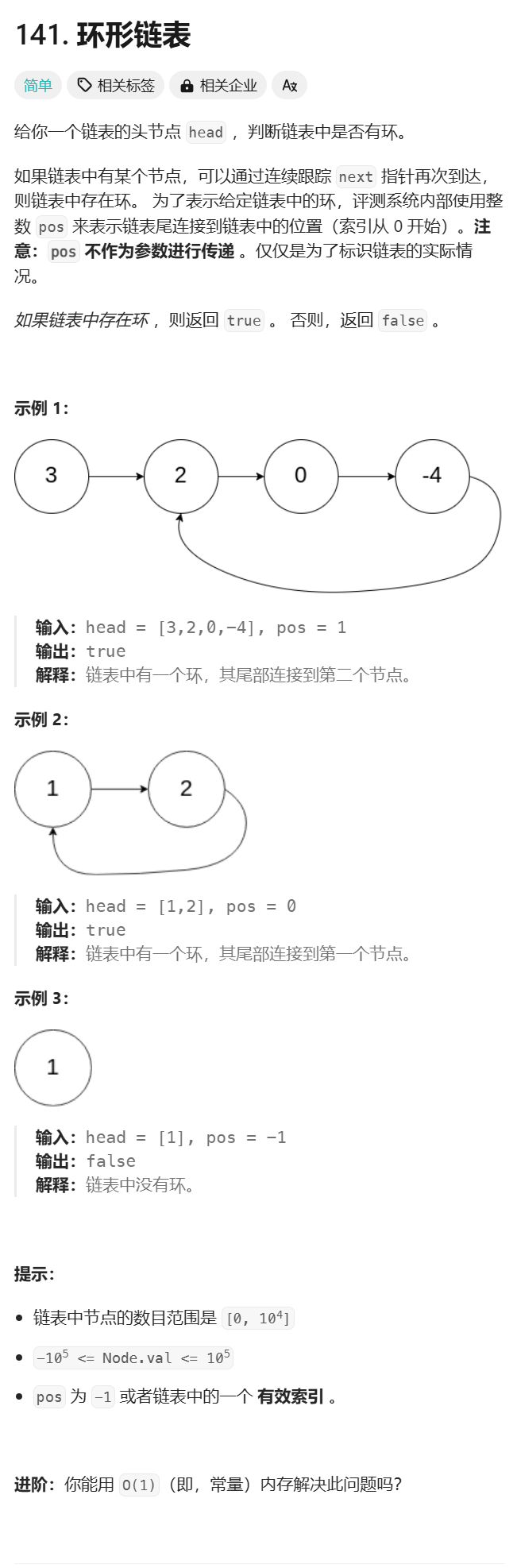
思路：快慢指针

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) {
    //快慢指针
    ListNode* slow = head;
    ListNode* fast = head;
    while(fast && fast->next){
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast){
            return true;
        }
    }
    //两个指针始终没有相遇
    return false;
}

---

思考1：为什么快指针每次走两步，慢指针走一步可以相遇，有没有可能遇不上，请推理证明！

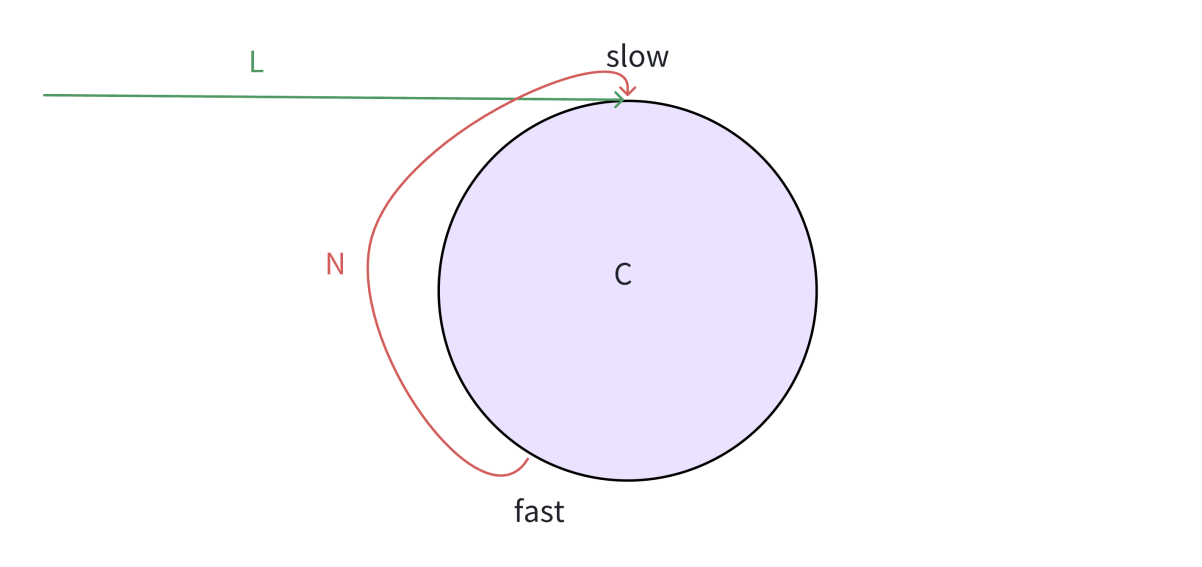
slow一次走1步，fast一次走2步，fast先进环，假设slow也走完入环前的距离，准备进环，此时fast和slow之间的距离为N，接下来的追逐过程中，每追击一次，他们之间的距离缩小1步

因此，在带环链表中慢指针走一步，快指针走两步最终一定会相遇。

思考2：快指针一次走3步，走4步，...n步行吗?

step1:

按照上面的分析，慢指针每次走一步，快指针每次走三步，此时快慢指针的最大距离为N，接下来的追逐过程中，每追击一次，他们之间的距离缩小2步追击过程中fast和slow之间的距离变化：

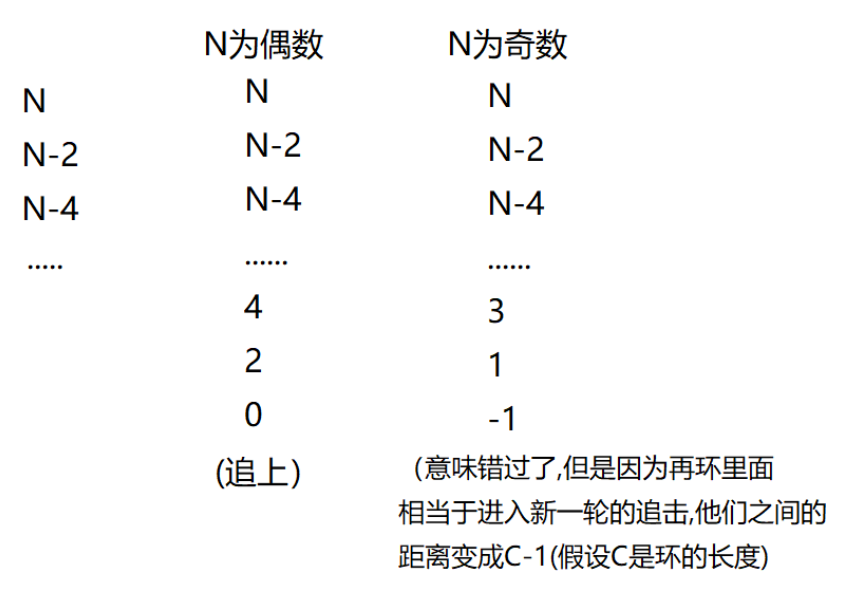
分析:

1. 如果N是偶数，第一轮就追上了

2. 如果N是奇数，第一轮追不上，快追上，错过了，距离变成-1，即C-1，进入新的一轮追击

   a. C-1如果是偶数，那么下一轮就追上了

   b. C-1如果是奇数，那么就追不上，进入新的一轮追击

总结一下追不上的前提条件：N是奇数，C是偶数

step2：

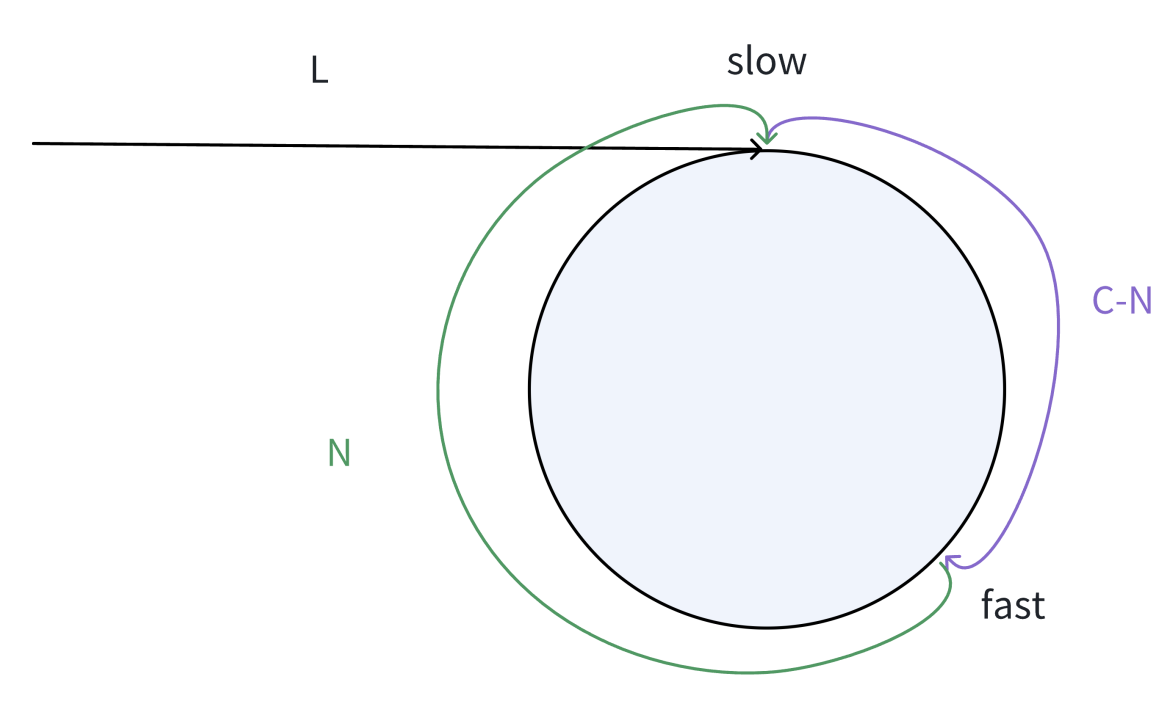
假设：

环的周长为C，头结点到slow结点的长度为L，slow走一步，fast走三步，当slow指针入环后，slow和fast指针在环中开始进行追逐，假设此时fast指针已经绕环x周。

在追逐过程中，快慢指针相遇时所走的路径长度:

fast: L+xC+C-N

slow：L

由于慢指针走一步，快指针要走三步，因此得出： 3 * 慢指针路程 = 快指针路程 ，即：

3L = L + xC + C − N （化简前）

2L = (x + 1)C − N （化简后）

对上述公式继续分析：由于偶数乘以任何数都为偶数，因此2L一定为偶数，则可推导出可能得情况：

• 情况1：偶数 = 偶数 - 偶数

• 情况2：偶数 = 奇数 - 奇数

由step1中（1）得出的结论，如果N是偶数，则第一圈快慢指针就相遇了。

由step1中（2）得出的结论，如果N是奇数，则fast指针和slow指针在第一轮的时候套圈了，开始进行下一轮的追逐；当N是奇数，要满足以上的公式，则 (x+1)C 必须也要为奇数，即C为奇数，满足（2）a中的结论，则快慢指针会相遇

因此， step1 中的 N是奇数，C是偶数不成立 ，既然不存在该情况，则快指针一次走3步最终一定也可以相遇。

快指针一次走4、5…步最终也会相遇，其证明方式同上。

---

提示：

虽然已经证明了快指针不论走多少步都可以满足在带环链表中相遇，但是在编写代码的时候会有额外的步骤引入，涉及到快慢指针的算法题中通常习惯使用慢指针走一步快指针走两步的方式。