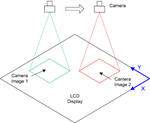
各向异性含水层中地下水三维流基本微分方程的推导
参考文献:
- [1] 刘欣怡,付小莉.论连续性方程的推导及几种形式转换的方法[J].力学与实践,2023,45(02):469-474.
文章链接
水均衡的基本思想: ∑ 流 入 − ∑ 流 出 = Δ V \sum 流入-\sum 流出=\Delta V ∑流入−∑流出=ΔV
在渗流场中取任意一点 P ( x , y , z ) P(x,y,z) P(x,y,z),设单元体无限小,但保证单元体中地下水穿过介质骨架和孔隙,设 Δ z \Delta z Δz, Δ x , Δ y \Delta x, \Delta y Δx,Δy为常量,水的密度为 ρ \rho ρ,孔隙度 n n n,单元体高度 Δ z \Delta z Δz
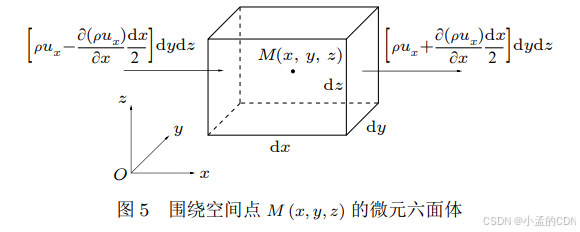
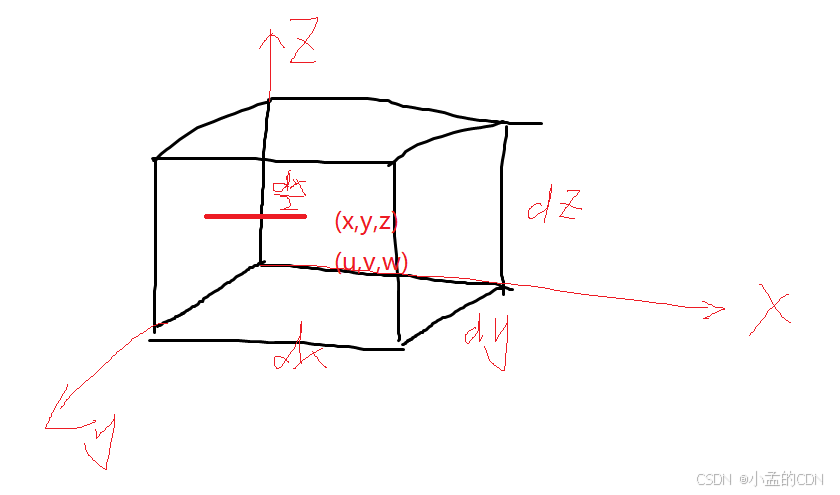
中心点的坐标:
(
x
,
y
,
z
)
(x,y,z)
(x,y,z)
中心点的流速:
(
u
,
v
,
w
)
(u, v,w)
(u,v,w)
d y d z dydz dydz是流入方向垂直的面积 S S S,
微元体内质量的时间变化率可以表示为: d M d t = 质 量 × 密 度 时 间 = ρ V d t = ∂ ρ d x d y d z ∂ t \frac{dM}{dt}=\frac{质量×密度}{时间}=\frac{\rho V}{dt}=\frac{\partial \rho \ dxdydz}{\partial t} dtdM=时间质量×密度=dtρV=∂t∂ρ dxdydz
已知泰勒公式:
f
(
x
)
=
f
(
x
0
)
+
f
(
x
0
)
′
1
!
(
x
−
x
0
)
+
.
.
.
.
+
f
n
(
x
0
)
n
!
(
x
−
x
0
)
n
f(x)=f(x_0)+\frac{f(x_0)'}{1!}(x-x_0)+....+\frac{f^n(x_0)}{n!}(x-x_0)^n
f(x)=f(x0)+1!f(x0)′(x−x0)+....+n!fn(x0)(x−x0)n
对照泰勒公式,流入左侧面的速度为:
u x − ∂ u x ∂ x ( d x − d x 2 ) u_x-\frac{\partial u_x}{\partial x}(dx-\frac{dx}{2}) ux−∂x∂ux(dx−2dx)
某一断面的流量等于流速
v
v
v与断水面积的乘积
A
A
A
A
=
v
A
A=v A
A=vA
流体力学中的质量流率计算:在流体力学中,密度速度面积乘积可以用来计算流体通过某个截面的质量流率。质量流率是单位时间内通过某个截面的质量,可以用公式m=pvA来计算,其中m表示质量。
质
量
=
密
度
×
流
速
×
面
积
×
时
间
质量=密度×流速×面积×时间
质量=密度×流速×面积×时间
两边同时乘以
ρ
\rho
ρ
ρ
u
x
−
∂
ρ
u
x
∂
x
d
x
2
\rho u_x-\frac{\partial \rho u_x}{\partial x}\frac{dx}{2}
ρux−∂x∂ρux2dx
流出右侧的速度为:
ρ
u
x
+
∂
ρ
u
x
∂
x
d
x
2
\rho u_x+\frac{\partial \rho u_x}{\partial x}\frac{dx}{2}
ρux+∂x∂ρux2dx
再乘以面积 d y d z dydz dydz,以流出量减去流入量得到:
ρ u x + ∂ ρ u x ∂ x d x 2 − ρ u x − ∂ ρ u x ∂ x d x 2 = ∂ ρ d x d y d z ∂ t \rho u_x+\frac{\partial \rho u_x}{\partial x}\frac{dx}{2}-\rho u_x-\frac{\partial \rho u_x}{\partial x}\frac{dx}{2}=\frac{\partial \rho \ dxdydz}{\partial t} ρux+∂x∂ρux2dx−ρux−∂x∂ρux2dx=∂t∂ρ dxdydz