LeetCode题练习与总结：排序链表--148

news2025/4/5 18:30:51

一、题目描述

给你链表的头结点 head ，请将其按升序排列并返回 排序后的链表 。

示例 1：

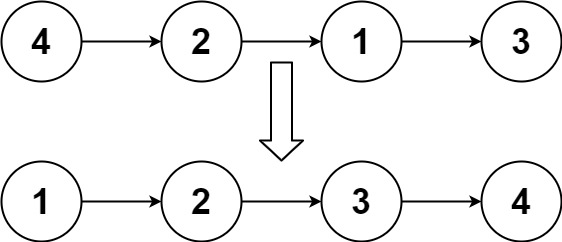
输入：head = [4,2,1,3]
输出：[1,2,3,4]

示例 2：

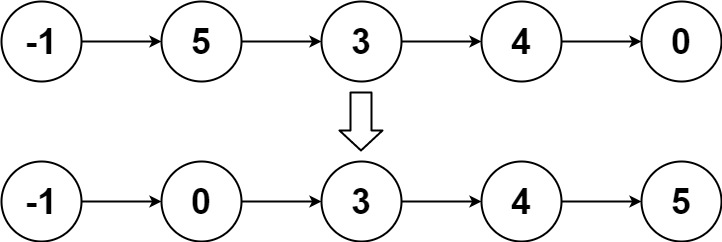
输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

示例 3：

输入：head = []
输出：[]

提示：

链表中节点的数目在范围 [0, 5 * 10^4] 内
-10^5 <= Node.val <= 10^5

二、解题思路

要解决这个问题，我们可以使用归并排序，这是一种适合链表的排序算法，因为链表的元素在内存中不是连续存储的，归并排序不需要额外的存储空间，且时间复杂度为O(n log n)，是一种效率较高的排序算法。

归并排序的基本思想是将链表分成两半，分别对这两半进行排序，然后将排序好的两部分合并在一起。在链表中实现这一思想相对简单，因为只需要改变节点的next指针即可完成排序。

以下是使用归并排序对链表进行排序的步骤：

找到链表的中点，可以使用快慢指针法。
将链表从中点断开，形成两个子链表。
对两个子链表分别进行递归排序。
将两个已排序的子链表合并在一起。

三、具体代码

class Solution {
    public ListNode sortList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        // Step 1. 分割链表
        ListNode slow = head, fast = head.next;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        ListNode mid = slow.next;
        slow.next = null;

        // Step 2. 递归排序
        ListNode left = sortList(head);
        ListNode right = sortList(mid);

        // Step 3. 合并链表
        return merge(left, right);
    }

    private ListNode merge(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(0);
        ListNode current = dummy;
        while (l1 != null && l2 != null) {
            if (l1.val < l2.val) {
                current.next = l1;
                l1 = l1.next;
            } else {
                current.next = l2;
                l2 = l2.next;
            }
            current = current.next;
        }
        if (l1 != null) {
            current.next = l1;
        } else {
            current.next = l2;
        }
        return dummy.next;
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

分割链表：使用快慢指针找到中点的时间复杂度是O(n)，其中n是链表的长度。
递归排序：将链表分割成两半，每半的长度大约是n/2，因此递归的深度是O(log n)，每次递归调用需要对两个子链表进行合并，合并的时间复杂度是O(n)，所以递归排序的总时间复杂度是O(n log n)。
合并链表：合并两个有序链表的时间复杂度是O(n)，因为每个节点最多被访问一次。
综上所述，整个算法的时间复杂度是O(n log n)。

2. 空间复杂度

递归栈空间：由于归并排序是递归进行的，所以需要递归栈空间。递归的最大深度是O(log n)，每个递归调用需要常数空间，所以递归栈空间的总空间复杂度是O(log n)。
合并链表：合并链表时，除了输入的链表节点外，只需要一个哑节点和几个指针，不需要额外的空间，因此合并链表的空间复杂度是O(1)。
综上所述，整个算法的空间复杂度是O(log n)，主要取决于递归栈的空间消耗。

综合以上分析，归并排序链表的算法时间复杂度是O(n log n)，空间复杂度是O(log n)。