目录

1. 二维随机向量(X,Y)的数学期望EX, EY

2. 二维随机向量函数z=g(X,Y)的数学期望EZ

3. 二维随机向量(X,Y)的方差DX, DY

4. 二维随机向量的性质（和、积的数学期望E与方差D）

5. 二维随机向量的协方差COV和相关系数ρ

5.1 协方差COV定义

5.2 协方差COV的性质 

5.3 相关系数ρ

---

1. 二维随机向量(X,Y)的数学期望EX, EY

离散形式 和 连续形式，求向量中的单个变量的期望：

 

2. 二维随机向量函数z=g(X,Y)的数学期望EZ

3. 二维随机向量(X,Y)的方差DX, DY

4. 二维随机向量的性质（和、积的数学期望E与方差D）

5. 二维随机向量的协方差COV和相关系数ρ

5.1 协方差COV定义

(有的地方用符号  表示协方差)

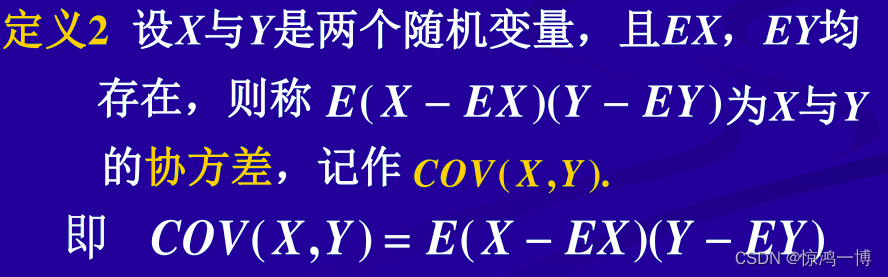
5.2 协方差COV的性质 

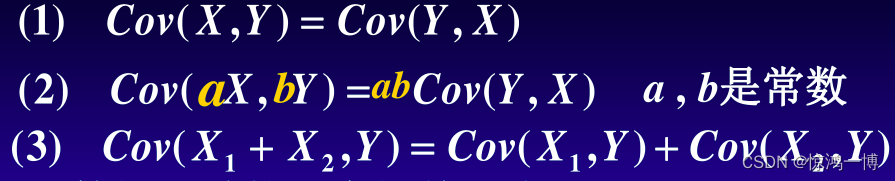
 求协方差的一个公式

可以看出 , 同一个变量的协方差等于该变量的方差

协方差COV 与 随机变量X,Y的相关性

协方差的符号是有意义的：

• 协方差为正，说明两变量同向变化；
• 协方差为负，二者反向变化；
• 协方差为0，说明二者变化不相关，即二者独立。

 

二元随机变量X,Y的方差D和协方差COV的关系

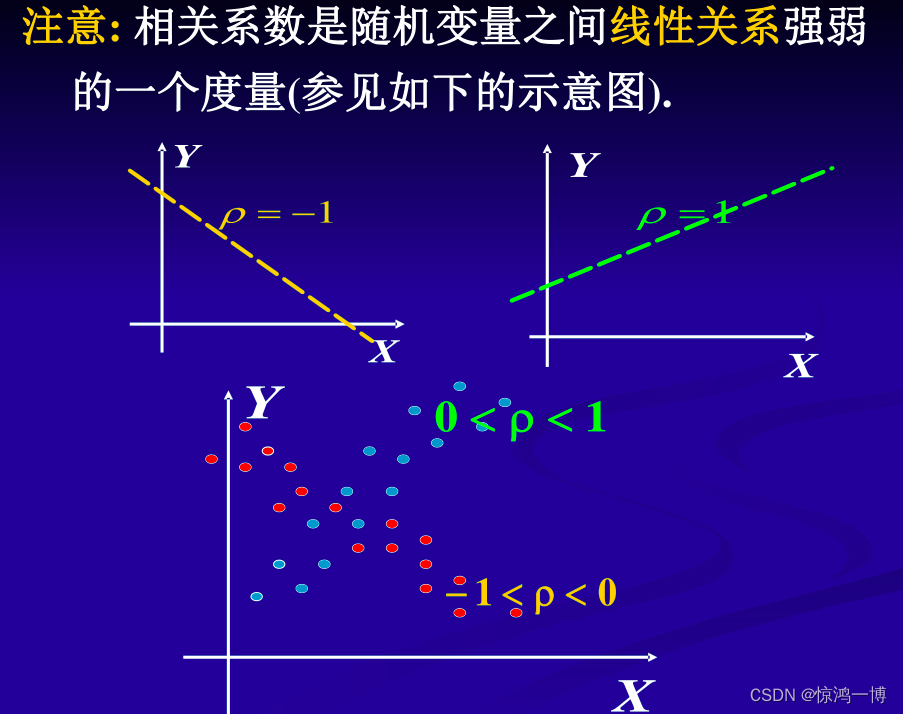
5.3 相关系数ρ

性质：相关系数的绝对值一定小于等于1，证明如下：

 

参考：

二元变量数学期望与方差 - 道客巴巴