图像变换是基于像素的映射,区别是像素是怎么映射的。灰度变换的话是通过点对点的映射,也就是变换后的像素点之和当前的像素点有关(gramma变换、对数变换等等),依次来进行对比度拉伸。而空间滤波变换后的像素点是和当前像素点以及当前像素点周围的点有关,也就是对图像每个像素点的领域进行映射
直方图均衡化
直方图均衡化,它能够产生一个直方图具有均匀分布的输出图像
直方图处理是针对于全局的像素点,将任意图像的像素点的分布变换为均匀分布的形式,来增强灰度动态范围偏小的反差以此增强图像的对比度
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('./img.png', 0) # 读取灰度图像
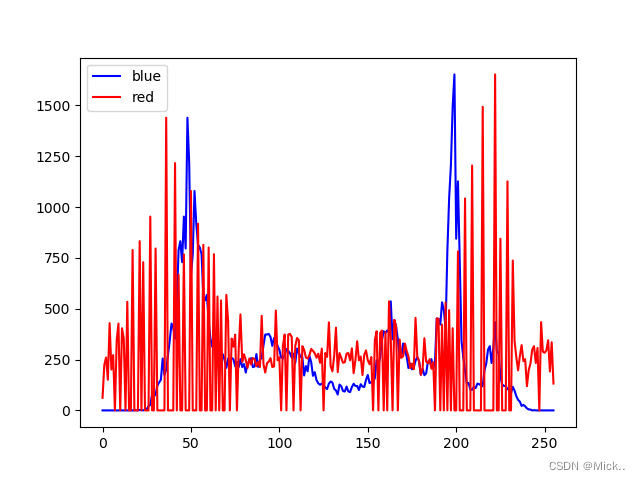
hist = cv2.calcHist([img], [0], None, [256], [0, 256]) # 原图的直方图
dst = cv2.equalizeHist(img) ##直方图均衡化
hist_dst = cv2.calcHist([dst], [0], None, [256], [0, 256]) # 均衡化之后的直方图
plt.plot(hist, color='b', label='blue')
plt.plot(hist_dst, color='r', label='red')
plt.legend() # 显示图例
plt.show()
cv2.imshow('img', np.hstack((img, dst)))
cv2.imwrite('./image.png',np.hstack((img, dst)))
cv2.waitKey()
cv2.destroyAllWindows()

直方图匹配
直方图匹配:用于生成规定直方图图像的方法
实现的原理也很简单,只需要将原图和目标图像分别均衡化,然后找对应图像的映射就可以
import cv2
import numpy as np
import matplotlib.pyplot as plt
def transforms(x, y): # x 是原图像 y 是目标图像
transform = np.zeros(256) # 建立一个映射表,形如[1 2 3 4],index代表原图像灰度值,value代表变化后的灰度值
for index in range(256):
gray_value = 0 # 更新映射表transform的值
value_min = np.fabs(x[index] - y[0]) # 从0开始建立映射表
for j in range(256):
diff = np.fabs(x[index] - y[j]) # 检索归一化累计直方图灰度值最近的点
if (diff < value_min):
gray_value = j # 和原图灰度值为i最接近的匹配灰度值为j
value_min = diff
transform[index] = gray_value # 更新映射表
img_out = transform[img].astype(np.uint8) # 图像映射
return img_out
img = cv2.imread('./img1.png', 0) # 原图
dst = cv2.imread('./img2.png', 0) # 目标图像
img_hist = cv2.calcHist([img], [0], None, [256], [0, 256]) # 计算原图的直方图
dst_hist = cv2.calcHist([dst], [0], None, [256], [0, 256]) # 计算匹配图像的直方图
img_hist_norm = cv2.normalize(img_hist, None, norm_type=cv2.NORM_L1) # 直方图归一化
dst_hist_norm = cv2.normalize(dst_hist, None, norm_type=cv2.NORM_L1) # 计算匹配图像的直方图归一化
img_hist_norm_accu = img_hist_norm.cumsum() # 归一化累计直方图
dst_hist_norm_accu = dst_hist_norm.cumsum() # 目标图像的归一化累计直方图
img_transforms = transforms(img_hist_norm_accu, dst_hist_norm_accu) # 直方图匹配
old_hist = cv2.calcHist([img], [0], None, [256], [0, 256])
dst_hist = cv2.calcHist([dst], [0], None, [256], [0, 256])
after_hist = cv2.calcHist([img_transforms], [0], None, [256], [0, 256])
plt.plot(old_hist, color='r', label='img') # 原图的直方图
plt.plot(dst_hist, color='g', label='dst') # 匹配图像的直方图
plt.plot(after_hist, color='b', label='img_transform') # 直方图匹配后的图像直方图
plt.legend()
plt.show()
cv2.imshow('img', np.hstack((img, img_transforms))) # 展示原图和直方图匹配后的图像
cv2.waitKey()
cv2.imwrite('./image.png',np.hstack((img, img_transforms)))
cv2.destroyAllWindows()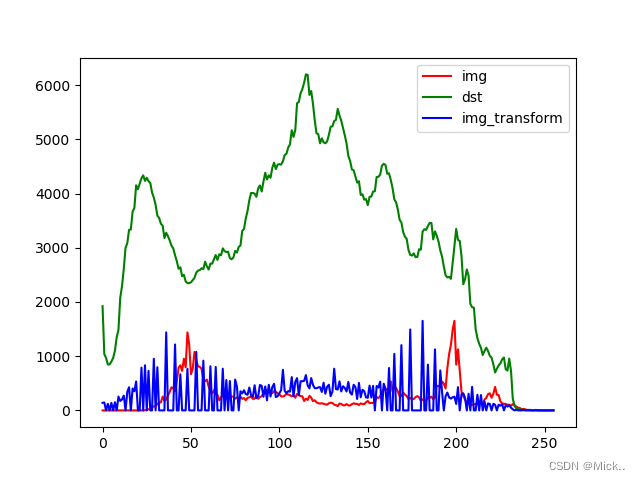

直方图局部处理
直方图均衡化或者直方图匹配化都是全局性的技术,因为像素都是基于整幅图像的灰度分布进行修改的。这种方法适合于整体的增强,但如果只是想增强图像几个小区域的时候,效果往往是不好的。原因是,在小区域的时候,像素数量对计算全局变换的影响可以忽略
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('./img1.png', 0)
img_HE = cv2.equalizeHist(img) # 直方图均衡化
clahe = cv2.createCLAHE(clipLimit=2, tileGridSize=(8, 8))
img_CLAHE = clahe.apply(img) # 应用CLAHE算法
img_hist = cv2.calcHist([img], [0], None, [256], [0, 256])
img_HE_hist = cv2.calcHist([img_HE], [0], None, [256], [0, 256])
img_CALME_hist = cv2.calcHist([img_CLAHE], [0], None, [256], [0, 256])
plt.plot(img_hist, color='r', label='img')
plt.plot(img_HE_hist, color='b', label='img_HE')
plt.plot(img_CALME_hist, color='g', label='img_CLAHE')
plt.legend()
plt.show()
cv2.imshow('img', np.hstack((img, img_HE, img_CLAHE)))
cv2.imwrite('./image.png',np.hstack((img, img_HE, img_CLAHE)))
cv2.waitKey()
cv2.destroyAllWindows()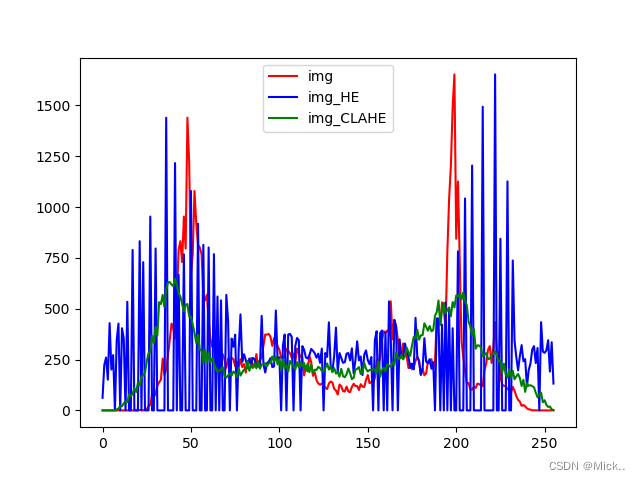

参考文献
空域变换-直方图均衡化(直方图修正)_Henry_zs的博客-CSDN博客