串基本概念：串是由零个或者多个字符组成的有限序列，一半记作S='a1,a2,a3,a4.......'（n>=0，串的长度）

1.S == 串的名字     n ==  串当中字符串的个数，称为串的长度。

串的常用术语

1.空串（null string）：长度为零的串，它不包含任何字符。

2.空格串(black string) :任由一个或多个空格组成的串，长度大于等于1

3.子串（sub string）:串中任意个连续字符的组成的子序列称为该串的“子串”

4.主串（master string):包含子串的串相应的称为“主串”，因此子串是主串的一部分。

5.前缀子串（prefix sub string）：S的前缀子串是一个子串U,记作U = 'a1,.....ab'(1<=b<=n)，当1<=b<n时，则相应的U称为S的“真前缀子串”。

6.后缀子串（suffix sub string）：S的后缀子串是一个子串U,记作U = 'an-b-1....an'(1<=b<=n)，当1<=b<n时，

eg.S='abccset',S的前缀子串是‘a’,'ab','abc','abcc','abccs','abccse'。S的后缀子串是‘t’,'et','set','cset','ccset','bccset'。

7.位置:通过将字符在串中的序号，称为该字符在串中的“位置”。子串在主串中的位置则以子串的第一个字符在主串中的位置来表示。

8.串相等：当且仅当两个串的值相等的时候，则称两个串的数值相等。条件：长度相等以及位置必须相等

9.模式匹配：确定子串在主串的某个位置开始后，在主串中首次出现的位置的运算。主串=="目标串"，子串==“格式串”。

eg. 串A = “abcaabsbcas”，串B = "bca",从第一个位置开始，匹配的运算结果是2，从第四个位置开始的运算结果是8。

串的基本运算

 1.strInsert(S,pos ,T)

设S='chater',T=‘rac’,运行StrInsert(S,4,T),S='character'

2.strDelete(S.pos,len)

设S='chapter',运行StrDelete(S,5,3),则S='chap'

3.StrCat(S,T)

设串S='man',运行Strcat(S,'kind'),则S='mankind'

4.Substring(T,S,pos,len)

eg.设串S='commander',运行SubString(Sub1,S,4,3),则Sub1='man'。

5.StrIndex(S,pos,T)

设S='abcaabcaaabc',T='bca',运行StrIndex(S,1,T),返回2，运行StrIndex(S,4,T)，返回值是 6。

6.StrReplace(S,T,V)

eg.设S='abcaabcaaabca',T='bca',若V='x',则S='axaxaax',若V='bc',则S='abcancaabc'

串的存储结构以及实现

 定义顺序串

1.定长顺序串存储结构

#define MAXSIZE 50
typedef struct
{
	char ch[MAXSIZE+1];       //0号元素不使用（浪费一个空间），每个分量存储一个字符。
	int len;
}SString;

 串的实际长度可以在MAXSIZE范围内随意变动，超过范围的会舍去，称为“截断”。

2.定长串的基本操作实现

插入：三种情况

int SStrInsert(SString *S,int pos,const SSttring T)
{
	int i;
	if(pos<1 || pos >S->len+1)
	return 0;
	//插入的子串没有超过最大值且主串不需要舍弃 
	if(S->len + T.len<=MAXSIZE)
	{
		for(i = S->len+T.len;i>=pos+T.len;i--)
		{
		 	S->ch[i] = S->ch[i-T.len];
		}
		for(i = pos;i<S->len+T.len;i++)
		{
			S->ch[i] = S->ch[i-pos+1]
		}
		S->len = S->len + T.len;
	}
	//子串可以完全插入，但是主串需要舍弃一部分 
	else if(pos+T.len<=MAXSIZE)
	{
		for(i = MAXSIZE;i>=pos+T.len;i--)
		{
			S->ch[i] = S->ch[i-T.len]
		}
		for(i = pos;i<S->len+T.len;i++)
		{
			S->ch[i] = S->ch[i-pos+1]
		}
		S->len = MAXSIZE;
	 } 
	//子串插入在任意位置，都超出了最大范围 
	else
	{
		for(i = pos ;i<=MAXSIZE;i++)
		{
			S->ch[i] = T.ch[i-pos+1]
		}
		S->len = MAXSIZE;
	}
	return 1;
}

删除函数：

int SStrDelete(SSting *S,int pos,int len)
{
	int i = 1;
	if(pos<1 || pos>S->len || len<0 || len>S->len-pos+1)
	{
		return 0;
	}
	for(i = pos;i<S->len-len;i++)
	{
		s->ch[i] =  S->ch[i+len]; 
	}
	return 1;
} 

串的连接

1.连接后串长小于等于MaxSize,则直接连接在第一个串的后面。

2.连接后，当串长大于MaxSize,且原始串的长度小于MaxSize，则待连接串则会舍弃一部分，当原始串长==MaxSize，则将待连接串全部进行舍弃。

int SStrCat(SSting *S,const SString T)
{
	int i = 1;
	if(S->len+T.len<=MaxSize)
	{
		for(i = S->len;i<=S->len+T.len;i++)
		{
			S->ch[i] = S.ch[i-S->len];
		}
		S->len = S->len+T.len;
	}
	else if(S->len<MaxSize)
	{
		for(i=S->len;i<=MaxSize;i++)
		{
			S->ch[i] = S->ch[i-S->len]	
		}	
		S->len = MaxSize;
	}
	else
	return 0;
}

堆串（相较于定长的顺序串，堆串可以动态的分配内存空间，这样可以保证不会出现截断的情况）

1.串的初始化 

void HSrInit(HString *S)
{
	S->ch = NULL;
	S->len = 0;
}HString;

2.串的赋值操作

int HstrAssign(HString  *S,const char * chars)
{
	int i = 0;
	while(char[i] != '\0')
	i++;
	S->len = i;
	if(0 != S->len)
	{
		if(S->ch != NULL)
		free(S->ch);
		S->ch = (char *)malloc((S->len + 1) * sizeof(char));
		if(NULL == S->ch)
		return 0;
		for(i = 1;i<=S->len;i++)
		{
			S->ch[i] = chars[i-1];
		}
	else
	S->ch = NULL;
	return 1;
	}	
} 

3.串的插入

int HStrInsert(HString *S,int pos,const HString T)
{
	int i;
	char * temp;
	if(pos>S->len || pos<1)
	return 0;
	temp = (char *)malloc(sizeof(S->len+T.len + 1)*sizeof(char));
	if(temp == NULL)
	return 0;
	for(i = 0;i<pos;i++)
	temp[i] = S->ch[i];
	for(i = pos;i<pos+T.len;i++)
	temp[i] = S->ch[i-pos+1];
	for(i = pos+T.len;i<=S->len+T.len;i++)
	temp[i] = S->ch[i-T.len];
	free(S->ch)
	S->ch = temp;
	S->len+=T.len;
	return 1; 
}

4.串的删除

int HStrDelete(HString *S,int pos,int len)
{
	int i;
	char *temp;
	if(len<0 || pos<1 || pos>S->len-len+1)
	return 0;
	temp = (char *)malloc(sizeof(S->len-len+1) * sizeof(char));
	if(NULL == temp)
	return 0;
	for(i = 0;i<pos;i++)
	temp[i] = S->ch[i];
	for(i = pos;i<=S->len-len;i++)
	temp[i] = S->ch[i+len];
	free(S->ch);
	S->ch = temp;
	S->len-=len;
	return 1;
}

5.串的连接

int HStrCat(HString * S,const HString)
{
	int i = 1;
	S->ch = (char *)malloc(S->ch,(S->len +T.len +1)*sizeof(char));
	if(NULL == S->ch)
	return 0;
	for(i = S->len+1;i<=T.len+S->len;i++)
	S->ch[i] = T.ch[i-S->len];
	S->len = S->len + T.len;
	return 1;
}

块链串（链表的每一个结点存放一个字符或者多个字符，每个结点称为块，整个链表称为“块链结构”）

 块大小：块链表存放字符的个数

当块的大小 == 1的时候，增删改查的方法和单链表一样，因为只有一个数据域和一个指针域，但当块的大小 ≠ 1的时候，则需要进行结点的拆分和合并....

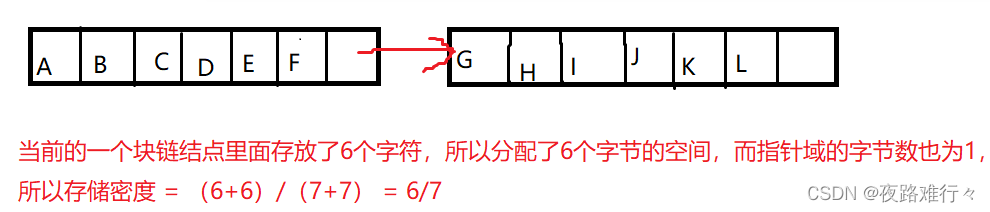
存储密度：存储密度 = 串值所占的存储位 / 实际分配的存储位

串的模式匹配

1.BF模式匹配算法 

思路：从主串的第一个字符开始进行匹配，当主串和子串的字符不相同的时候，就回溯到开始字符的下一个字符，重新开始进行匹配，知道找到为止

int indedx(SString S,int pos,SString T)
{
	int i = pos,j = 1;
	while(i<=S.len && j<=T.len)
	{
		if(S.ch[i] == T.ch[j])
		i++,j++;
		else
		{
			i = i-j+2;    //返回到起始比较字符的下一位，重新开始判断
			j = 1;
		}
	}
	if(j > T.len)
	return i-T.len;
	else
	return 0;
}

2.KMP模式匹配算法

思路：相对于暴力索引求解，KMP的时间复杂度大大降低，开始都是和BF算法一样，一个一个字符进行匹配，但当主串和子串的字符不相等的时候，不再是回到主串中开始比较字符的下一位，而是进行一个“子串向后移动最长前后缀相等子串长度”，最后找到对应的字符串。（详细介绍：数据结构KMP算法配图详解（超详细）_哈顿之光的博客-CSDN博客_kmp算法难吗是什么级别）

这里需要好好理解一下next数组的作用（记录当前字符的前面的最长前后缀相等的字符串）

首先将模式串的每一个字符对应的next的数值求出来

eg. "ABCABCKO"

 这样就得到了当前每一个字符对应的next数组的数值。

void Get_Next(SString T,int next[])
{
	int j = 1,k = 0;
	next[1] = 0;
	while(j < T.len)
	{
		if(k == 0 || T.ch[j] == T.ch[k])
		{
			++j;
			++k;
			next[j] = k;
		}
		else
		k = next[k];
		printf("%d \n",next[k]);
	}
}

int KMPIndex(SqString s,SqString t)  //KMP
{

	int next[MaxSize],i=0,j=0;
	GetNext(t,next);
	while (i<s.length && j<t.length) 
	{
		if (j==-1 || s.data[i]==t.data[j]) 
		{
			i++;j++;  			//i,j各增1
		}
		else j=next[j]; 		
    }
    if (j>=t.length)
		return(i-t.length);  	
    else  
		return(-1);        		
}