图-多叉树的直径（hard）

news2025/11/4 8:59:01

一、问题描述

二、解题思路

1.存储结构

2.算法描述

三、代码实现

四、刷题链接

五、参考

一、问题描述

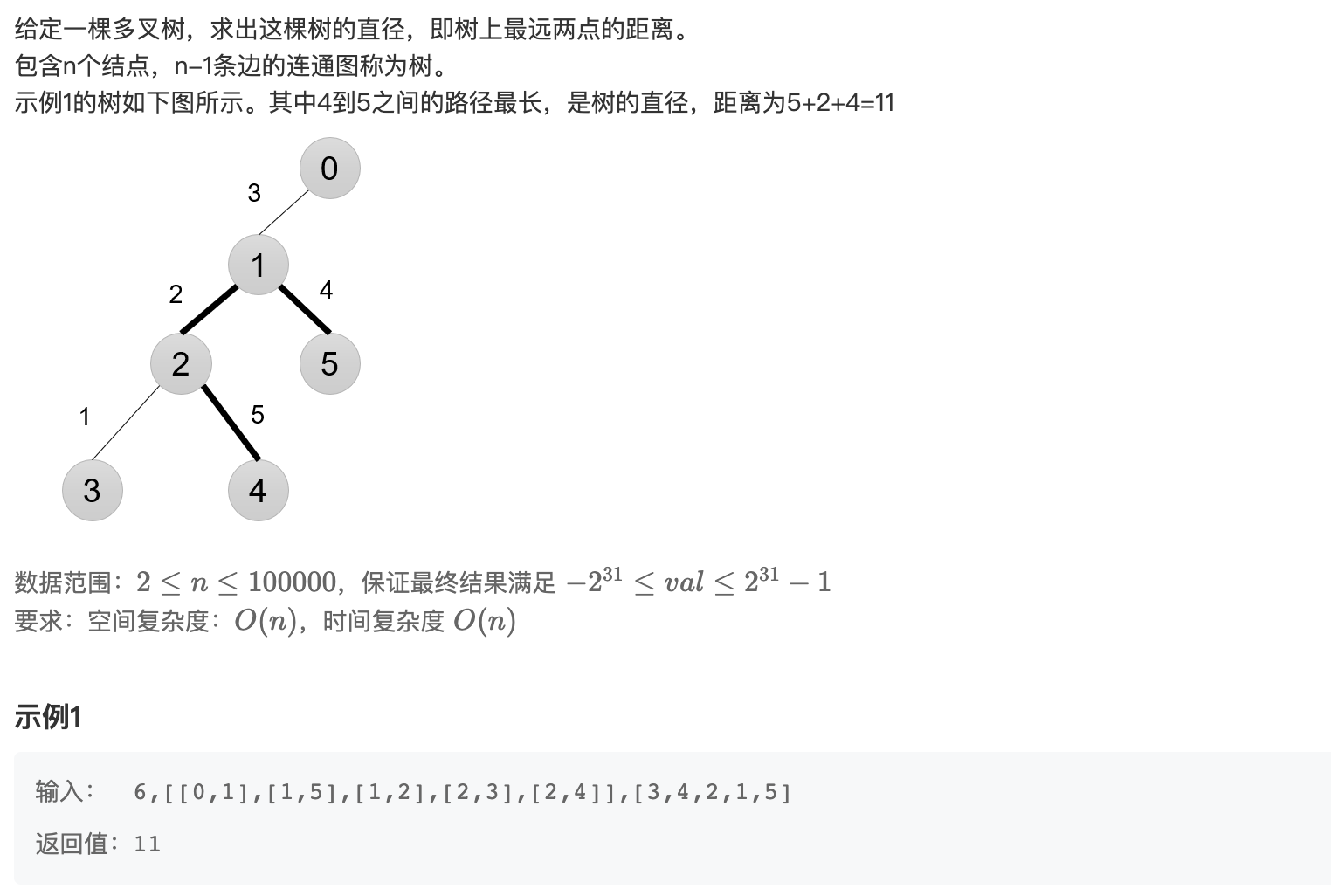
二、解题思路

1.存储结构

使用邻接表结构来存储无向图，边结点存储结构为[终点，边长(也就是权重)]

2.算法描述

从某一个结点（任意一个即可）开始进入递归，通过递归找到当前结点所能到达的最远结点（路径长度最长）。

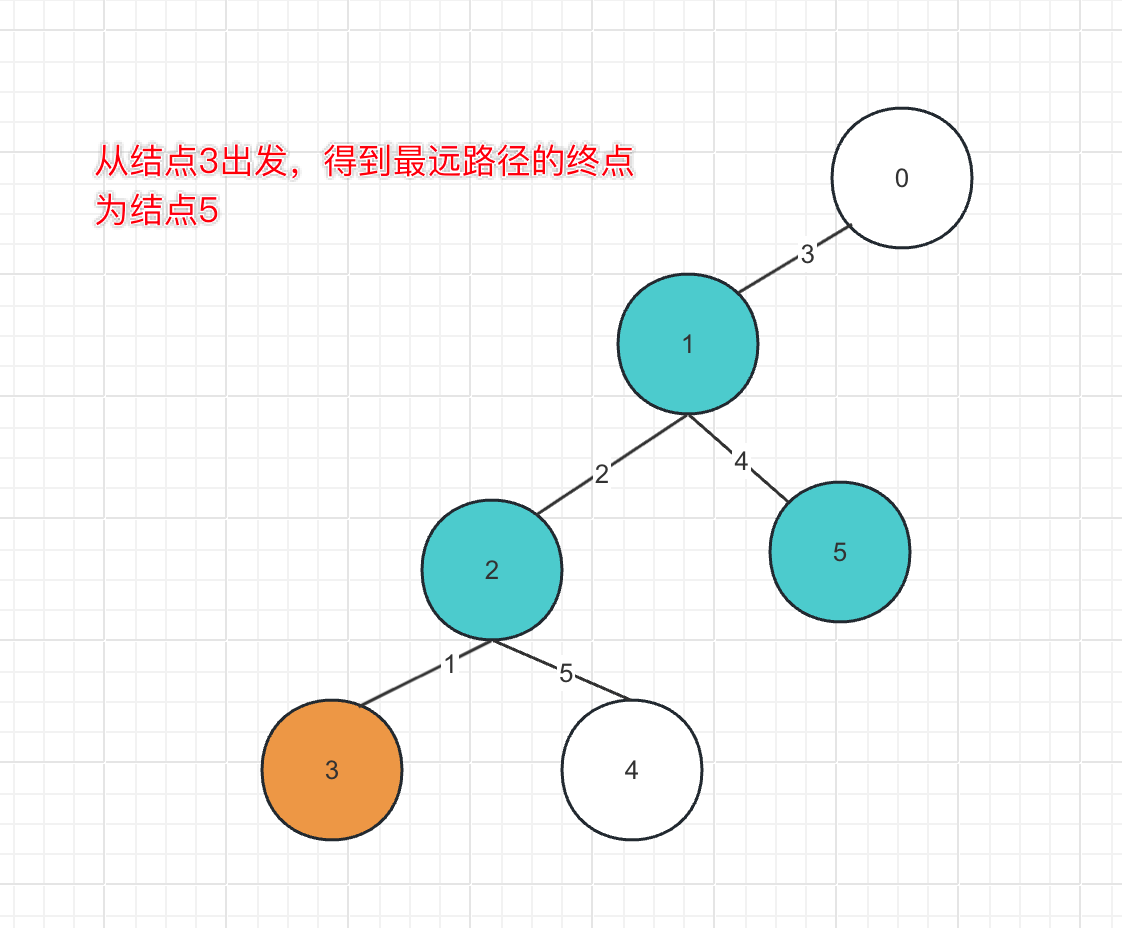
然后再从确定的最远结点开始进入递归，寻找距离这个最远结点最远的结点，这两个结点之间的距离就是最大的路径权值和，也就是题意里面要求的半径长度。

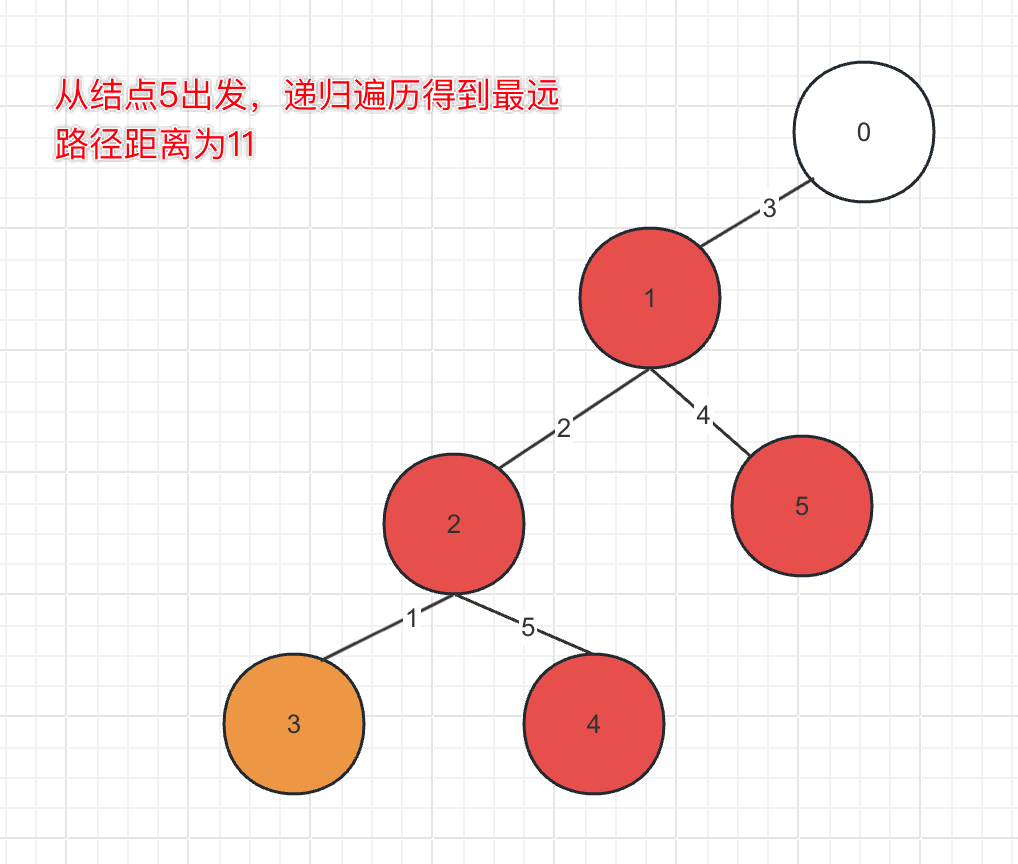
三、代码实现

import java.util.*;

/*
 * public class Interval {
 *   int start;
 *   int end;
 * }
 */

public class Solution {
    /**
     * 树的直径
     * @param n int整型 树的节点个数
     * @param Tree_edge Interval类一维数组 树的边
     * @param Edge_value int整型一维数组 边的权值
     * @return int整型
     */
    //邻接表
    List<List<int[]>> graph;
    //记录最远节点
    long far = 0;
    //记录无重复最长路径，即树的直径
    long max = 0;

    public int solve (int n, Interval[] Tree_edge, int[] Edge_value) {
        //初始化邻接表
        graph = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            graph.add(new ArrayList<>());
        }

        //以边的起点为索引，将对应的边的终点以及边的权值放在list里
        for (int i = 0; i < Tree_edge.length; i++) {
            graph.get(Tree_edge[i].start).add(new int[] {Tree_edge[i].end, Edge_value[i]});
            graph.get(Tree_edge[i].end).add(new int[] {Tree_edge[i].start, Edge_value[i]});
        }

        //从0号节点开始递归
        dfs(0, -1, 0);
        max = 0;
        //找到最远点后，从当前点递归
        dfs(far, -1, 0);
        return (int)max;
    }

    //深度优先搜索
    private void dfs(long cur, long pre, long dist) {
        //跟新当前最长路径以及最远点
        if (dist > max) {
            max = dist;
            far = cur;
        }
        for (int[] child : graph.get((int)cur)) {
            //如果没有走回头路，则沿子节点方向递归
            if (child[0] != (int)pre) {
                dfs(child[0], cur, dist + child[1]);
            }
        }
    }
}