目录
- 1.算法原理
- 2.改进点
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.算法原理
【智能算法】灰狼算法(GWO)原理及实现
2.改进点
混沌反向学习策略
融合Logistic混沌映射和Tent混沌映射生成Logistic-Tent复合混沌映射:
Z
i
+
1
=
{
(
r
Z
i
(
1
−
Z
i
)
+
(
4
−
r
)
Z
i
/
2
)
m
o
d
1
,
Z
i
<
0.5
(
r
Z
i
(
1
−
Z
i
)
+
(
4
−
r
)
(
1
−
Z
i
)
/
2
)
m
o
d
1
,
Z
i
⩾
0.5
(1)
Z_{i+1}=\begin{cases}(rZ_i(1-Z_i)+(4-r)Z_i/2) \mathrm{mod}1,Z_i<0.5\\(rZ_i(1-Z_i)+(4-r)(1-Z_i)/2) \mathrm{mod}1,Z_i\geqslant0.5\end{cases}\tag{1}
Zi+1={(rZi(1−Zi)+(4−r)Zi/2)mod1,Zi<0.5(rZi(1−Zi)+(4−r)(1−Zi)/2)mod1,Zi⩾0.5(1)
为了加快种群收敛速度,采用精英反向学习策略使得生成的初始种群偏向全局最优解:
X
n
∗
=
r
a
n
d
∗
(
u
b
+
l
b
)
−
X
n
(2)
X_n^*=rand*(ub+lb)-X_n\tag{2}
Xn∗=rand∗(ub+lb)−Xn(2)
控制参数调整
引入Sigmoid函数,修改收敛因子a,论文采用a1:
a
1
(
i
)
=
a
initial
−
a
initial
−
a
final
1
+
e
−
10
(
i
I
max
−
1
2
)
a
2
(
i
)
=
2
−
2
i
I
max
a
3
(
i
)
=
a
initial
−
a
initial
1
e
−
1
(
e
i
I
max
−
1
)
a
4
(
i
)
=
2
−
2
sin
(
λ
i
I
max
π
+
ϕ
)
(3)
\begin{aligned}a_1\left(i\right)=&a_\text{ initial}-\frac{a_\text{ initial}-a_\text{ final}}{1+e^{-10(\frac i{I_{\max}}-\frac12)}}\\a_2\left(i\right)=&2-\frac{2i}{I_{\max}}\\a_3\left(i\right)=&a_\text{ initial}-a_\text{ initial}\frac1{e-1}(e^{\frac i{I_{\max}}}-1)\\a_4\left(i\right)=&2-2\sin(\lambda \frac i{I_{\max}}\pi+\phi )\end{aligned}\tag{3}
a1(i)=a2(i)=a3(i)=a4(i)=a initial−1+e−10(Imaxi−21)a initial−a final2−Imax2ia initial−a initiale−11(eImaxi−1)2−2sin(λImaxiπ+ϕ)(3)
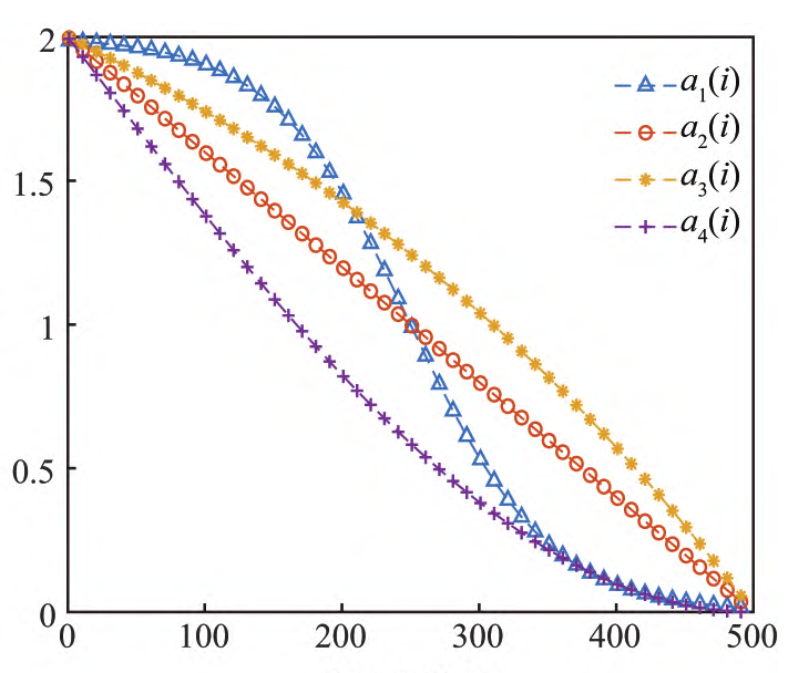
控制参数C1取值影响算法的寻优能力,当C1>1算法具有较强的局部开发能力;当C1<=1有利于增强算法全局探索能力:
C
1
(
i
)
=
2
η
−
a
1
(
i
)
(4)
C_1(i)=2\eta-a_1(i)\tag{4}
C1(i)=2η−a1(i)(4)
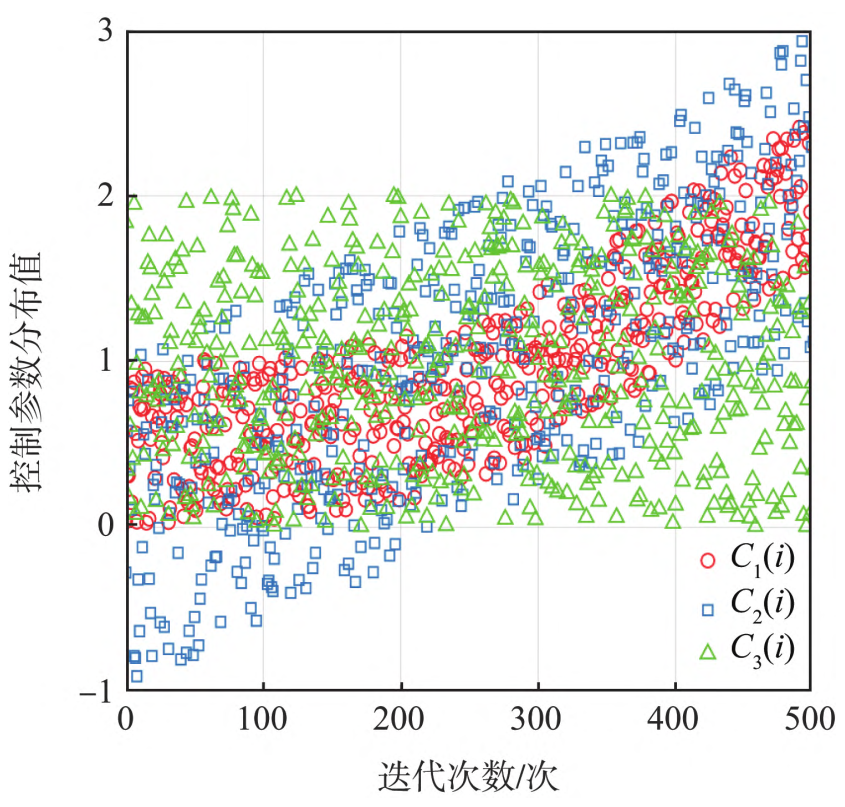
位置更新与种群淘汰策略
采用基于适应度值的比例权重更新灰狼位置:
X
(
i
+
1
)
=
∑
j
=
α
,
β
,
δ
ω
j
X
j
(
i
)
(5)
X\left(i+1\right)=\sum_{j=\alpha,\beta,\delta}\omega_jX_j\left(i\right)\tag{5}
X(i+1)=j=α,β,δ∑ωjXj(i)(5)
权重系数表述为:
w
j
=
f
i
t
(
X
j
(
i
)
)
f
i
t
(
X
α
(
i
)
)
+
f
i
t
(
X
β
(
i
)
)
+
f
i
t
(
X
δ
(
i
)
)
(6)
w_j=\frac{\mathrm{fit}(X_j(i))}{\mathrm{fit}(X_\alpha(i))+\mathrm{fit}(X_\beta(i))+\mathrm{fit}(X_\delta(i))}\tag{6}
wj=fit(Xα(i))+fit(Xβ(i))+fit(Xδ(i))fit(Xj(i))(6)
每次迭代后选择适应度最差的G匹狼进行淘汰,通过Logistic-Tent复合混沌映射生成新的狼以替代被淘汰的狼。种群淘汰机制可以剔除适应度最差的狼,但是无法保证生成的新狼适应度值一定优于原来的解。因此将种群淘汰机制与贪心策略相结合贪心策略使用适者生存的原则,使得新生成狼的适应度值必定优于原来的适应度值$:
M
i
+
1
=
M
i
′
,
f
i
t
(
M
i
′
)
<
f
i
t
(
M
i
)
(7)
M_{i+1}=M^{\prime}_i,\mathrm{fit}(M^{\prime}_i)<\mathrm{fit}(M_i)\tag{7}
Mi+1=Mi′,fit(Mi′)<fit(Mi)(7)
3.结果展示
CEC2005
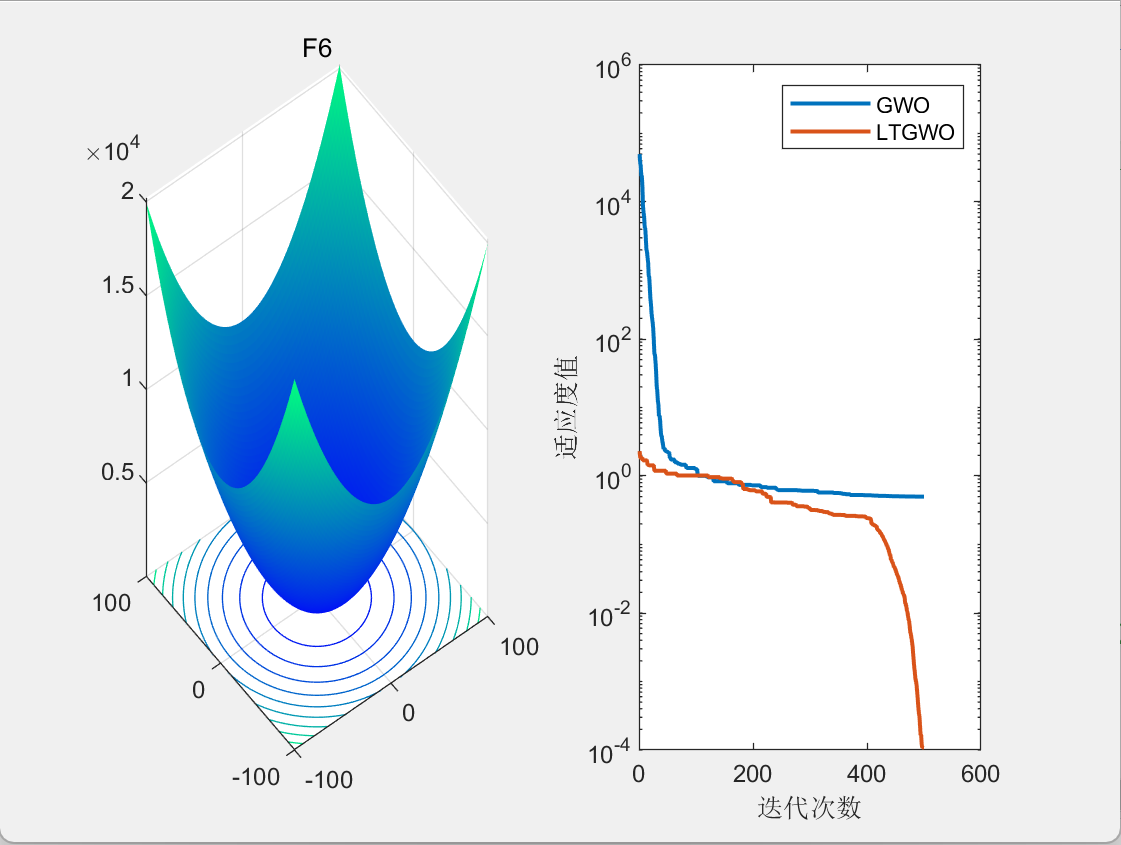
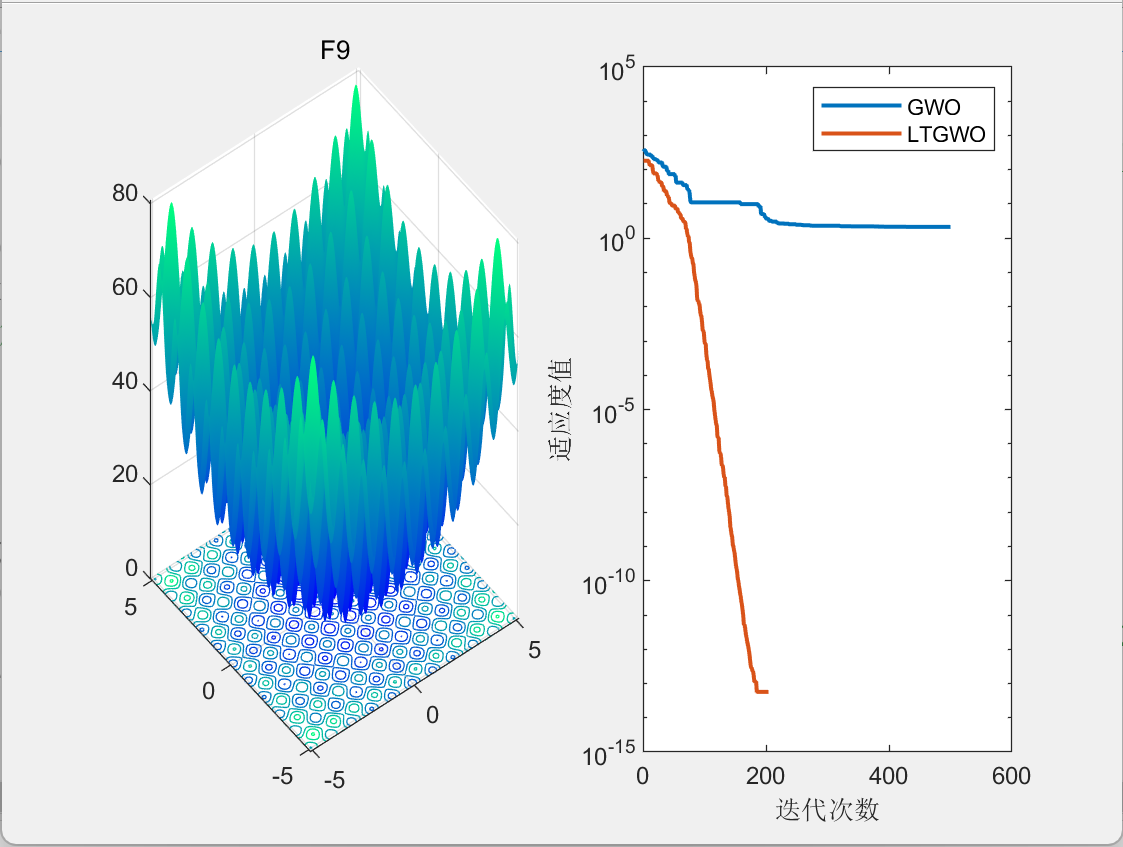
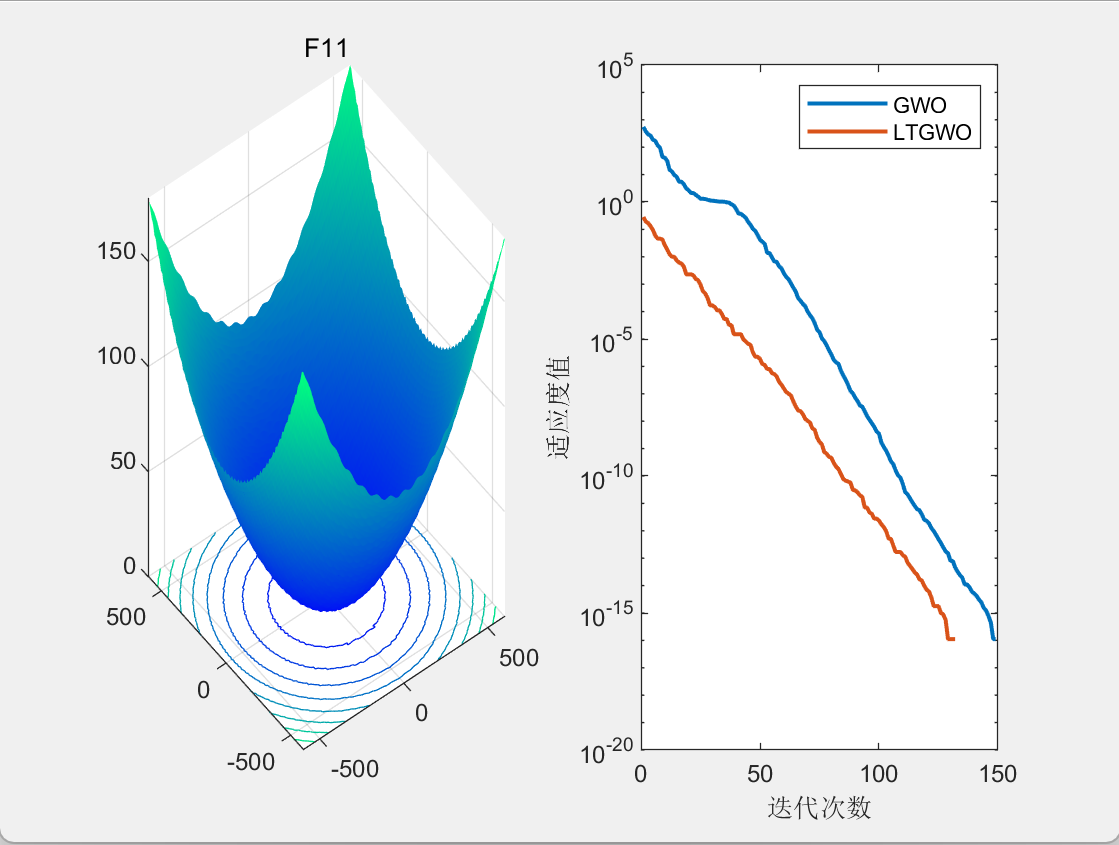
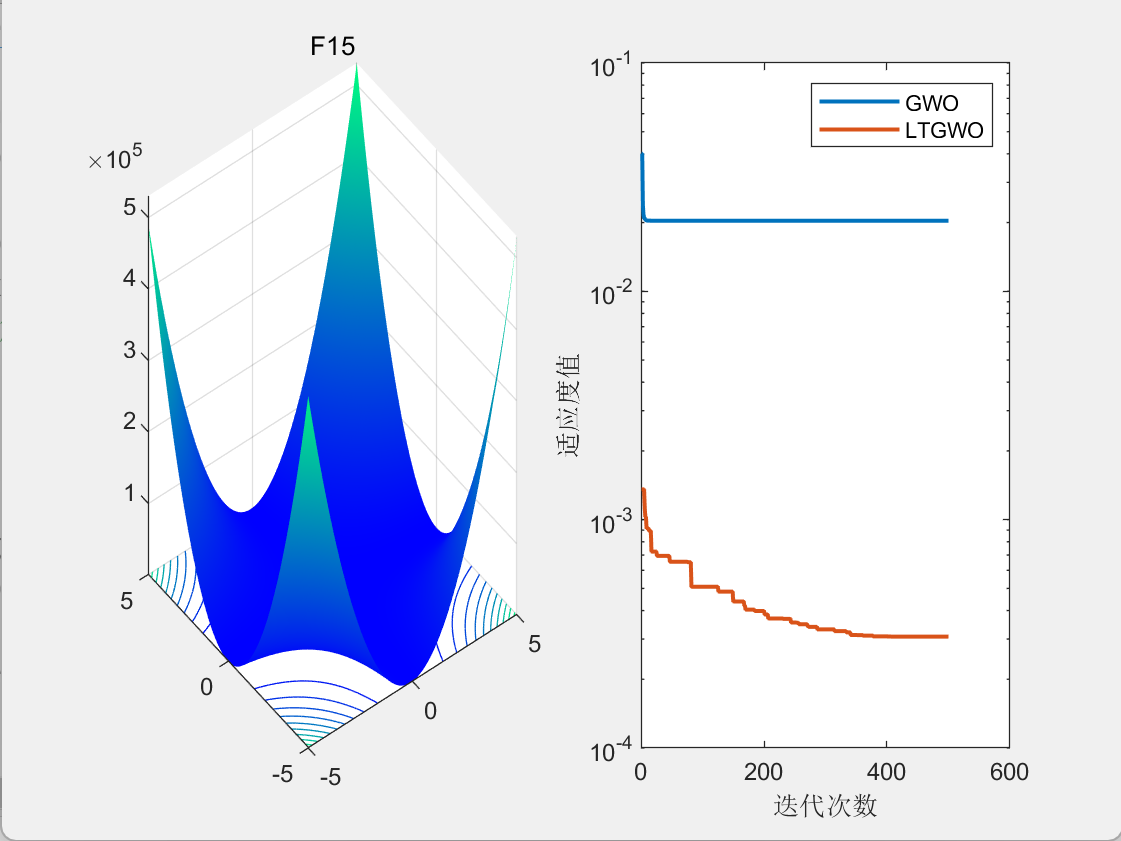
二维栅格路径规划
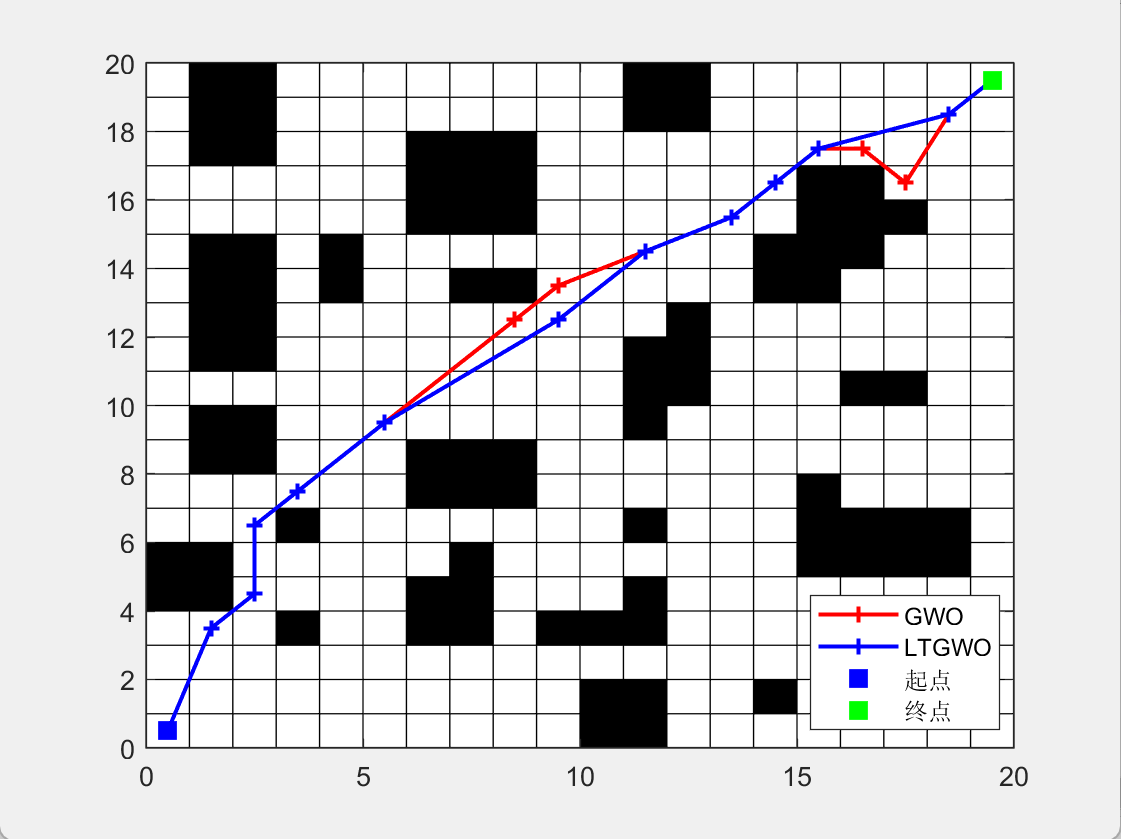
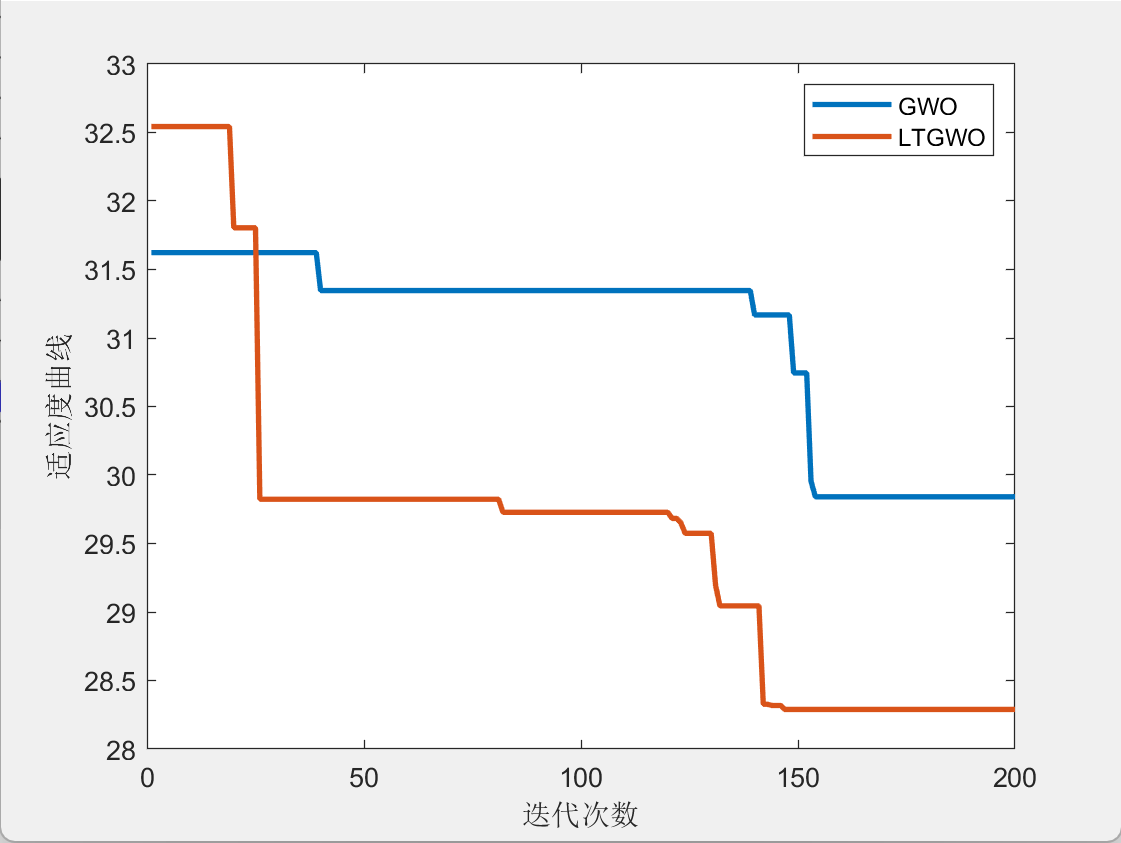
4.参考文献
[1] 黄琦,陈海洋,刘妍,等.基于多策略融合灰狼算法的移动机器人路径规划[J].空军工程大学学报,2024,25(03):112-120.