【因果推断python】33

【因果推断python】33_合成控制3

news2025/6/26 8:03:34

不要外推

假设您有下表中的数据，并被要求构建一个合成控制，以使用控制单元的任何线性组合来重现处理过的单元。

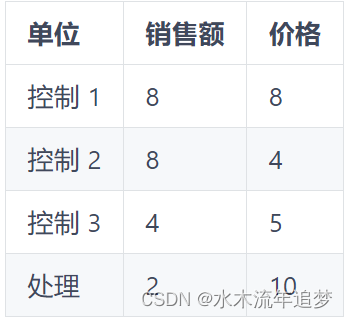
由于有 3 个单位和只有 2 个属性要匹配，因此有多个确定性的解决方案可以解决这个问题，但一个不错的解决方案是将第一个控件乘以 2.25，将第二个控件乘以 -2，然后将两者相加。请注意第二次乘法如何创建一个销售量为 -16 且价格为 -8 的假单位。这种乘法将控制 2 单元外推到没有多大意义的数据区域，因为负价格和销售几乎是不可能的。第一个乘法也是外推，因为它将第一个单位带到销售和价格为 18 的地区。这些数字远高于我们数据中的任何数字，因此是外推。

当我们要求它创建合成控制时，这就是回归正在做的事情。外推在技术上并没有错，但在实践中却很危险。我们假设我们从未见过的数据表现得像我们拥有的数据。

一种更安全的方法是将我们的合成控制限制为仅进行插值。为此，我们将权重限制为正且总和为 1。现在，合成控制将是供体池中单元的凸组合。在进行插值时，我们会将处理后的单元投影到由未处理单元定义的凸包中.

这里注意两点。首先，在这种情况下，插值将无法创建处理单元的完美匹配。这是因为被处理的是销量最少、价格最高的单位。凸组合只能精确复制控制单元之间的特征。另一件需要注意的是插值是稀疏的。我们将处理过的单元投影到凸包的墙上，而这面墙仅由几个单元定义。出于这个原因，插值将为许多单元分配零权重。

这是一般的想法，现在让我们将其形式化一点。合成控制仍定义为

$\hat{Y}^N_{jt} = \sum^{J+1}{j=2} w_j Y{jt}$

但是现在，我们将使用最小化的权重 $\boldsymbol{W}=(w_2,\ldots,w_{J+1})$

$||\pmb{X}1 - \pmb{X}0 \pmb{W}|| = \bigg(\sum^k{h=1}v_h \bigg(X{h1} - \sum^{J+1}{j=2} w_j X{hj} \bigg)^2 \bigg)^ {\frac{1}{2}}$

受限于 $w_2,\ldots,w_{J+1}$ 为正且总和为 1。请注意， $v_{h}$ 在最小化处理和合成控制之间的差异时反映了每个变量的重要性。不同的 vs 会给出不同的最佳权重。选择 V 的一种方法是使每个变量都具有均值零和单位方差。一种更复杂的方法是选择 V 以使有助于更好地预测 Y 的变量获得更高的重要性。由于我们希望保持代码简单，我们将简单地为每个变量赋予相同的重要性。

为了实现这一点，首先，定义上述损失函数。

from typing import List
from operator import add
from toolz import reduce, partial

def loss_w(W, X, y) -> float:
    return np.sqrt(np.mean((y - X.dot(W))**2))

由于我们对每个特征都使用相同的重要性，所以我们不需要担心 v。

现在，为了获得最佳权重，我们将使用 scipy 的二次规划优化。我们将限制权重总和为 1

lambda x: np.sum(x) - 1
此外，我们将优化界限设置在 0 和 1 之间。

from scipy.optimize import fmin_slsqp

def get_w(X, y):
    
    w_start = [1/X.shape[1]]*X.shape[1]

    weights = fmin_slsqp(partial(loss_w, X=X, y=y),
                         np.array(w_start),
                         f_eqcons=lambda x: np.sum(x) - 1,
                         bounds=[(0.0, 1.0)]*len(w_start),
                         disp=False)
    return weights
有了这个实现，让我们得到定义合成控制的权重

calif_weights = get_w(X, y)
print("Sum:", calif_weights.sum())
np.round(calif_weights, 4)
Sum: 1.0000000000007458
array([0.    , 0.    , 0.    , 0.0852, 0.    , 0.    , 0.    , 0.    ,
       0.    , 0.    , 0.    , 0.    , 0.    , 0.    , 0.    , 0.    ,
       0.    , 0.    , 0.    , 0.113 , 0.1051, 0.4566, 0.    , 0.    ,
       0.    , 0.    , 0.    , 0.    , 0.    , 0.    , 0.    , 0.    ,
       0.2401, 0.    , 0.    , 0.    , 0.    , 0.    ])

有了这个权重，我们将状态 1,2 和 3 乘以零，状态 4 乘以 0.0852 和很快。请注意权重是如何稀疏的，正如我们所预测的那样。此外，所有权重总和为 1，并且介于 0 和 1 之间，满足我们的凸组合约束。

现在，为了获得合成控制，我们可以将这些权重乘以状态，就像我们之前使用回归权重所做的那样。

calif_synth = cigar.query("~california").pivot(index='year', columns="state")["cigsale"].values.dot(calif_weights)

如果我们现在绘制合成控制的结果，我们会得到一个更平滑的趋势。另请注意，在干预前期间，合成对照不再精确复制处理过的对象。这是一个好兆头，因为它表明我们没有过度拟合。

plt.figure(figsize=(10,6))
plt.plot(cigar.query("california")["year"], cigar.query("california")["cigsale"], label="California")
plt.plot(cigar.query("california")["year"], calif_synth, label="Synthetic Control")
plt.vlines(x=1988, ymin=40, ymax=140, linestyle=":", lw=2, label="Proposition 99")
plt.ylabel("Per-capita cigarette sales (in packs)")
plt.legend();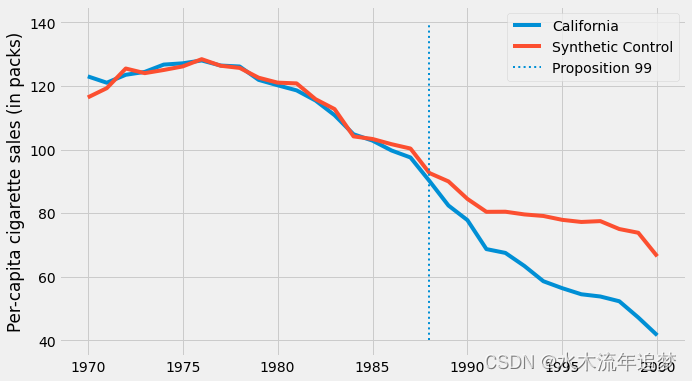

有了手头的合成控制，我们可以将干预效果估计为干预结果与合成控制结果之间的差距。

$\tau_{1t}=Y_{jt}^I-Y_{jt}^N$

在我们的具体案例中，随着时间的推移，效果会越来越大。

plt.figure(figsize=(10,6))
plt.plot(cigar.query("california")["year"], cigar.query("california")["cigsale"] - calif_synth,
         label="California Effect")
plt.vlines(x=1988, ymin=-30, ymax=7, linestyle=":", lw=2, label="Proposition 99")
plt.hlines(y=0, xmin=1970, xmax=2000, lw=2)
plt.title("State - Synthetic Across Time")
plt.ylabel("Gap in per-capita cigarette sales (in packs)")
plt.legend();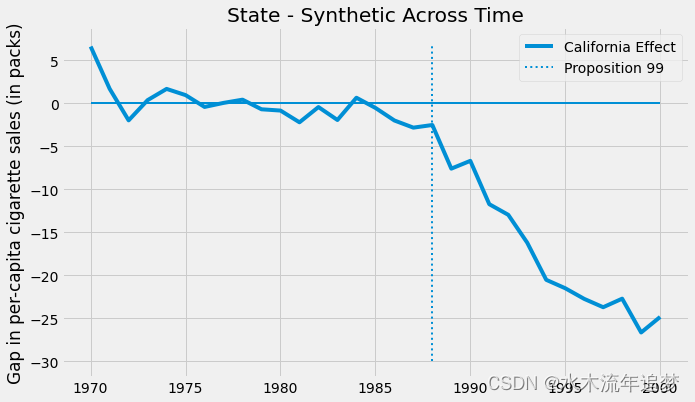

到 2000 年，99 号提案似乎将卷烟销量减少了 25 包。这很酷，但你可能会问自己：我怎么知道这在统计上是否显着？