文章目录
- 自变量
- 有理化
- 奇偶性
- 周期性
- 初等函数
自变量
自变量是x,这个还挺奇怪,记住就好
y
=
f
(
e
x
+
1
)
y=f(e^x+1)
y=f(ex+1) 里面
e
x
e^x
ex 只算中间变量,自变量是x
做这些题,想到了以前高中的时候做数学题,不够扎实呀,要是足够扎实,绝对不是95分的分数,应该多少也能考个110分(2022年新高考一卷的数学比较难),只能往前看了,现在学知识或者干啥整的扎实一些,我现在回想以前的高中知识,其实不在于刷多少题目,我买了很多刷题的书,其实很多都没写过几个题,白白浪费了,利用好已有的资料,把每一个细节自己慢慢想清楚,应该是对我来说最好的
需要判断一个函数的奇偶性,首先要看定义域是否关于原点对称,虽然感觉考试的时候一般都是对称的
一个分式和零的大小关系,可以转换成乘式和零的大小关系,这个应该是比较自然而然的
老师说一个简单的知识点记不住没办法,以前一个初中英语老师说她记英语单词就一个办法,死记,重复,其实是这样的,用的多了其实怎么都能记住了,有时候说自己记不住只是找个借口罢了,还是用的不够多,比如说你好,这两个汉字,用的非常多,哪怕一个人很久不写字也不至于不会写这两字吧
有理化
看到一个带根号的式子,根号且有加或者减去一个东西,可以考虑分式上下同时乘以一个元素,就是用平方差公式进行分子有理化
奇偶性
双曲正弦,双曲余弦,反双曲正弦,这几个函数都比较常见,但是在电脑上打数学公式比较麻烦,等之后我摸索出来怎么方便的在电脑上打出这些数学公式,我就把这些公式打上来,貌似也是有一些语法,其实我之前写算法题的时候也打过一些,但是现在好久没写算法题了,也差不多忘光了
算了不等以后,就现在就开始用latex打数学公式
F
(
x
)
=
f
(
x
)
+
f
(
−
x
)
2
偶函数
F(x)=\frac{f(x)+f(-x)}{2} \ \ 偶函数
F(x)=2f(x)+f(−x) 偶函数
F
(
x
)
=
f
(
x
)
−
f
(
−
x
)
2
奇函数
F(x)=\frac{f(x)-f(-x)}{2} \ \ 奇函数
F(x)=2f(x)−f(−x) 奇函数
上面两个公式记住,在判断奇函数偶函数的时候可能可以更加快速,因为给定的一个复杂函数可能可以拆开变成上面的形式
奇函数和偶函数相乘,或者就是排列组合,乘积得到的函数的奇偶性是什么,其实非常简单,把奇函数看成-1,偶函数看成1就好,之前看到这种结论还以为什么怪力乱神,其实想清楚之后挺简单
看网课,一下子就是两个小时,数据库也是,一看就是很长的时间,没一点儿战略耐心还真受不了
看完这个网课就去看数据库网课
周期性
哈哈有意思,做数学题用比较直观的办法硬算,在老师看来这叫做诱敌深入,比如说一个题,求三阶导数或者五阶导数,直接算确实能算,但是不是最巧妙的,最快速的办法,老师就是想让考生在这儿花一些时间,可能这可以制造一些区分度吧。所以那些在考场上可以快速写完卷子的人,其实不是他们的手速有多快,可能手速也挺快,但不是核心因素,核心因素是解题方法的差异,我们高中年级第一最后去清华的那个同学,据说是发卷子的前五分钟,都还没动笔,第一面生物试卷都全部写完了,开始动笔填完选择题就可以直接翻页
原函数以什么为周期,导函数也以什么为周期
初等函数
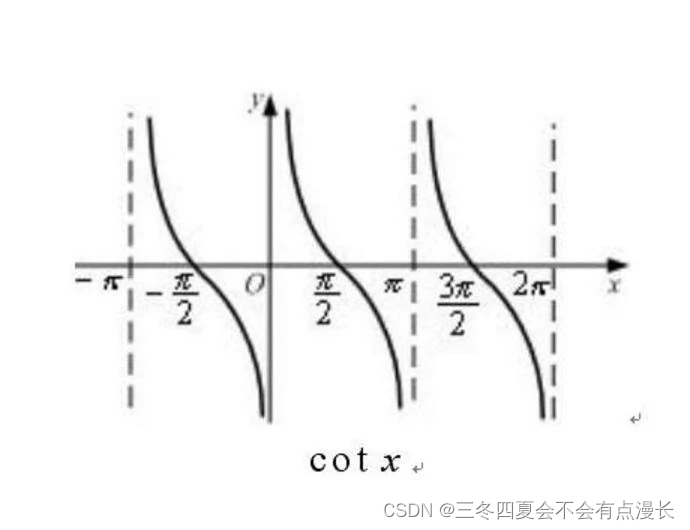
c
o
t
x
cot \ x
cot x 是奇函数
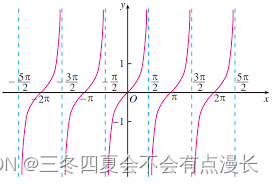
t a n x tan \ x tan x
三角函数里面的割函数确确实实用的相对较少,图像可以不用记住,但是计算的时候需要记住,
s
e
c
x
=
1
c
o
s
x
sec \ x=\frac{1}{cos \ x}
sec x=cos x1,数学公式用专业的语法确实会好看一些,下次也不要用 cos x 这种标记,代码这样子写还行,数学的就用这种
c
o
s
x
cos \ x
cos x ,注意是首字母不一样,求倒数就好,挺方便记忆的
s
e
c
2
x
=
1
+
t
a
n
2
x
sec ^2x=1+tan^2x
sec2x=1+tan2x
c
s
c
2
x
=
1
+
c
o
t
2
x
csc^2x=1+cot^2x
csc2x=1+cot2x
上面两个公式比较重要
知识过一遍记不住很正常,先留一个印象,以后需要用的时候,再去查就好了