🚀write in front🚀
📝个人主页：认真写博客的夏目浅石.
📣系列专栏：AcWing算法笔记

今天的月色好美

---

前言

这里介绍以下前缀和算法以及差分算法，用来梳理自己所学到的算法知识。

---

一、前缀和算法

1.1 什么是前缀和？

从我的理解角度来讲：前缀和就是高中数学当中的数列的求和Sn，差分就是前缀和的逆运算，就是递推公式。

1.2 一维前缀和

先来看一道题目吧：

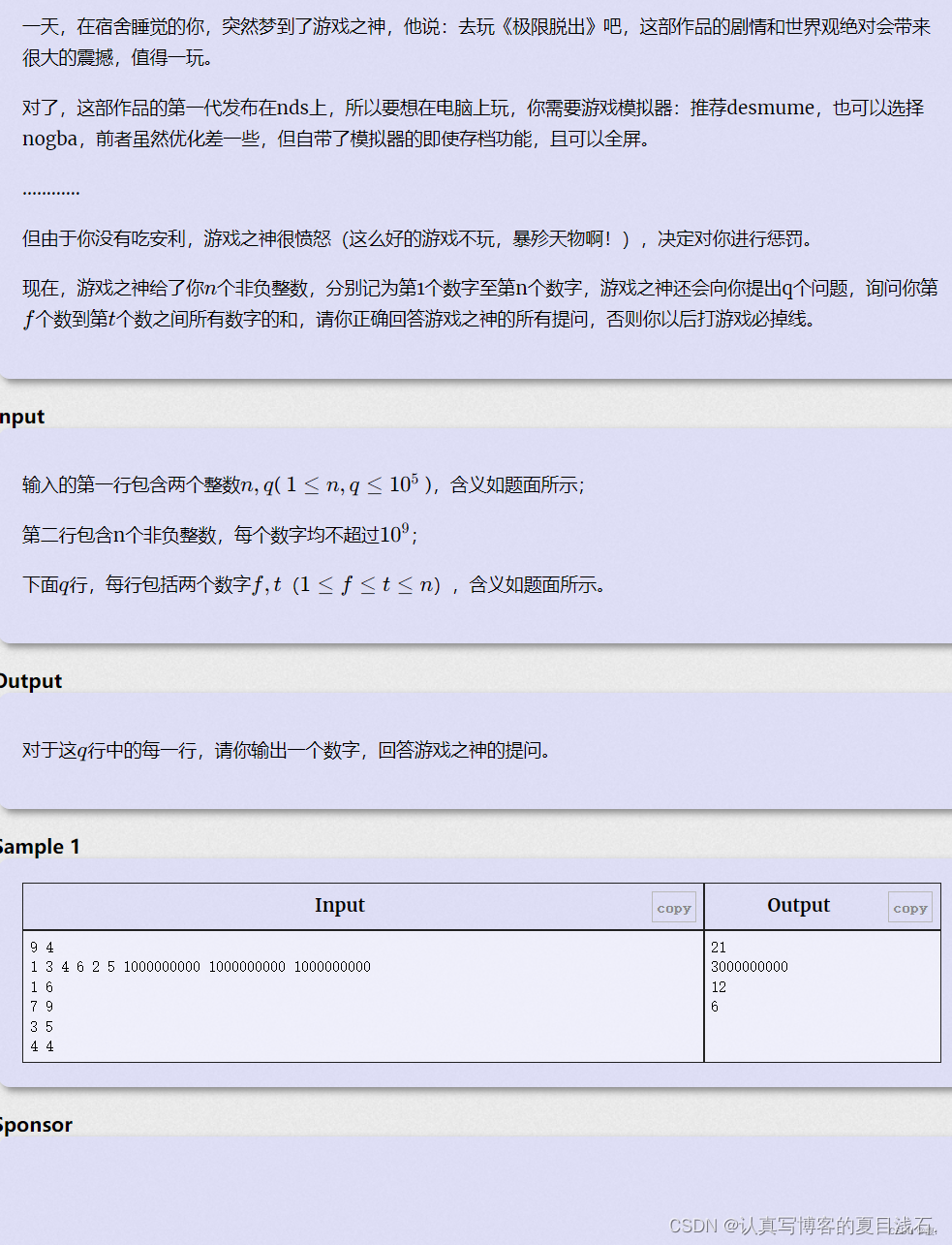
这是之前训练的时候的一道经典的前缀和问题，我们很容易想到暴力作法：遍历数组

代码如下：

#include<stdio.h>
const int N = 1e5 + 10;
int a[N];
int n,m;
int main()
{
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
	while(m--)
	{
    	int l, r;
    	int sum = 0;
    	scanf("%d%d", &l, &r);
    	for(int i = l; i <= r; i++)
    	{ 
     	   sum += a[i];
  	  	}
    	printf("%d\n",sum);
	}
	return 0;
}

这样的时间复杂度为O(n * m)，如果n和m的数据量稍微大一点就有可能超时，而我们如果使用前缀和的方法来做的话就能够将时间复杂度降到O(n + m)，大大提高了运算效率。

前缀和做法：

#include<stdio.h>
int main()
{
	long long n,k,arr[100010],sum[100010];
	scanf("%lld %lld",&n,&k);
	sum[0]=0;
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&arr[i]);
		int tmp=arr[i];
		sum[i]=tmp+sum[i-1];
	}
	for(int i=1;i<=k;i++)
	{
		int f,t;
		scanf("%d %d",&f,&t);
		printf("%lld\n",sum[t]-sum[f-1]);//重要步骤
	}
	return 0;
}

原理讲解：

sum[r] = a[1] + a[2] + a[3] + a[l-1] + a[l] + a[l + 1] .. a[r];
sum[l - 1] = a[1] + a[2] + a[3] + ... + a[l - 1];
sum[r] - sum[l - 1] = a[l] + a[l + 1] + ... + a[r];

这样，对于每个询问，只需要执行 sum[r] - sum[l - 1]。输出原序列中从第l个数到第r个数的和的时间复杂度变成了O(1)。

我们把它叫做一维前缀和。

二、二维前缀和

先来看一道题目吧：

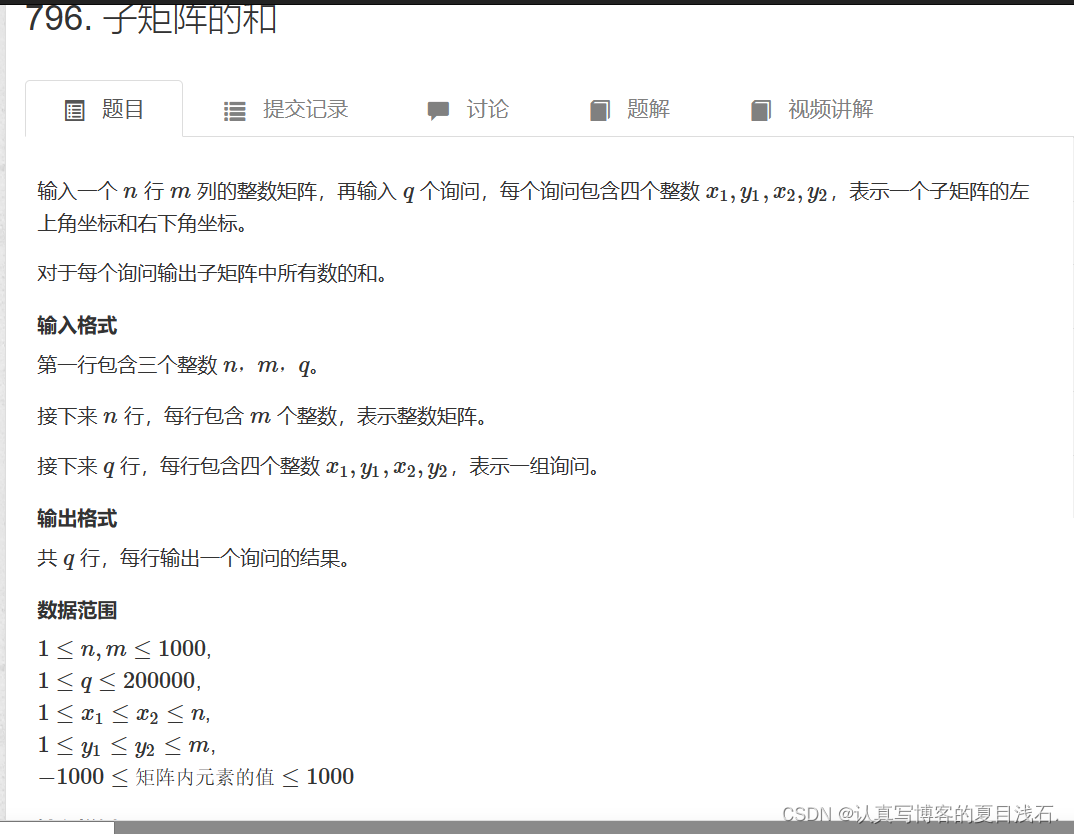
因为这里提及到了二维这个词，所以我们先来定义一个二维数组s[][] , s[i][j] 表示二维数组中，左上角(1, 1)到右下角(i, j)所包围的矩阵元素的和。接下来推导二维前缀和的公式。

先看一张图：

图解：

• (1,1)到(i,j-1)表示的面积是S1+S2定义为S黄蓝
• (1,1)到(i-1,j)表示的面积是S1+S3定义为S黄粉
• (1,1)到(i,j)表示的面积是S黄蓝+S黄粉-S1+S4

因此得出二维前缀和预处理公式

s[i][j] = s[i - 1][j] + s[i][j - 1 ] + a[i] [j] - s[i - 1][j - 1]

讲解完这些基础知识就可以去解决刚才的问题啦

#include <iostream>
using namespace std;
const int N = 1010;
int n, m, q;
int s[N][N];
int main()
{
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &s[i][j]);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
    while (q -- )
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }
    return 0;
}

所以总结模板就是：

S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

三、一维差分

先看一道问题：

类似于数学中的求导和积分，差分可以看成前缀和的逆运算。
首先给定一个原数组a：a[1], a[2] ， ， ， ， a[n];

然后我们构造一个数组b ： b[1], b[2] ， ， ， b[i];

使得 a[i] = b[1] + b[2] + ， ， ， + b[i]

也就是说，a数组是b数组的前缀和数组，反过来我们把b数组叫做a数组的差分数组。换句话说，每一个a[i]都是b数组中从头开始的一段区间和。

其实换个好理解的方式：
a[0 ]= 0;
b[1] = a[1] - a[0];
b[2] = a[2] - a[1];
…
b[n] = a[n] - a[n - 1];

但是知道了这些怎么用到题目上呢？或者换句话说，怎么就成为一种算法了呢？hhh下面就来解决这个问题哦~

如果给定区间[l, r ]，让我们把a数组中的[l, r] 区间中的每一个数都加上c,即 a[l] + c , a[l + 1] + c , a[l + 2] + c ,,,,,, a[r] + c;

暴力做法是for循环l到r区间，时间复杂度O(n)，如果我们需要对原数组执行m次这样的操作，时间复杂度就会变成O(n * m)。有没有更高效的做法吗? 考虑差分的做法。

首先让差分b数组中的 b[l] + c ,通过前缀和运算，a数组变成 a[l] + c ,a[l + 1] + c,,,,,, a[n] + c;

然后我们打个补丁，b[r + 1] - c, 通过前缀和运算，a数组变成 a[r + 1] - c,a[r + 2] - c,,,,,,,a[n] - c;

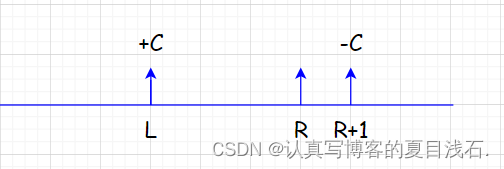
b[l] + c，效果使得a数组中 a[l] 及以后的数都加上了c(红色部分)，但我们只要求l到r 区间加上 c, 因此还需要执行 b[r + 1] - c,让a数组中 a[r + 1]及往后的区间再减去c(绿色部分)，这样对于a[r] 以后区间的数相当于没有发生改变。

因此我们得出一维差分结论：给a数组中的[ l, r] 区间中的每一个数都加上c,只需对差分数组b做 b[l] + = c,b[r+1] - = c 。时间复杂度为O(1), 大大提高了效率。

代码如下：

#include<stdio.h>
int main()
{
    int arr[100010],a[100010],n,m,q;
    scanf("%d%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&arr[i]);
    a[0]=0;
    for(int i=1;i<=n;i++)
    {
        a[i]=arr[i]-arr[i-1];
    }
    while(m--)
    {
        int l,r,c;
        scanf("%d%d%d",&l,&r,&c);
        a[l]+=c;
        a[r+1]-=c;
        
    }
    for(int i=1;i<=n;i++)
    {
        arr[i]=arr[i-1]+a[i];
        printf("%d ",arr[i]);
    }
    
    return 0;
}

四、二维差分

首先先看一道题目：

如果扩展到二维，我们需要让二维数组被选中的子矩阵中的每个元素的值加上c,是否也可以达到O(1)的时间复杂度。答案是可以的，考虑二维差分。

那么下面就来讲解二维差分

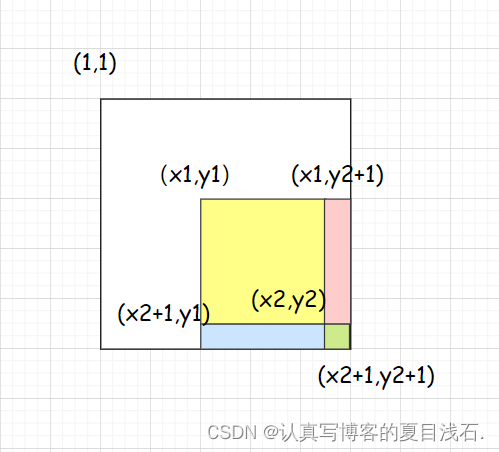
• b[x1][y1] += c ; 对应图1 ,让整个a数组中黄色矩形面积的元素都加上了c。
• b[x1,][y2 + 1] -= c ; 对应图2 ,让整个a数组中粉色+绿色矩形面积的元素再减去c，使其内元素不发生改变。
• b[x2 + 1][y1] -= c ; 对应图3 ,让整个a数组中蓝色+绿色矩形面积的元素再减去c，使其内元素不发生改变。
• b[x2 + 1][y2 + 1] += c; 对应图4,让整个a数组中绿色矩形面积的元素再加上c，绿色内的相当于被减了两次，再加上一次c，才能使其恢复。

模板：

void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1]+=c;
    b[x1][y2+1]-=c;
    b[x2+1][y1]-=c;
    b[x2+1][y2+1]+=c;
}

b[i][j] = a[i][j] − a[i − 1][j] − a[i][j − 1] + a[i −1 ][j − 1]
代码如下：

#include<iostream>
#include<cstdio>
using namespace std;

const int N = 1e3 + 10;
int a[N][N],b[N][N];
int n,m,q;

void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1]+=c;
    b[x1][y2+1]-=c;
    b[x2+1][y1]-=c;
    b[x2+1][y2+1]+=c;
}

int main()
{
    cin>>n>>m>>q;
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&a[i][j]);
        }
    }
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            insert(i,j,i,j,a[i][j]);//构造差分数组
        }
    }
    
    while(q--)
    {
        int x1,y1,x2,y2,c;
        cin>>x1>>y1>>x2>>y2>>c;
        insert(x1,y1,x2,y2,c);//进行差分
    }
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
        }
    }
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            printf("%d ",b[i][j]);
        }
        printf("\n");
    }

}

总结

今天学习了前缀和算法知识，每天进步一点点，不积硅步，无以至千里。
我们下期见吧~

如果无聊的话，就来逛逛我的博客栈吧stack-frame.cn

✨$原创不易，还希望各位大佬支持一下$

👍 $点赞，你的认可是我创作的动力！$

⭐️ $收藏，你的青睐是我努力的方向！$

✏️ $评论，你的意见是我进步的财富！$