写在前面

尽管这是一个几何问题，但本质上与3.1-矩阵连乘极为相似

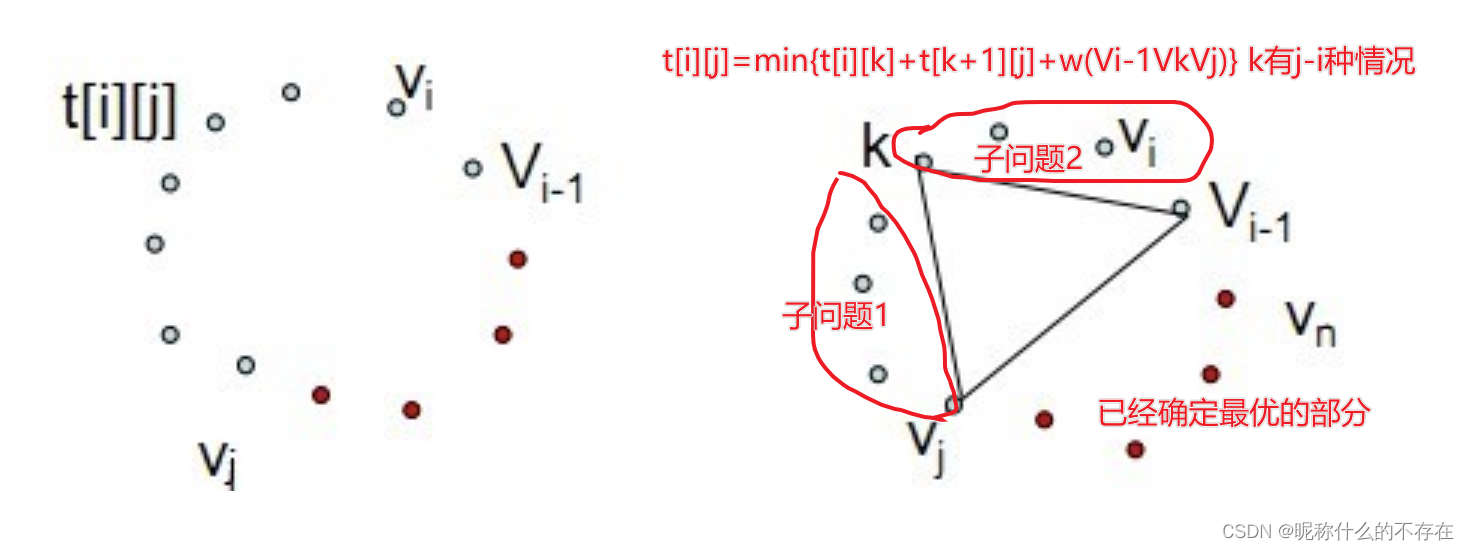
定义dp数组的含义：t[i][j]表述以点Vi-1，Vi，...，Vj为顶点的最优三角形剖分的最优权函数值

我们要计算的最优值在 t[1][n]

递归结构：凸多边形至少有三个顶点，一个三角形可以将这个多边形分为三个部分，合并起来的时候加上。

 

问题描述

多边形的边除了顶点没有别的交点，这就是一个简单的多边形。简单的多边形可以将平面分为三个部分：被包围在多边形内的所有点构成了多边形的内部，多边形本身构成多边形的边界，平面上其余被多边形包围的点构成了多边形的外部。

当一个简单多边形和其内部构成一个凸集时，则称该简单多边形为一个凸多边形。

用多边形顶点的逆时针序列表示凸多边形，即P={v0,v1,…,vn-1}表示具有n条边的凸多边形。

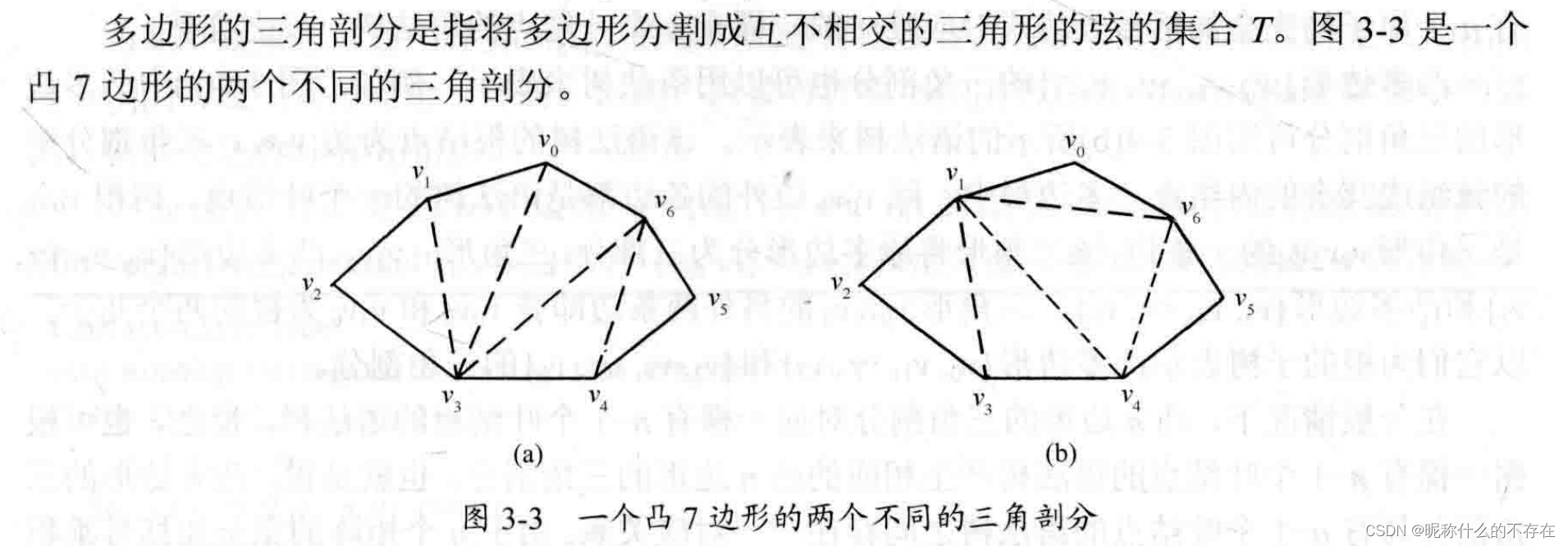
若vi与vj是多边形上不相邻的2个顶点，则线段vivj称为多边形的一条弦。

弦将多边形分割成2个多边形{vi,vi+1,…,vj}和{vj,vj+1,…vi}。

多边形的三角剖分是将多边形分割成互不相交的三角形的弦的集合T。

 

凸多边形问题：给定凸多边形P，以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分，使得即该三角剖分中诸三角形上权之和为最小。

可以定义三角形上各种各样的权函数w，对应这些权函数的最优三角形剖分为最小弦长三角形剖分。

问题分析

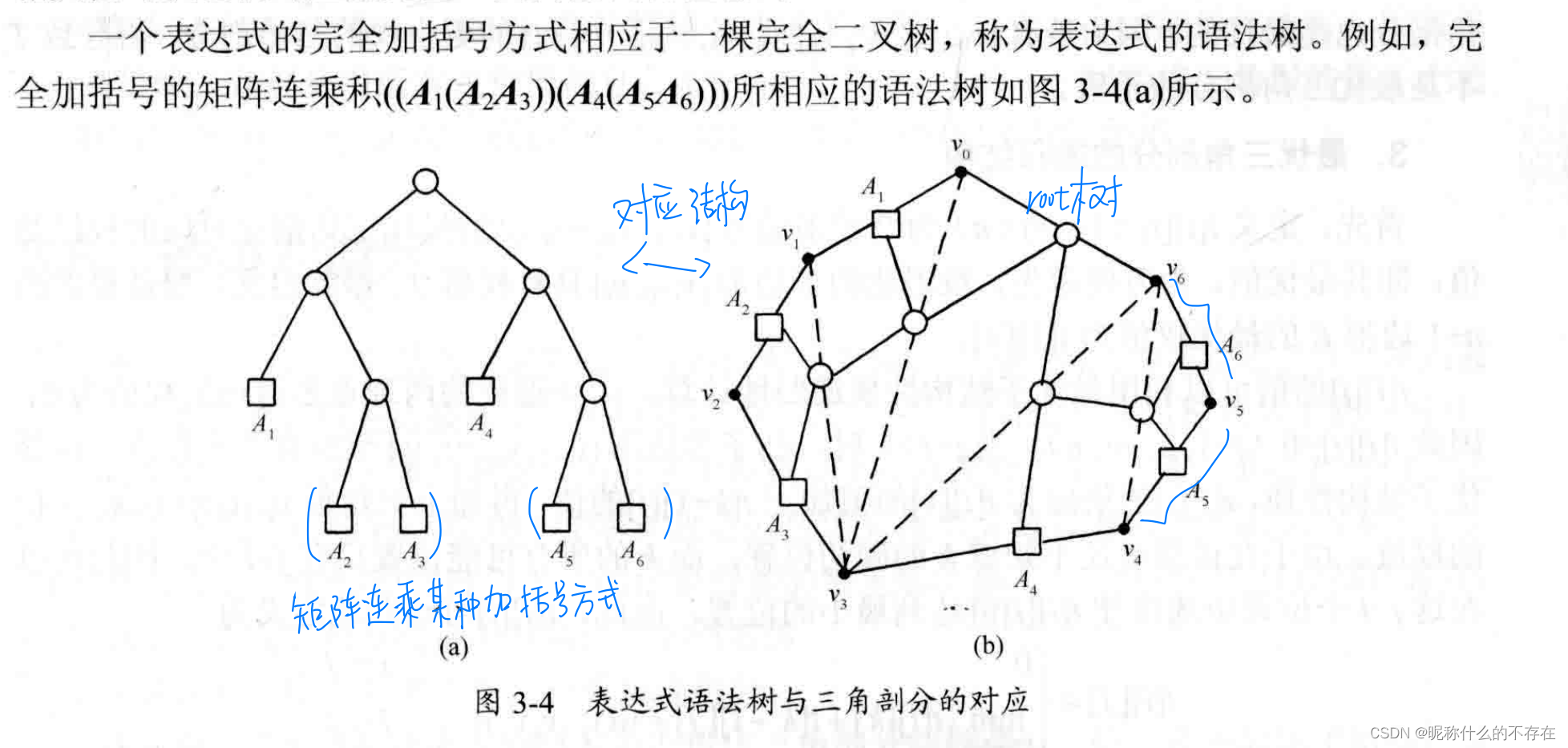
突变型三角形剖分和矩阵连乘加括号的方式联系紧密，二叉树有相同的性质。

 

一、最优子结构

凸多边形的最优三角剖分问题有最优子结构性质。

若凸(n+1)边形P={v0,v1,…,vn}的最优三角剖分T包含三角形v0vkvn，1≤k≤n-1，则T的权为3个部分权的和：三角形v0vkvn的权，子多边形{v0,v1,…,vk}和{vk,vk+1,…,vn}的权之和。

可以断言，由T所确定的这2个子多边形的三角剖分也是最优的。因为若有{v0,v1,…,vk}或{vk,vk+1,…,vn}的更小权的三角剖分将导致T不是最优三角剖分的矛盾。

二、递归结构（重要）

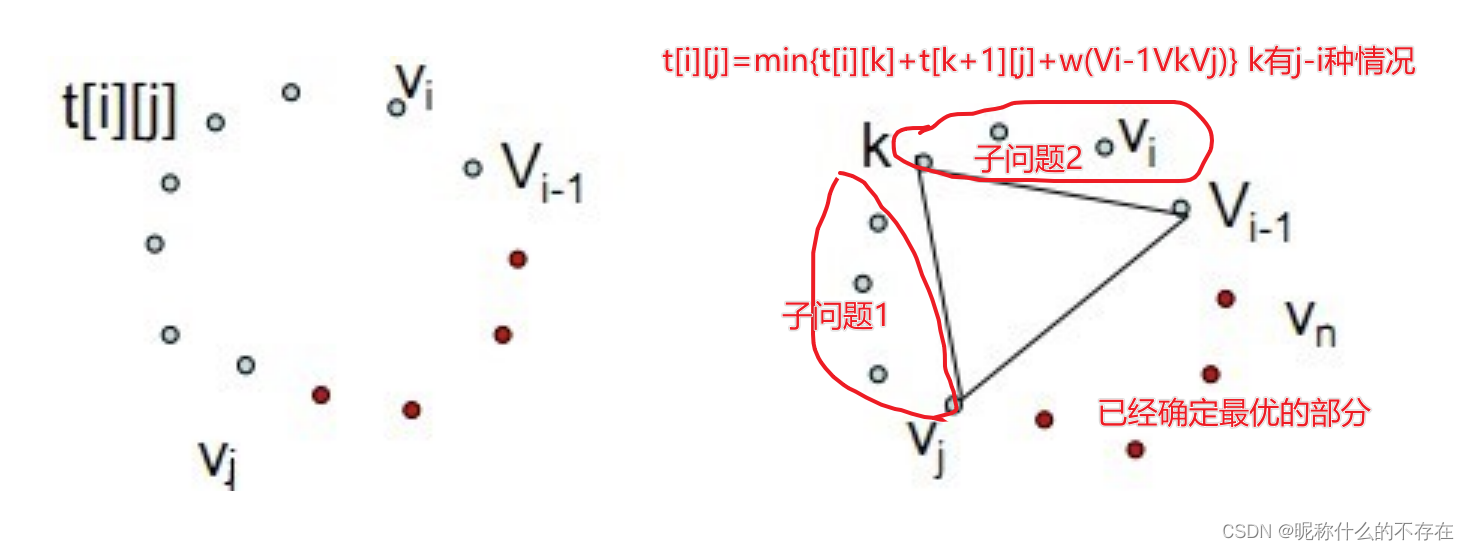
定义t[i][j]，1≤i<j≤n为凸子多边形{vi-1,vi,…,vj}的最优三角剖分所对应的权函数值，即其最优值。

为方便起见，设退化的多边形{vi-1,vi}具有权值0。

据此定义，要计算的凸(n+1)边形P的最优权值为t[1][n]。 t[i][j]的值可以利用最优子结构性质递归地计算。

当j-i≥1时，凸子多边形至少有3个顶点。由最优子结构性质，t[i][j]的值应为t[i][k]的值加上t[k+1][j]的值，再加上三角形vi-1vkvj的权值，其中i≤k≤j-1。

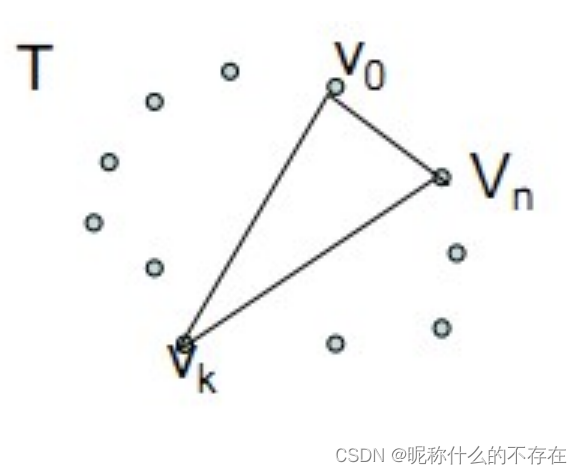
由于在计算时还不知道k的确切位置，而k的所有可能位置只有j-i个，因此可以在这j-i个位置中选出使t[i][j]值达到最小的位置。

 

三、自底向上计算并记录最优值

先求只有3个顶点凸多边形三角剖分的最优值，再求4个，直到n个。

四、构造最优解

需要从记录表中还原部分次序，找到最优剖分的弦，由这些弦构造出最优解。

算法设计：

（1）确定合适的数据结构

int n; //顶点数
int s[M][M];//记录最优策略二维数组
double t[M][M];//记录最优值二维数组
double weight[M][M];//记录各顶点之间权值的二维数组

（2）初始化

令n=n-1（顶点标号从v0开始），m[i][i]=0，s[i][i]=0。

（3）循环阶段

按照递归关系式计算3个顶点\{v_{i-1},v_i,v_{i+1}\}的最优三角剖分，j=i+1，将最优值存入m[i][j]，同时最优策略记入s[i][j]。

以此类推，直到求出所有顶点\{v_0,v_1,...,v_n\}的最优三角剖分，并将最优值存入m[1][n]，将最优策略记入s[1][n]。

（4）构造最优解

根据最优决策信息数组s[][]递归构造最优解，即输出凸多边形最优剖分的所有弦。s[1][n]表示凸多边形​​​​​​​\{v_0,v_1,...,v_n\}的最优三角剖分位置。

• 如果子问题1为空，即没有一个顶点，说明​​​​​​​v_0v_{s[1][n]}是一条边，不是弦，不需输出，否则输出。
• 如果子问题2为空，即没有一个顶点，说明​​​​​​​v_{s[1][n]}v_n是一条边，不是弦，不需输出，否则输出。
• 递归构造两个子问题，直到子问题为空。

#include<bits/stdc++.h>
using namespace std;
 
const int M =1111;
int n; //顶点数
int s[M][M];//记录最优策略二维数组
double t[M][M];//记录最优值二维数组
double weight[M][M];//记录各顶点之间权值的二维数组
 
void MinWeightTriangulation(){
    for (int i=1;i<=n;i++) //初始化
    {
        t[i][i]=0;
        s[i][i]=0;
    }
//r为问题规模，r=2实际上有三个点 r为当前计算的链长（子问题规模）  
    for(int r=2;r<=n;r++){
//n-r+1为最后一个r链的前边界  
        for (int i=1;i<=n-r+1;i++){
//计算前边界为r，链长为r的链的后边界  
            int j=i+r-1; 
//将链ij划分为A(i) * ( A[i+1:j] )这里实际上就是k=i
            t[i][j]=t[i+1][j]+weight[i-1][i]+weight[i][j]+weight[i-1][j];
//策略为k=i的情况
            s[i][j]=i;
//枚举划分点i到j所有情况
            for (int k=i+1;k<j;k++){
//将链ij划分为( A[i:k] )* (A[k+1:j])
                double u=t[i][k]+t[k+1][j]+weight[i-1][k]+weight[k][j]+weight[i-1][j];
                if(t[i][j]>u){
                    t[i][j]=u;
                    s[i][j]=k;
                }
            }
        }
    }
}
//递归求解所有子问题的弦。 
void Traceback(int i,int j) 
{
    if(i==j)
        return ;
    Traceback(i,s[i][j]);
    Traceback(s[i][j]+1,j);
    cout<<"三角剖分顶点：V"<<i-1<<",V"<<j<<",V"<<s[i][j]<<endl;
}
 
int main()
{
    int i;
    int j;
    cout << "请输入顶点个数n："<< endl;
    cin >> n;
    n--;
    cout << "请依次输入各顶点的连接权值：" << endl;
    for (i=0;i<=n;++i)
    {
        for (j=0;j<=n;++j)
        {
            cin >> weight[i][j];
        }
    }
    MinWeightTriangulation();
    cout << "最优三角剖分的权值和是:" << endl;
    cout << t[1][n]<< endl;
    cout << "三角剖分顶点："<< endl;
    Traceback(1,n);
    return 0;
}

 类似矩阵连乘，简单分析一下即可，计算最优次序类型的。