作者: 华丞臧
专栏:【数据结构】
各位读者老爷如果觉得博主写的不错,请诸位多多支持(点赞+收藏+关注)。如果有错误的地方,欢迎在评论区指出。
推荐一款刷题网站 👉 LeetCode刷题网站
目录
前言
一、二叉树的链式结构
二、二叉树链式结构的实现
2.1 前序遍历
2.2 中序遍历
2.3 后序遍历
2.4 层序遍历
2.5 二叉树节点个数
2.6 二叉树叶子节点个数
2.7 二叉树第k层节点个数
2.8 二叉树的高度
2.9 二叉树查找值为x的节点
2.10 通过前序遍历的数组构建二叉树
2.11 判断二叉树是否是完全二叉树
2.12 二叉树销毁
三、完整代码及测试
3.1 BTree.h
3.2 BinaryTreeNode.c
3.3 test.c
3.4 测试
前言
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是 链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所 在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链。
一、二叉树的链式结构
//二叉链结构
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
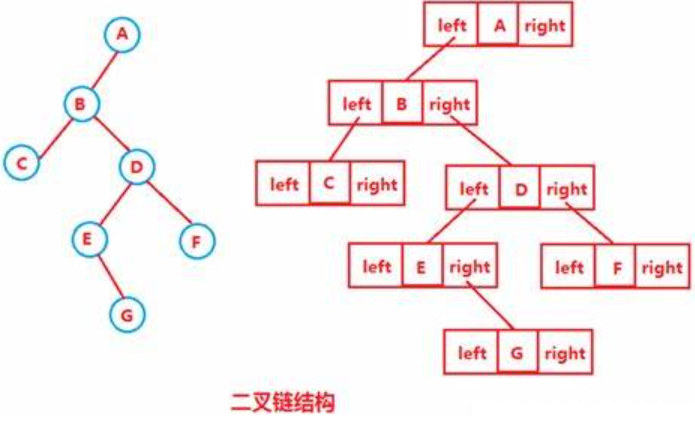
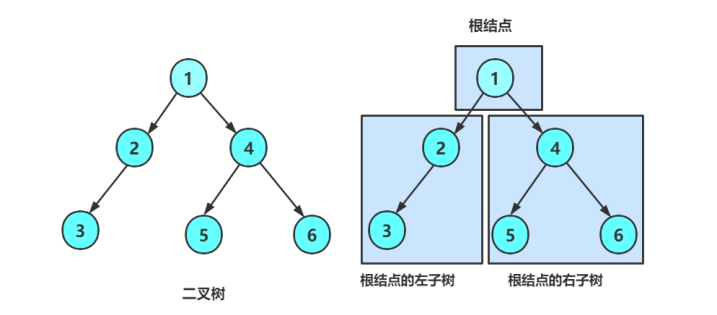
回顾二叉树的概念,二叉树是:
- 空树
- 非空树:根节点及其左右子树构成。
- 树的定义是递归式的。
二、二叉树链式结构的实现
学习二叉树的结构,最简单的方式就是遍历。所谓遍历就是按照某种特定规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
2.1 前序遍历
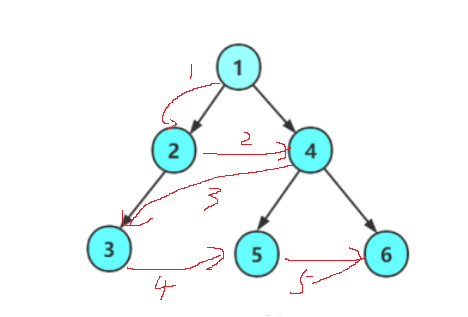
前序遍历(Preorder Traversal 亦称先序遍历,先根遍历)——访问根结点的操作发生在遍历其左右子树之前。
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
//assert(root);
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->data); //先访问根结点
BinaryTreePrevOrder(root->left); //递归左子树
BinaryTreePrevOrder(root->right); //递归右子树
}2.2 中序遍历
中序遍历(Inorder Traversal,又称中根遍历)——访问根结点的操作发生在遍历其左右子树之中(间)。
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
BinaryTreeInOrder(root->left);
printf("%d ",root->data);
BinaryTreeInOrder(root->right);
}2.3 后序遍历
后序遍历(Postorder Traversal,又称后根遍历)——访问根结点的操作发生在遍历其左右子树之后。
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
BinaryTreePostOrder(root->left);
BinaryTreePostOrder(root->right);
printf("%d ",root->data);
}2.4 层序遍历
除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在 层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层 上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
需要使用队列来实现层序遍历,先把根节点入队列,每访问队列首元素后再把其出队列,并且把该节点的左右节点入队列;一直循环知道队列为空结束。
队列代码👉队列代码
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
Queue p;
QueueInit(&p);
QueuePush(&p, root);
while (!QueueEmpty(&p))
{
root = QueueFront(&p);
printf("%d ", root->data);
QueuePop(&p);
QueuePush(&p, root->left);
QueuePush(&p, root->right);
}
printf("\n");
QueueDestroy(&p);
}2.5 二叉树节点个数
二叉树的节点个数等于根节点加左子树和右子树的节点个数,而左右子树节点个数又是根节点加左子树和右子树。
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
//改良
//return root == NULL ? 0 :
TreeSize(root->left) + TreeSize(root->right) + 1;
}2.6 二叉树叶子节点个数
叶节点就是左右子树都为空树的节点,一棵树的叶子节点就等于左子树叶子节点加上右子树叶子节点。
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left)
+ BinaryTreeLeafSize(root->right);
}2.7 二叉树第k层节点个数
转换成递归k-1。当递归到k=1时,此时节点就是第k层的节点。
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left,k-1)
+ BinaryTreeLevelKSize(root->right, k - 1);
}2.8 二叉树的高度
一颗二叉树的高度等于左右子树高度大的那个加一。
//二叉树的高度
int BinaryTreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int left = BinaryTreeHeight(root->left);
int right = BinaryTreeHeight(root->right);
return left > right ? left + 1 : right + 1;
}2.9 二叉树查找值为x的节点
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* retleft = BinaryTreeFind(root->left,x);
BTNode* retright = BinaryTreeFind(root->right, x);
if (retleft != NULL)
{
return retleft;
}
else if(retright != NULL)
{
return retright;
}
else
{
return NULL;
}
}2.10 通过前序遍历的数组构建二叉树
注意需要用一个指针来控制数组a的移动,这样可以实现依次读取数组a里面的值,指针可以在递归的时候改变变量的值。
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root= (BTNode*)malloc(sizeof(BTNode));
if (root == NULL)
{
perror("malloc fail");
exit(-1);
}
root->data = a[*pi];
(*pi)++;
root->left = BinaryTreeCreate(a, pi);
root->right = BinaryTreeCreate(a, pi);
return root;
}2.11 判断二叉树是否是完全二叉树
需要利用队列这个数据结构来实现。
与层序遍历类似,先把根节点入队列,每访问队列首元素后再把其出队列,并且把该节点的左右节点入队列,只不过当节点为NULL时也需要入队列;当首元素出队列为NULL指针时,需要判断之后是否还会出现不为NULL指针的节点,如果出现,则不是完全二叉树返回false;如果没出,则是完全二叉树返回true。
队列代码👉队列代码
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{
Queue pq;
QueueInit(&pq);
int flag = 0;
QueuePush(&pq,root);
while (!QueueEmpty(&pq))
{
root = QueueFront(&pq);
if (root == NULL)
{
flag = 1;
}
if (flag == 1 && root != NULL)
{
QueueDestroy(&pq);
return false;
}
QueuePop(&pq);
if (root != NULL)
QueuePush(&pq, root->left);
if (root != NULL)
QueuePush(&pq, root->right);
}
QueueDestroy(&pq);
return true;
}2.12 二叉树销毁
销毁二叉树需要后序遍历,先访问根节点的左右子树再销毁根节点。
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);
}三、完整代码及测试
全部代码👉队列+二叉树链式结构全部代码
3.1 BTree.h
#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(BTDataType x);
// 通过前序遍历的数组构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);
//二叉树的高度
int BinaryTreeHeight(BTNode* root);
3.2 BinaryTreeNode.c
#include "BTree.h"
#include "Queue.h"
BTNode* BuyNode(BTDataType x)
{
BTNode* tmp = (BTNode*)malloc(sizeof(BTNode));
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
tmp->data = x;
tmp->left = NULL;
tmp->right = NULL;
return tmp;
}
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
//assert(root);
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->data);
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
BinaryTreeInOrder(root->left);
printf("%d ",root->data);
BinaryTreeInOrder(root->right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
BinaryTreePostOrder(root->left);
BinaryTreePostOrder(root->right);
printf("%d ",root->data);
}
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
//return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
int count = BinaryTreeLeafSize(root->left)
+ BinaryTreeLeafSize(root->right);
return count;
}
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left,k-1)
+ BinaryTreeLevelKSize(root->right, k - 1);
}
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTNode* retleft = BinaryTreeFind(root->left,x);
BTNode* retright = BinaryTreeFind(root->right, x);
if (retleft != NULL)
{
return retleft;
}
else if(retright != NULL)
{
return retright;
}
else
{
return NULL;
}
}
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{
Queue pq;
QueueInit(&pq);
int flag = 0;
QueuePush(&pq,root);
while (!QueueEmpty(&pq))
{
root = QueueFront(&pq);
if (root == NULL)
{
flag = 1;
}
if (flag == 1 && root != NULL)
{
QueueDestroy(&pq);
return false;
}
QueuePop(&pq);
if (root != NULL)
QueuePush(&pq, root->left);
if (root != NULL)
QueuePush(&pq, root->right);
}
QueueDestroy(&pq);
return true;
}
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
Queue p;
QueueInit(&p);
QueuePush(&p, root);
while (!QueueEmpty(&p))
{
BTNode* front = QueueFront(&p);
QueuePop(&p);
printf("%d ", front->data);
if(front->left != NULL)
QueuePush(&p, front->left);
if (front->right != NULL)
QueuePush(&p, front->right);
}
printf("\n");
QueueDestroy(&p);
}
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root= (BTNode*)malloc(sizeof(BTNode));
if (root == NULL)
{
perror("malloc fail");
exit(-1);
}
root->data = a[*pi];
(*pi)++;
root->left = BinaryTreeCreate(a, pi);
root->right = BinaryTreeCreate(a, pi);
return root;
}
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);
}
//二叉树的高度
int BinaryTreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int left = BinaryTreeHeight(root->left);
int right = BinaryTreeHeight(root->right);
return left > right ? left + 1 : right + 1;
}3.3 test.c
#include "BTree.h"
#include "Queue.h"
BTNode* CreatBinaryTree()
{
BTNode* n1 = BuyNode(1);
BTNode* n2 = BuyNode(2);
BTNode* n3 = BuyNode(3);
BTNode* n4 = BuyNode(4);
BTNode* n5 = BuyNode(5);
BTNode* n6 = BuyNode(6);
BTNode* n7 = BuyNode(7);
n1->left = n2;
n1->right = n4;
n2->left = n3;
n2->right = n7;
n4->left = n5;
n4->right = n6;
/*n2->right = NULL;
n3->right = NULL;
n3->left = NULL;
n5->right = NULL;
n5->left = NULL;
n6->right = NULL;
n6->left = NULL;*/
return n1;
}
int main()
{
BTNode* root = CreatBinaryTree();
//BTNode* root = NULL;
printf("前序:");
BinaryTreePrevOrder(root);
printf("\n");
printf("中序:");
BinaryTreeInOrder(root);
printf("\n");
printf("后序:");
BinaryTreePostOrder(root);
printf("\n");
printf("TreeSize = %d\n", BinaryTreeSize(root));
printf("TreeLeafSize = %d\n", BinaryTreeLeafSize(root));
printf("Level K Size = %d\n", BinaryTreeLevelKSize(root,1));
printf("TreeHeight = %d\n", BinaryTreeHeight(root));
BTNode* tmp = BinaryTreeFind(root, 7);
if (tmp == NULL)
{
perror("TreeFind = BinaryTreeFind fail");
return -1;
}
printf("%d\n",tmp->data);
printf("层序:");
BinaryTreeLevelOrder(root);
if (BinaryTreeComplete(root))
{
printf("BinaryTreeComplete:true\n");
}
else
{
printf("BinaryTreeComplete:false\n");
}
return 0;
}3.4 测试
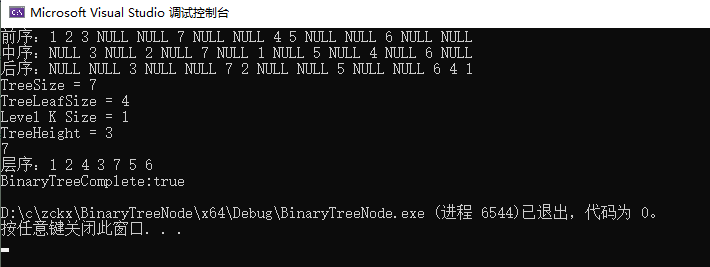





![[附源码]java毕业设计农村政务管理系统](https://img-blog.csdnimg.cn/4d9fd7dff9ee49aea8b3469489c314bb.png)
![[附源码]SSM计算机毕业设计智慧农业销售平台JAVA](https://img-blog.csdnimg.cn/a32532b5ab8e44ec917408b98bd99cf5.png)