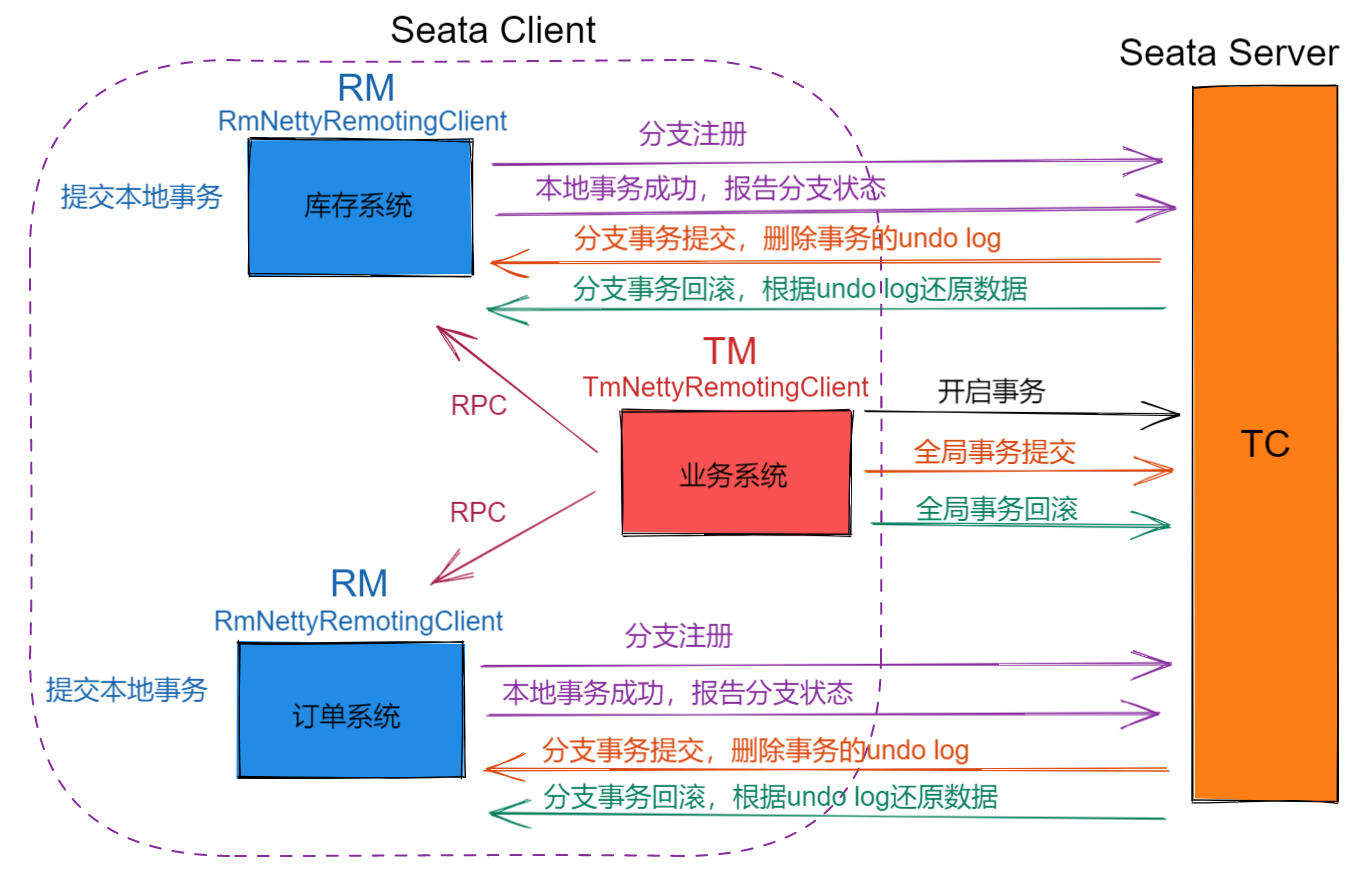
数据分析经典算法——红黑树
- 红黑树的重要性
- 红黑树的定义
- 红黑树图解
红黑树的重要性
红黑树的优势 红黑树能够以O(log2(N))的时间复杂度的时间复杂度进行搜索、插入、删除操作。 此外,任何不平衡都会在3次旋转之内解决。 这一点是AVL所不具备的。 而且实际应用中,很多语言都实现了红黑树的数据结构。
红黑树的定义
红黑树是特殊的平衡二叉树。遵循红定理和黑定理。红定理:在一条路径上不能出现两个相连的红节点;黑定理:根节点必须是黑节点,而且所有节点通向树的尾端的路径上,所含的黑节点的个数必须相等。
红黑树图解
我们看一看一个典型的红黑树到底是什么样儿?
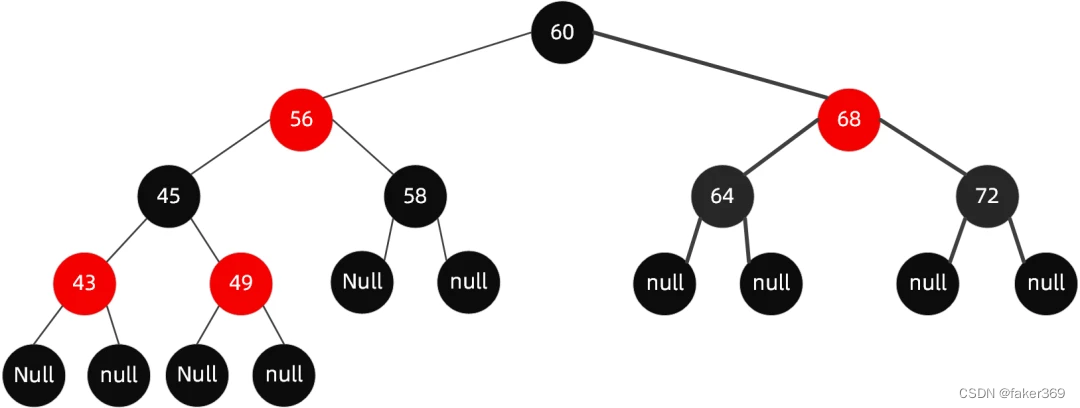
首先解读一下规则,除了字面上看到的意思,还隐藏了哪些意思呢?
从根节点到叶子节点的最长路径不大于最短路径的 2 倍
怎么样的路径算最短路径?从规则 5 中,我们知道从根节点到每个叶子节点的黑色节点数量是一样的,那么纯由黑色节点组成的路径就是最短路径。
什么样的路径算是最长路径?根据规则 4 和规则 3,若有红色节点,则必然有一个连接的黑色节点,当红色节点和黑色节点数量相同时,就是最长路径,也就是黑色节点(或红色节点)*2。
为什么说新加入到红黑树中的节点为红色节点
从规则 4 中知道,当前红黑树中从根节点到每个叶子节点的黑色节点数量是一样的,此时假如新的是黑色节点的话,必然破坏规则。
但加入红色节点却不一定,除非其父节点就是红色节点,因此加入红色节点,破坏规则的可能性小一些,下面我们也会举例来说明。
什么情况下,红黑树的结构会被破坏呢?破坏后又怎么维持平衡,维持平衡主要通过两种方式【变色】和【旋转】,【旋转】又分【左旋】和【右旋】,两种方式可相互结合。
下面我们从插入和删除两种场景来举例说明。
红黑树节点插入
当我们插入值为 66 的节点时,红黑树变成了这样:
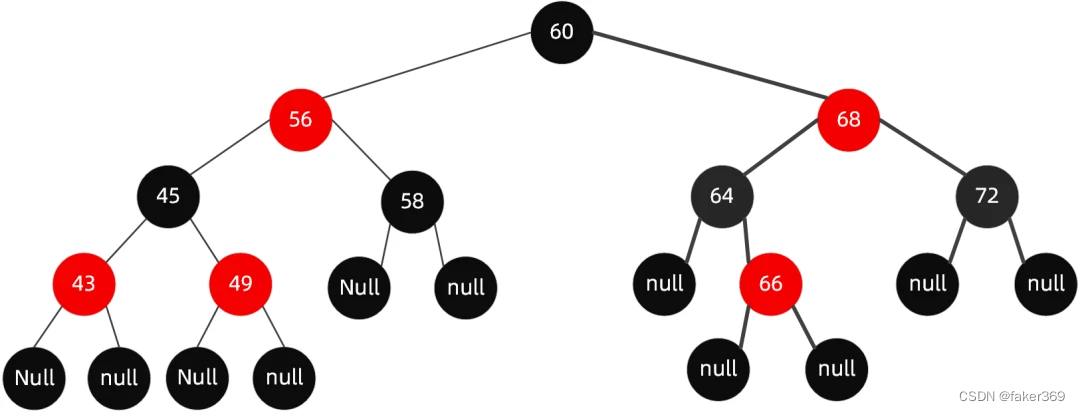
很明显,这个时候结构依然遵循着上述 6 大规则,无需启动自动平衡机制调整节点平衡状态。
如果再向里面插入值为 51 的节点,这个时候红黑树变成了这样:
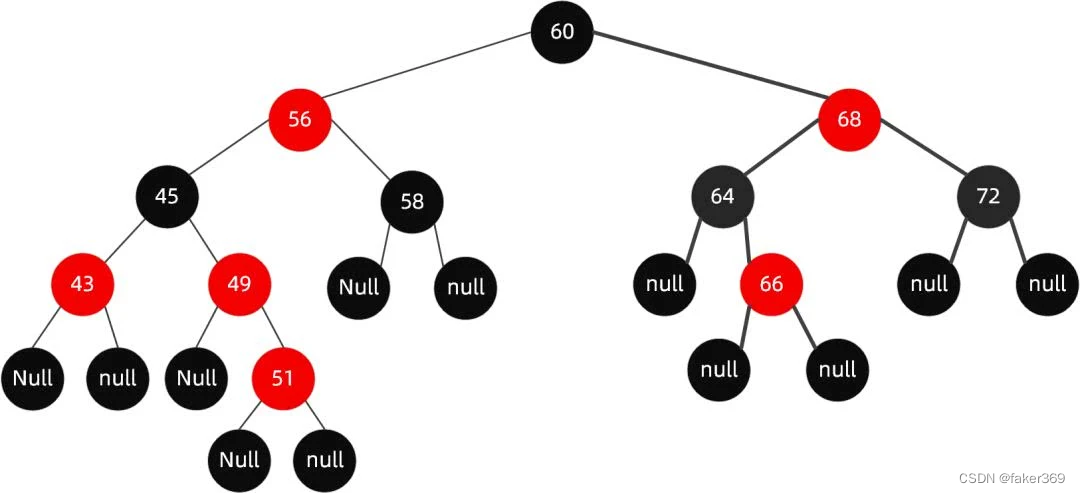
很明显现在的结构不遵循规则 4 了,这个时候就需要启动自动平衡机制调整节点平衡状态。
变色
我们可以通过变色的方式,使结构满足红黑树的规则:
首先解决结构不遵循规则 4 这一点(红色节点相连,节点 49-51),需将节点 49 改为黑色。
此时我们发现又违反了规则 5(56-49-51-XX 路径中黑色节点超过了其他路径),那么我们将节点 45 改为红色节点。
哈哈,妹的,又违反了规则 4(红色节点相连,节点 56-45-43),那么我们将节点 56 和节点 43 改为黑色节点。
但是我们发现此时又违反了规则 5(60-56-XX 路径的黑色节点比 60-68-XX 的黑色节点多),因此我们需要调整节点 68 为黑色。
完成!
最终调整完成后的树为:
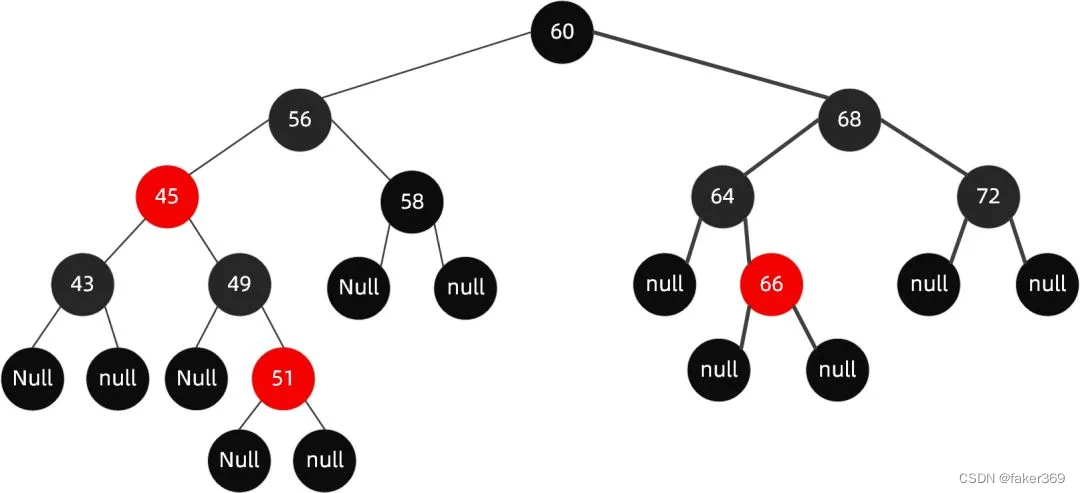
但并不是什么时候都那么幸运,可以直接通过变色就达成目的,大多数时候还需要通过旋转来解决。
如在下面这棵树的基础上,加入节点 65:
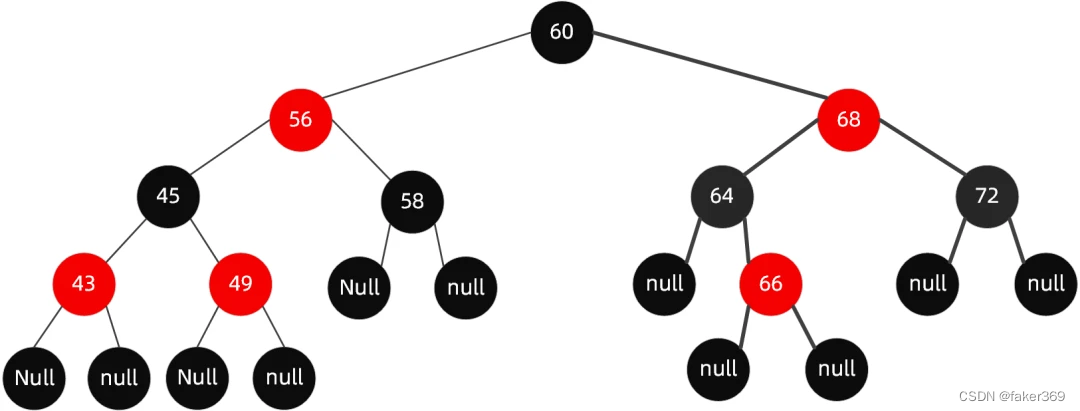
插入节点 65 后进行以下步骤:
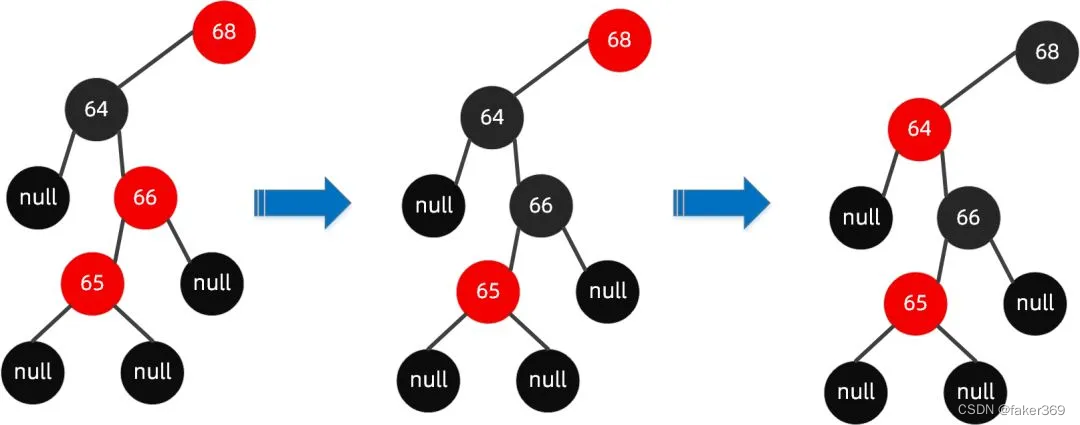
这个时候,你会发现对于节点 64 无论是红色节点还是黑色节点,都会违反规则 5,路径中的黑色节点始终无法达成一致,这个时候仅通过【变色】已经无法达成目的。
我们需要通过旋转操作,当然【旋转】操作一般还需要搭配【变色】操作。旋转包括【左旋】和【右旋】。
左旋:逆时针旋转两个节点,让一个节点被其右子节点取代,而该节点成为右子节点的左子节点。
左旋操作步骤如下:首先断开节点 PL 与右子节点 G 的关系,同时将其右子节点的引用指向节点 C2;然后断开节点 G 与左子节点 C2 的关系,同时将 G 的左子节点的应用指向节点 PL。
右旋:顺时针旋转两个节点,让一个节点被其左子节点取代,而该节点成为左子节点的右子节点。
右旋操作步骤如下:首先断开节点 G 与左子节点 PL 的关系,同时将其左子节点的引用指向节点 C2;然后断开节点 PL 与右子节点 C2 的关系,同时将 PL 的右子节点的应用指向节点 G。
无法通过变色而进行旋转的场景分为以下四种:
左左节点旋转
这种情况下,父节点和插入的节点都是左节点,如下图(旋转原始图1)这种情况下,我们要插入节点 65。
规则如下:以祖父节点【右旋】,搭配【变色】。
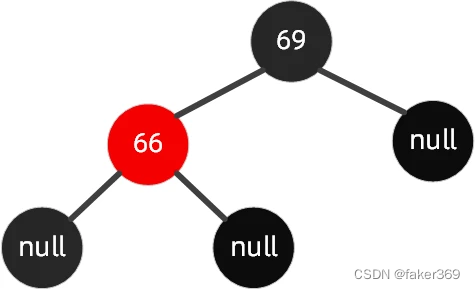
按照规则,步骤如下:
左右节点旋转
这种情况下,父节点是左节点,插入的节点是右节点,在旋转原始图 1 中,我们要插入节点 67。
规则如下:先父节点【左旋】,然后祖父节点【右旋】,搭配【变色】。
按照规则,步骤如下:
右左节点旋转
这种情况下,父节点是右节点,插入的节点是左节点,如下图(旋转原始图 2)这种情况,我们要插入节点 68。
规则如下:先父节点【右旋】,然后祖父节点【左旋】,搭配【变色】。
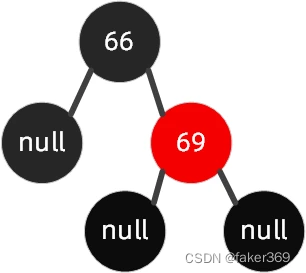
按照规则,步骤如下:
右右节点旋转
这种情况下,父节点和插入的节点都是右节点,在旋转原始图 2 中,我们要插入节点 70。
规则如下:以祖父节点【左旋】,搭配【变色】。
按照规则,步骤如下:
红黑树插入总结
红黑树插入总结如下图:
红黑树节点删除
相比较于红黑树的节点插入,删除节点更为复杂,我们从子节点是否为 null 和红色为思考维度来讨论。
子节点至少有一个为 null
当待删除的节点的子节点至少有一个为 null 节点时,删除了该节点后,将其有值的节点取代当前节点即可。
若都为 null,则将当前节点设置为 null,当然如果违反规则了,则按需调整,如【变色】以及【旋转】。
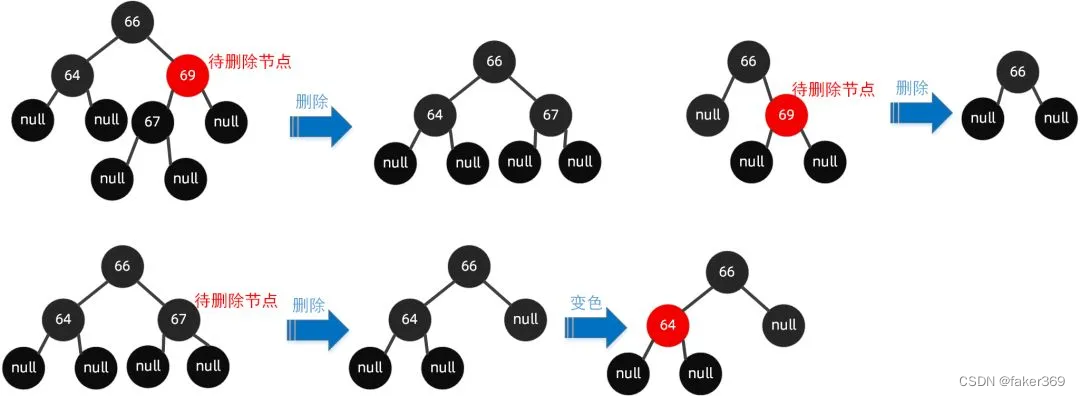
子节点都是非 null 节点
这种情况下,第一步:找到该节点的前驱或者后继。
前驱:左子树中值最大的节点(可得出其最多只有一个非 null 子节点,可能都为 null)。
后继:右子树中值最小的节点(可得出其最多只有一个非 null 子节点,可能都为 null)。
前驱和后继都是值最接近该节点值的节点,类似于该节点.prev=前驱,该节点.next=后继。
第二步:将前驱或者后继的值复制到该节点中,然后删掉前驱或者后继。
如果删除的是左节点,则将前驱的值复制到该节点中,然后删除前驱;如果删除的是右节点,则将后继的值复制到该节点中,然后删除后继。
这相当于是一种“取巧”的方法,我们删除节点的目的是使该节点的值在红黑树上不存在。
因此专注于该目的,我们并不关注删除节点时是否真是我们想删除的那个节点,同时我们也不需考虑树结构的变化,因为树的结构本身就会因为自动平衡机制而经常进行调整。
前面我们已经说了,我们要删除的实际上是前驱或者后继,因此我们就以前驱为主线来讲解。
后继的学习可参考前驱,包括下面几种情况:
前驱为黑色节点,并且有一个非 null 子节点
分析:因为要删除的是左节点 64,找到该节点的前驱 63;然后用前驱的值 63替换待删除节点的值 64,此时两个节点(待删除节点和前驱)的值都为 63;
删除前驱 63,此时成为上图过程中间环节,但我们发现其不符合红黑树规则 4,因此需要进行自动平衡调整。这里直接通过【变色】即可完成。
前驱为黑色节点,同时子节点都为 null
分析:因为要删除的是左节点 64,找到该节点的前驱 63;然后用前驱的值 63 替换待删除节点的值 64,此时两个节点(待删除节点和前驱)的值都为 63。
删除前驱 63,此时成为上图过程中间环节,但我们发现其不符合红黑树规则 5,因此需要进行自动平衡调整。这里直接通过【变色】即可完成。
前驱为红色节点,同时子节点都为 null
分析:因为要删除的是左节点 64,找到该节点的前驱 63;然后用前驱的值 63替换待删除节点的值 64,此时两个节点(待删除节点和前驱)的值都为 63;删除前驱 63,树的结构并没有打破规则。
红黑树删除总结
红黑树删除的情况比较多,但也就存在以下情况:
删除的是根节点,则直接将根节点置为 null。
待删除节点的左右子节点都为 null,删除时将该节点置为 null。
待删除节点的左右子节点有一个有值,则用有值的节点替换该节点即可。
待删除节点的左右子节点都不为 null,则找前驱或者后继,将前驱或者后继的值复制到该节点中,然后删除前驱或者后继。
节点删除后可能会造成红黑树的不平衡,这时我们需通过【变色】+【旋转】的方式来调整,使之平衡




![[附源码]java毕业设计农村政务管理系统](https://img-blog.csdnimg.cn/4d9fd7dff9ee49aea8b3469489c314bb.png)
![[附源码]SSM计算机毕业设计智慧农业销售平台JAVA](https://img-blog.csdnimg.cn/a32532b5ab8e44ec917408b98bd99cf5.png)