算法概念

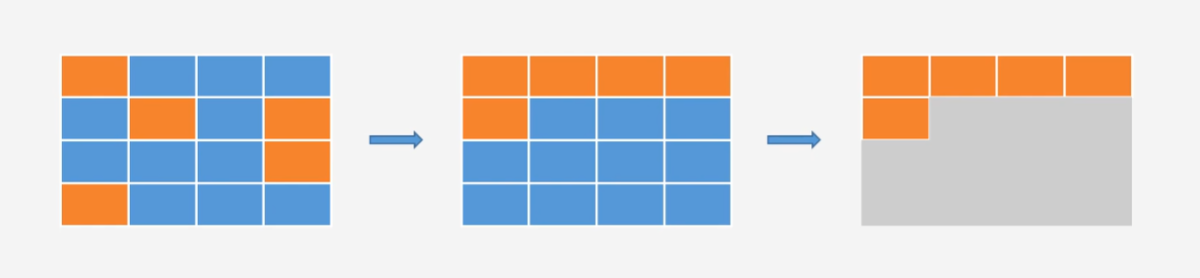
• 分治算法（divide and conquer）算法的核心思想其实就是"分而治之"，将原问题划分成n个规模较小，并且结构与原问题相似的子问题，递归地解决这些子问题，然后再合并其结果，然后就会得到原问题的解。
• 分治和递归的区别：分治算法是种处理问题的思想，递归式一种编程技巧。
• 分治算法的递归实现中，每一层递归都会涉及三个操作：
  分解：将原问题分解成一系列子问题；
  解决：递归地求解各个子问题，若子问题足够小，则直接求解；
  合并：将子问题地结果合并成原问题。

分治算法典型地例子就是归并排序，具体请参考本人另一篇博客：算法（十）归并排序

算法例子

字符串中小写转大写

将字符串中的小写字母转化为大写字母，“abcde”转化为"ABCDE"，我们可以利用分治的思想将整个字符串转化成一个一个的字符处理。

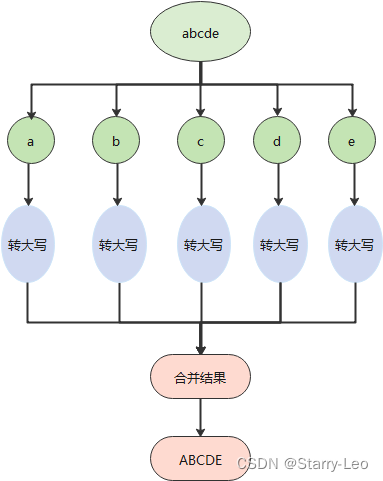
代码实现：

package com.xxliao.algorithms.divide_conquer;

/**
 * @author xxliao
 * @description: 将字符串中的小写字母转化为大写字母
 * “abcde”转化为"ABCDE"
 * 我们可以利用分治的思想将整个字符串转化成一个一个的字符处理
 * @date 2024/5/31 21:35
 */

public class Demo01 {

    public static void main(String[] args) {
        String ss="abcde";
        System.out.println(toUpCase(ss.toCharArray(),0));
    }

    /**
     * @description  将char[] 中小写字母转大写字母
     * @author  xxliao
     * @date  2024/5/31 21:39
     */
    public static char[] toUpCase(char[] array,int i){
        if(i>=array.length)
            // 递归结束条件
            return array;
        // 解决：递归地求解各个子问题，若子问题足够小，则直接求解
        array[i]=toUpCaseUnit(array[i]);
        // 向下递归
        return toUpCase(array,i+1);
    }

    /**
     * @description  char字符，小写转大写
     * @author  xxliao
     * @date  2024/5/31 21:39
     */
    public static char toUpCaseUnit(char c){
        int n=c;
        if (n<97 || n>122){
            return ' ';
        }
        return (char)Integer.parseInt(String.valueOf(n-32));
    }
}

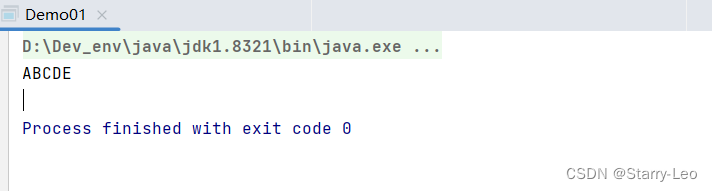
演示结果：

求X^n问题

比如: 2^10 2的10次幂
采用分治法
2^10拆成

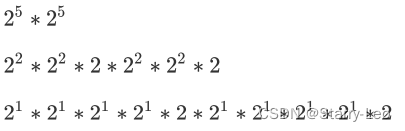
代码实现：

package com.xxliao.algorithms.divide_conquer;

/**
 * @author xxliao
 * @description: 比如: 2^10 2的10次幂
 * 采用分治法
 * @date 2024/5/31 21:44
 */

public class Demo02 {

    public static void main(String[] args) {
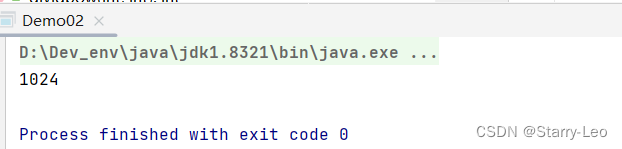
        System.out.println( dividpow(2,10) ); 
    }

    public static int dividpow(int x,int n){
        //递归结束 任何数的1次方都是它本身
        if(n==1){
            return x;
        }
        //每次分拆成幂的一半
        int half=dividpow(x,n/2);
        //偶数
        if(n%2==0){
            return half*half;
        }
        else{
            return half*half*x;
        }
    }
}

演示结果：