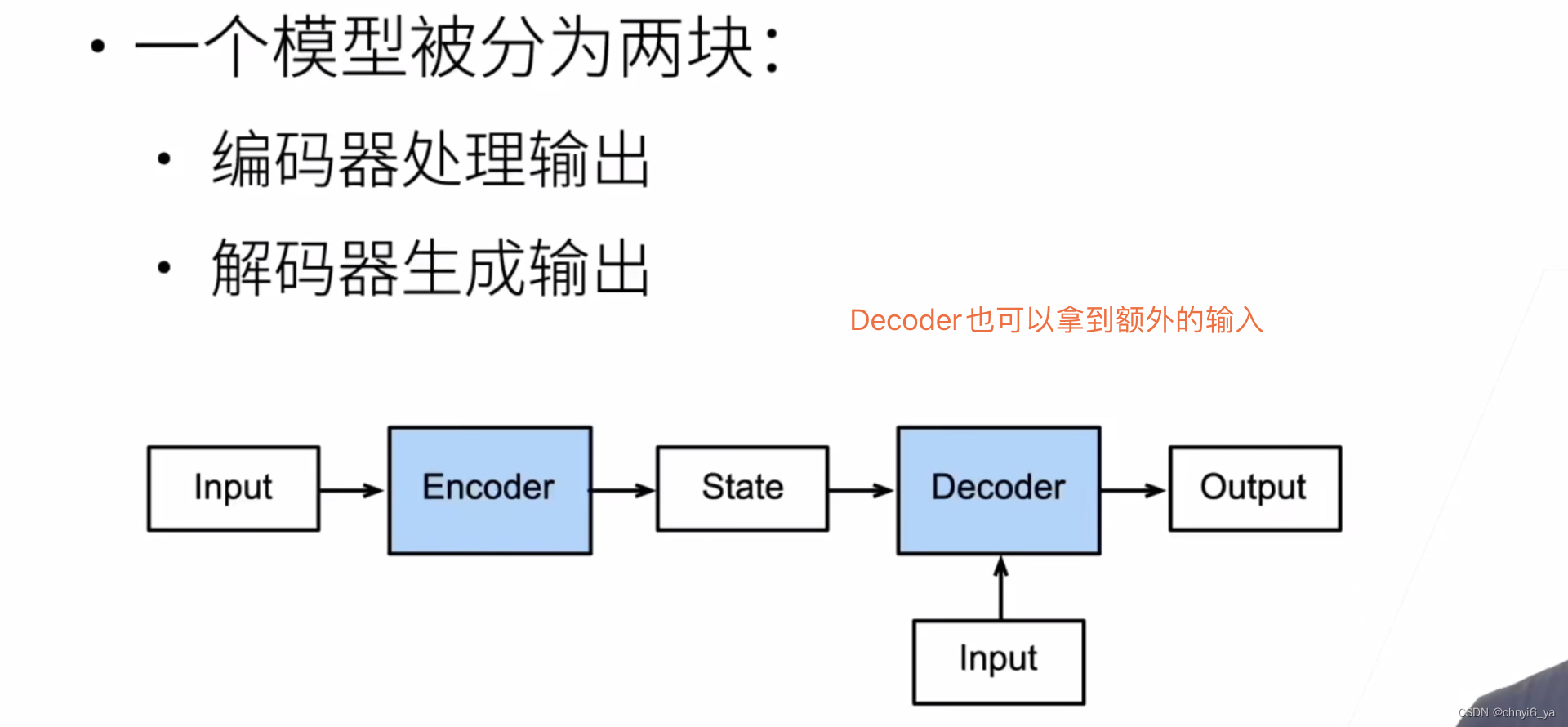
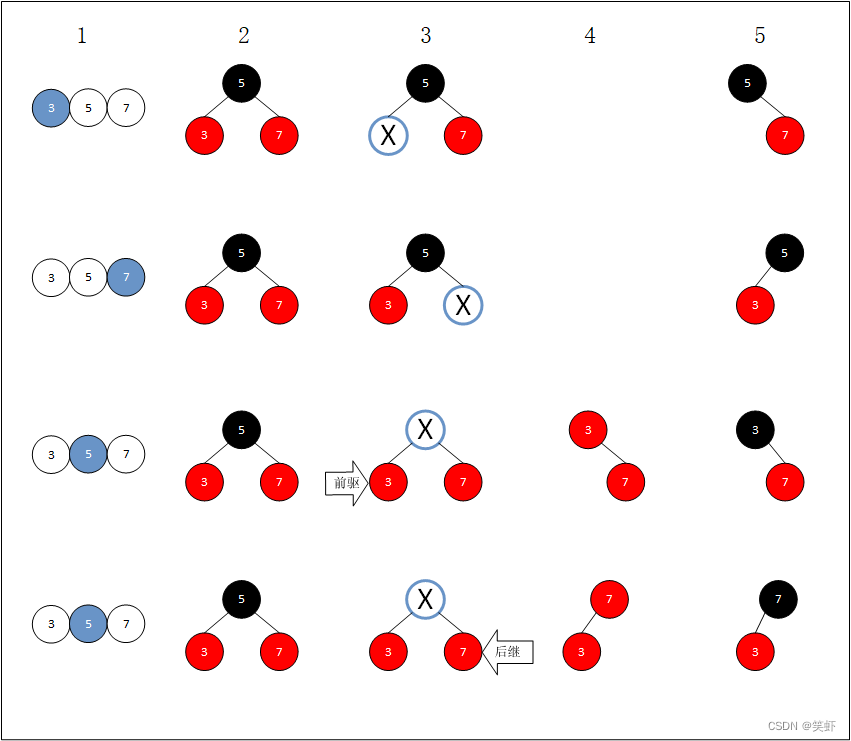
空间滤波概念

1. 滤波：通过修改或者抑制给定图像的特定频率分量，常见有低通滤波器与高通滤波器。
2. 空间滤波：将像素值使用该像素值及其邻域的值进行替换，替换方式有线性与非线性两种，即线性滤波器与非线性滤波器。

线性滤波器

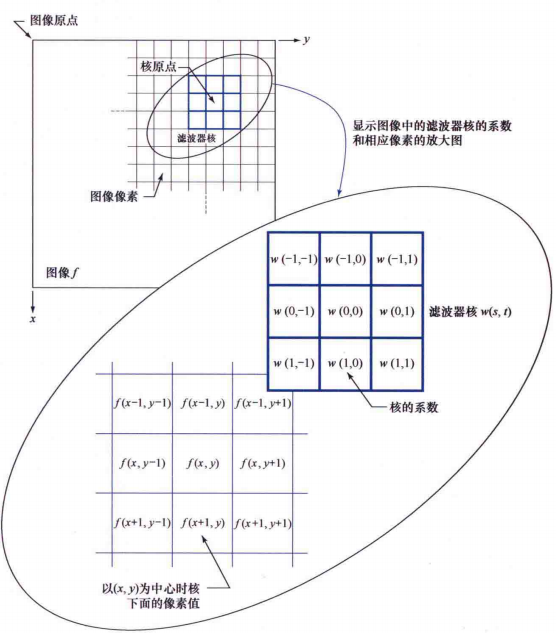
一般方式为是使用一个矩阵（也成为核）与图像进行类似卷积运算，做乘积。
矩阵内部的数值决定了滤波器的功能。

（下图来自数字图像处理 第4版=DIGITAL IMAGE PROCESSING,FOURTH EDITION）

可分离滤波器核

将二维矩阵分解为两个一维向量的乘积。
$G(X,Y)=G_1(X)G_2(Y)$
如
$$w=\begin{array}{c}\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]\end{array}$$
可表示为
$$w_1=\begin{array}{c}\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]\end{array}{w}_2=\begin{array}{c}\left[\begin{array}{ccc}1& 1& 1\end{array}\right]\end{array}$$
两者乘积。

PS:判断一个核是否是可分离卷积核，即判断该卷积核是否是秩为1.若为1，即可分离，否则不可。

卷积可分离的好处：
假设图像大小为$M\ast N$,卷积核大小为$m\ast n$,直接做卷积的运算量包括$MNmn$次乘法和$MNmn$次加法。若使用可分离卷积，将$w$分为$w_1\ast w_2$，并且$w_1$为$m\ast 1$，$w_2$为$1\ast n$,将图像矩阵与$w_1$和$w_2$分别做卷积得到运算量为$MNm+MNn$，即$MN(m+n)$。相比于之前的$MNmn$,大大减少了运算量。

可分离向量的确定：
根据矩阵的性质可知，秩为1的矩阵，每行之间只差常数倍，每列之间也只差常数倍，那么我们可以任意找一个行与列进行求解，当然需要保证该行与列都非零向量。

滤波器类型

线性滤波器

1. 低通空间滤波器
   \hspace{0.5cm} 主要作用于变化缓慢的区域，如光滑地面等；桌子边缘等为高频区域。
   1.1 盒式滤波器核
   \hspace{0.5cm} 该滤波器核的数值均为1,可使图片产生平滑效果。
   1.2 低通高斯滤波器核
   \hspace{0.5cm} 高斯核$w(s,t)=G(s,t)=K{e}^{-\frac{s^2+t^2}{2{\sigma }^2}}$
   \hspace{0.5cm} 其中$s$与$t$为到坐标（以核心为原点）,$(s^2+t^2{)}^{\frac{1}{2}}$为到原心的距离。
   
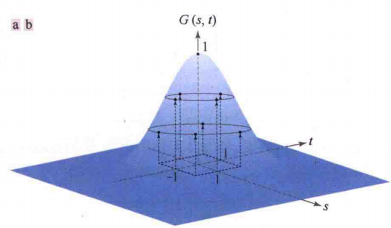
   特别地，高斯核也是可分离的。

2. 高通滤波器
   \hspace{0.5cm} 通过边缘增强等方式作用于图像。

非线性滤波器

1. 中值滤波
   \hspace{0.3cm} 将某像素及其邻域内的像素进行排序，中心像素的值由邻域内的像素排序的中间值确定，尤其对椒盐噪声有消除作用。
2. 最大值滤波器和最小值滤波器
   \hspace{0.3cm} 最大值滤波器：将某像素及其邻域内的像素进行排序，中心像素的值由邻域内的像素排序最大值确定。
   \hspace{0.3cm} 最小值滤波器：将某像素及其邻域内的像素进行排序，中心像素的值由邻域内的像素排序最大值确定。
3. 中点滤波器
   \hspace{0.3cm} 将某像素及其邻域内的像素进行排序，中心像素值由最大值与最小值的平均值确定，适用于处理随机分布的噪声，如高斯噪声或者均匀噪声。
4. 修正$Alpha$均值滤波器
   \hspace{0.3cm} 对中值滤波器的改进，将某像素及其邻域内的像素删除部分最低灰度值与最高灰度值，剩下的像素值进行计算算术平均值，作为中心像素值，适用于处理混合噪声，如椒盐噪声与高斯噪声的混合。

自适应滤波器

自适应重在考虑图像的不同特征点变化。

1. 自适应局部降噪滤波器
   \hspace{0.3cm} 该滤波器需要考虑的参数涉及带有噪声的图像像素值与噪声方差；滤波器中局部像素均值与局部方差。
   带有噪声的图像像素值为$f(x,y)$、噪声方差为${\sigma }_f$、局部均值为$\widehat{f_{xy}}$、局部方差为${\sigma }_{xy}$
   四个参数的计算方式可由直方图得出频率与相关值乘积得到。
   自适应的表达式为$\bar{f}(x,y)=f(x,y)-\frac{{\sigma }_f^2}{{\sigma }_{xy}^2}[f(x,y)-\widehat{f_{xy}}]$
   该式子的特点在于
   \hspace{0.6cm} 若噪声的方差为0，则滤波的结果为$f(x,y)$；
   \hspace{0.6cm} 若噪声的方差与局部方差相等，则滤波的结果为图像局部像素值的均值；
2. 自适应中值滤波器
   \hspace{0.3cm} 对中值滤波的优化
   在保留图像细节的同时平滑非冲激噪声（非变化剧烈）
   与自适应局部降噪滤波器类似，在局部区域进行计算。
   在局部区域中，$z_{min}$表示最小灰度值，$z_{max}$表示最大灰度值，$z_{med}$表示灰度值中值，$z_{xy}$为坐标$(x,y)$处的灰度值，$S_{max}$表示局部区域的大小。
   算法步骤：
   1. 若$z_{min}$ <$z_{med}$<$z_{max}$,则转到第二步；否则，增加局部区域大小，若局部区域大小小于$S_{max}$，重复步骤1，否则输出$z_{med}$
   2. 若$z_{min}$ <$z_{xy}$<$z_{max}$,则输出$z_{xy}$，否则输出$z_{med}$
      算法的主要思想在于通过两层判断，旨在消除冲激噪声，如在第一步转到第二步，可以保证$z_{med}$为非冲激噪声；第二步中无论输出$z_{med}$还是$z_{xy}$都达到了消除冲激噪声的目的。但如果最终在第一步中进行了输出，那么不能保证$z_{med}$是否为冲激噪声。
      PS:所以该算法旨在尽力消除，不保证全部消除。