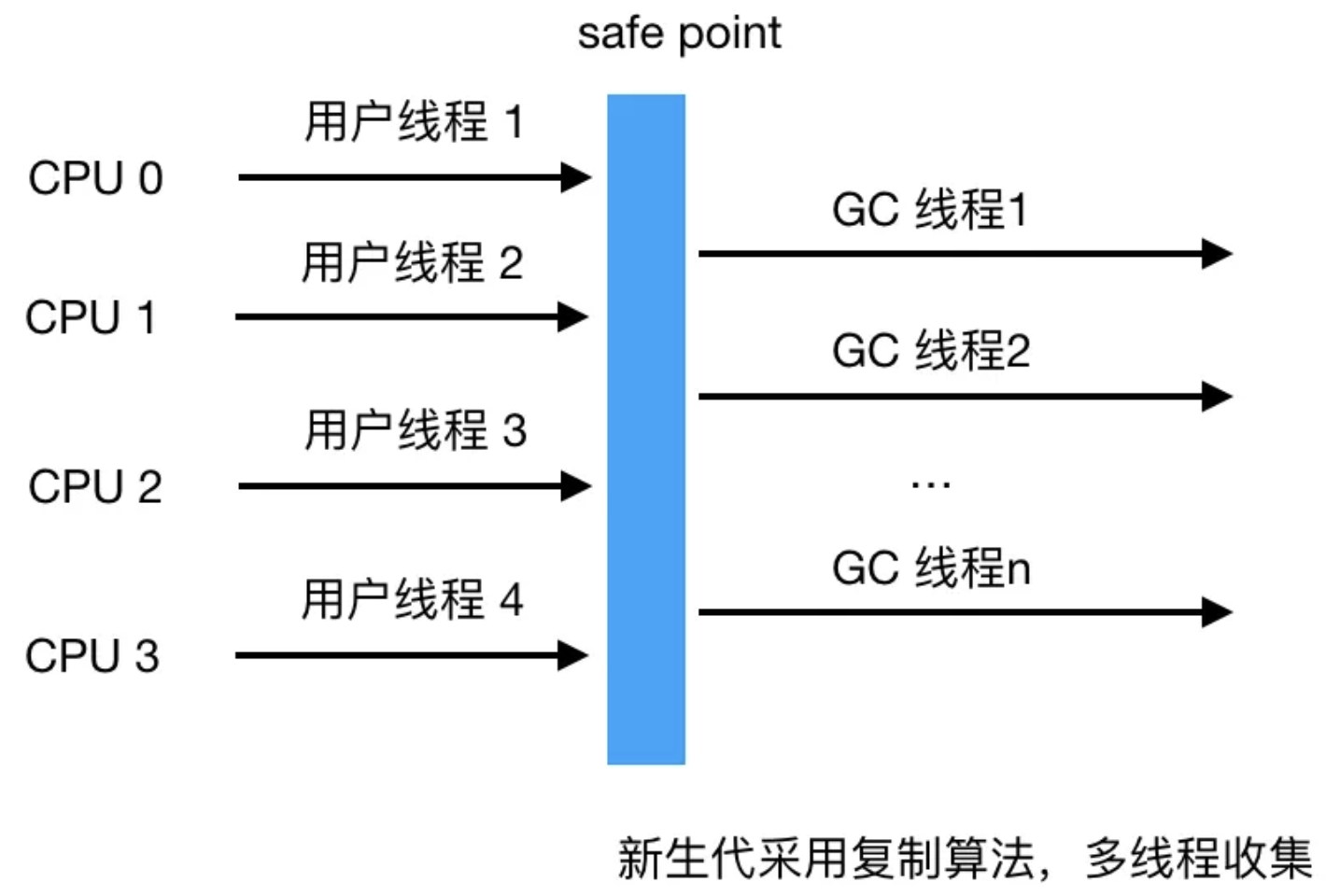
1. 快速排序的非递归版本

🆒🐧关键思路：
🍎① 参数中的begin和end来界定，是随着函数的调用自动保存在栈帧中的，而我们需要用栈这种数据结构来模拟这个过程。

🍎② 如果决定先排 keyi左边的元素的话，就要先把 keyi右边的元素先入栈(因为栈是后进先出的)

🍎③ 每次取两个元素，分别表示待排序区间下标的 起点和终点。

🍎④ if (left < keyi - 1)，if (keyi + 1 < right)因为要保证遍历的区间是有效的，所以需要这两个判断。

• 先把 key 左边的区间都按照规律入栈然后排序，只有把 key左边的都排好序之后，才会开始走 key右边的逻辑
  

// 快速排序的非递归法
void QuickSortNonR(int* a, int begin, int end)
{
	ST s;
	STInit(&s);
	STPush(&s, end);
	STPush(&s, begin);

	while (!STEmpty(&s))
	{
		int left = STTop(&s);
		STPop(&s);
		int right = STTop(&s);
		STPop(&s);

		int keyi = PartSort3(a, left, right);
		
		// [left, keyi-1] keyi [keyi+1, right]
		if (left < keyi - 1)
		{
			STPush(&s, keyi - 1);
			STPush(&s, left);
		}

		if (keyi + 1 < right)
		{
			STPush(&s, right);
			STPush(&s, keyi + 1);
		}
	}
	STDestroy(&s);
}

---

2. 快速排序

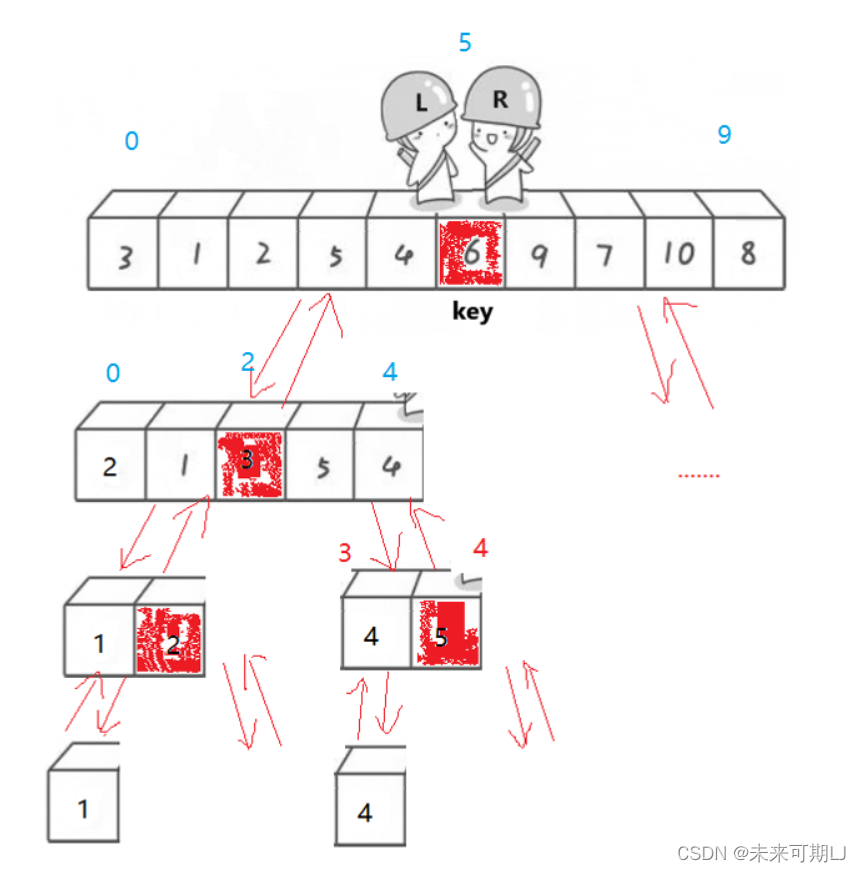
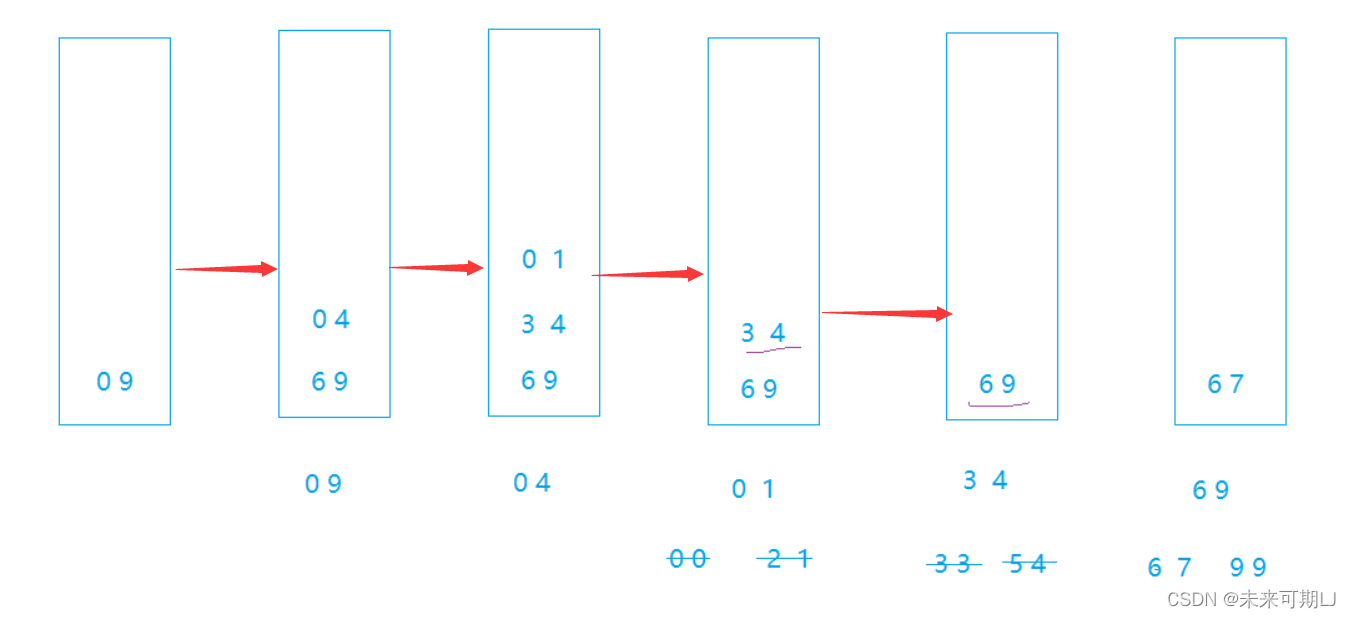
• 🍎基本思想：
• 任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

---

• 🆒快速排序有三个版本：

2.1 hoare 版本一

int PartSort1(int* a, int begin, int end)
{
	int midi = GetMidi(a, begin, end);
	Swap(&a[midi], &a[begin]);

	int left = begin, right = end;
	int keyi = begin;

	while (left < right)
	{
		// 右边找小
		while (left < right && a[right] >= a[keyi])
		{
			--right;
		}

		// 左边找大
		while (left < right && a[left] <= a[keyi])
		{
			++left;
		}

		Swap(&a[left], &a[right]);
	}

	Swap(&a[left], &a[keyi]);

	return left;
}

---

2.2 挖坑法 🐧版本二

int PartSort2(int* a, int begin, int end)
{
	int midi = GetMidi(a, begin, end);
	Swap(&a[midi], &a[begin]);

	int key = a[begin];
	int hole = begin;
	while (begin < end)
	{
		// 右边找小，填到左边的坑
		while (begin < end && a[end] >= key)
		{
			--end;
		}

		a[hole] = a[end];
		hole = end;

		// 左边找大，填到右边的坑
		while (begin < end && a[begin] <= key)
		{
			++begin;
		}

		a[hole] = a[begin];
		hole = begin;
	}

	a[hole] = key;
	return hole;
}

---

2.3 前后指针 版本三

int PartSort3(int* a, int begin, int end)
{
	int midi = GetMidi(a, begin, end);
	Swap(&a[midi], &a[begin]);
	int keyi = begin;

	int prev = begin;
	int cur = prev + 1;
	while (cur <= end)
	{
		if (a[cur] < a[keyi] && ++prev != cur)
			Swap(&a[prev], &a[cur]);

		++cur;
	}

	Swap(&a[prev], &a[keyi]);
	keyi = prev;
	return keyi;
}

2.4 调用以上的三个版本的快排

// [begin, end]
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;

	int keyi = PartSort2(a, begin, end);	// 此处修改需要调用的版本
	
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi+1, end);
}

---

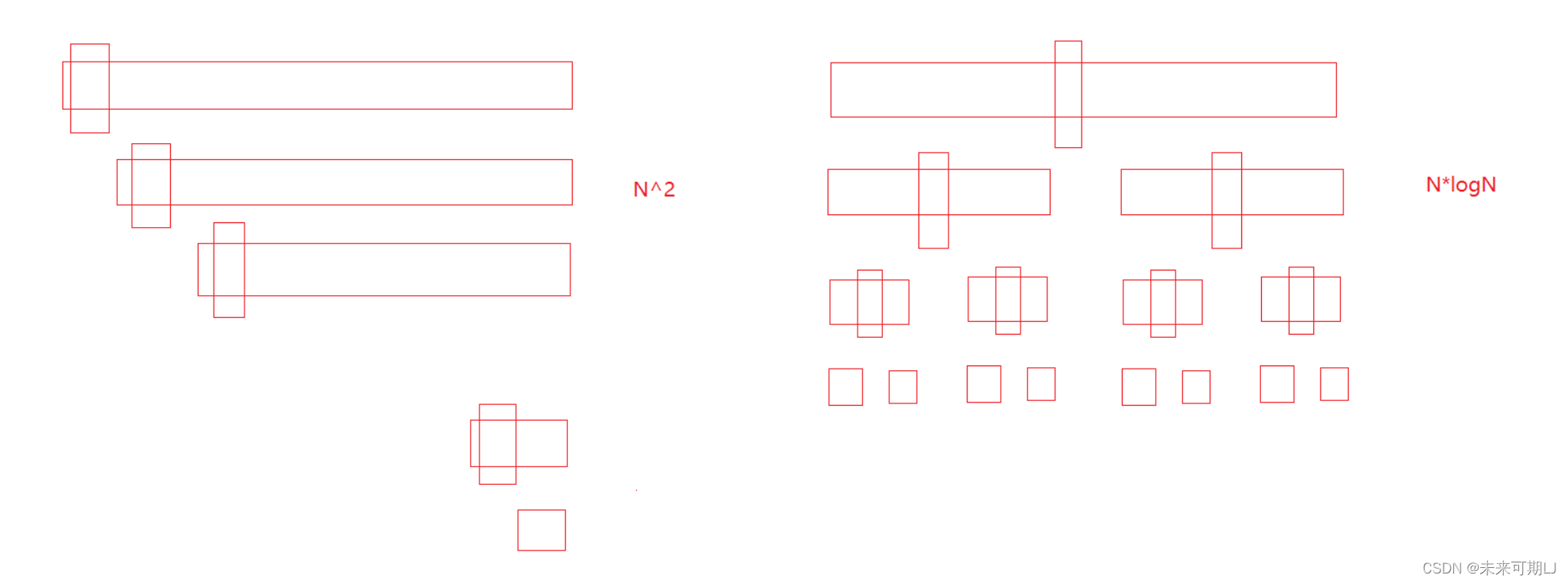
3. 快速排序的优化

• 🍎① 三数取中法选 key
  如果不采取三数取中的方法，万一每次快排的 key都是待排序中的最大值，此时每次只能将一个数据变成有序，此时的效率极低，所以需要优化。
  

int GetMidi(int* a, int begin, int end)
{
	int midi = (begin + end) / 2;
	// begin midi end 三个数选中位数
	if (a[begin] < a[midi])
	{
		if (a[midi] < a[end])
			return midi;
		else if (a[begin] > a[end])
			return begin;
		else
			return end;
	}
	else // a[begin] > a[midi]
	{
		if (a[midi] > a[end])
			return midi;
		else if (a[begin] < a[end])
			return begin;
		else
			return end;
	}
}

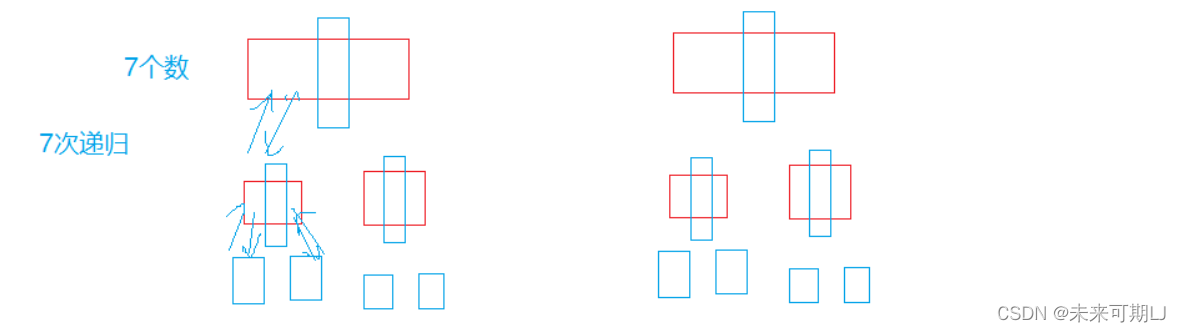
• 🍎② 递归到小的子区间时，可以考虑使用插入排序.
  当小区间的时候，因为用递归的话，会消耗更多的资源，效率较低。
  

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)		return;

	if (end - begin + 1 <= 10)
	{
		InsertSort(a + begin, end - begin + 1);
	}
	else
	{
		int midi = GetMidi(a, begin, end);
		Swap(&a[midi], &a[begin]);

		int left = begin, right = end;
		int keyi = begin;

		while (left < right)
		{
			// 右边找小
			while (left < right && a[right] >= a[keyi])
			{
				--right;
			}

			// 左边找大
			while (left < right && a[left] <= a[keyi])
			{
				++left;
			}

			Swap(&a[left], &a[right]);
		}

		Swap(&a[left], &a[keyi]);
		keyi = left;

		// [begin, keyi-1] keyi [keyi+1, end]
		QuickSort(a, begin, keyi - 1);
		QuickSort(a, keyi + 1, end);
	}
}