这是一道 中等难度 的题，是 判断链表是否有环 的扩展，在有环的情况下返回入环节点， 依然是两种解法。题目来自：leetcode

题目

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。
不允许修改 链表。

示例 1：

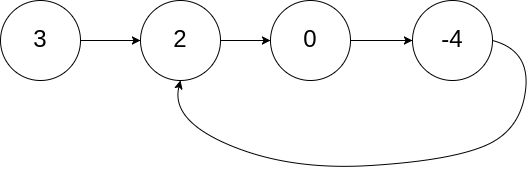
输入：head = [3,2,0,-4], pos = 1 
输出：返回索引为 1 的链表节点 
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

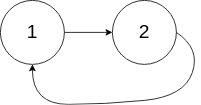
输入：head = [1,2], pos = 0 
输出：返回索引为 0 的链表节点 
解释：链表中有一个环，其尾部连接到第一个节点。 

示例 3：

输入：head = [1], pos = -1 
输出：返回 null 
解释：链表中没有环。 

提示：
● 链表中节点的数目范围在范围 $[0,10^4]$ 内
● $-10^5<=Node.val<=105^5$
● pos 的值为 -1 或者链表中的一个有效索引

进阶： 你是否可以使用 $O(1)$ 空间解决此题？

解法一：循环标记

循环遍历每一个节点并标记为已访问，返回第一次遍历到的已访问节点，否则最后返回 null 。

Java代码实现

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
 
        Set<ListNode> visited = new HashSet<>();
        while(head != null){
            if(visited.contains(head)){
                return head;
            }
            visited.add(head);
            head = head.next;
        }
        return null;

    }
}

Go 代码实现

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func detectCycle(head *ListNode) *ListNode {

    visited := make(map[*ListNode]bool)
    for head != nil {
        if visited[head]{
            return head;
        }
        visited[head] = true
        head = head.Next
    }
    return nil

}

复杂度分析

时间复杂度 $O(N)$：需要访问链表中的每一个节点，时间复杂度为链表长度n。
空间复杂度 $O(N)$：需要记录每个访问过的节点，空间复杂度为链表的长度n。

解法二：快慢指针

快指针每次走 2 步， 慢指针每次走 1 步，若 快慢指针 能够相遇说明链表有环，但是第一次相遇的点并不一定是入环点，如下所示：

相遇点 7 并不是入口点 4 。

那么怎么找到入环点呢？假如入环点前有 a 个节点，环上有 b 个节点，第一次相遇时快指针走了 f 步，慢指针走了 s 步。

由以上假设可以得知：

1. f = 2s；（快指针走的步数是慢指针的 2 倍）
2. f - s = nb；（快指针比慢指针多走了 n 个环的步数，然后相遇）
   即第一次相遇时，慢指针走了 nb 步，快指针走了 2nb 步。

第一次相遇的点还需要走多少步到达入环点？

因为到达入环点的步数为：a + nb, 其中 n >= 0。现在 慢指针 已经走了 nb 步，那么再走 a 步必定可以到达入环点，但是我们并不知道 a 是多少。

我们可以换个思路，此时可以把 快指针 重新指到起始点 head，即 快慢指针 到达入环点为步数都是 a , 那么当 快慢指针 再次相遇的地方就是入环点了。

完整流程如下：

Java 代码实现

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {

        ListNode fast = head, slow = head;
        while(fast != null && fast.next != null){
            fast = fast.next.next;
            slow = slow.next;
            // 第一次相遇
            if(slow == fast){
                fast = head;
                while(fast != slow){
                    fast = fast.next;
                    slow = slow.next;
                }
                // 第二次相遇
                return fast;
            } 
            
        }
        return null;
        
    }
}

Go 代码实现

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func detectCycle(head *ListNode) *ListNode {

    fast, slow := head, head
    for fast != nil && fast.Next != nil {
        fast, slow = fast.Next.Next, slow.Next
        if(slow == fast){
            fast = head
            for fast != slow {
                fast, slow = fast.Next, slow.Next
            }
            return fast
        }
    }
    return nil

}

复杂度分析

时间复杂度 $O(N)$：时间复杂度为慢指针所走的步数为 nb + a -> (n - 1)b + (a + b) -> (n - 1)b + 链表的总节点数 ，因为 n 和 b 都是是常数，所以复杂度近似为 $O(N)$。
空间复杂度 $O(1)$：只需要记录快慢指针的位置，为常数空间复杂度。