1. 动态规划问题的本质

• 记忆化地暴力搜索所有可能性来得到问题的解

我们常常会遇到一些问题，需要我们在n次操作，且每次操作有k种选择时，求出最终需要的最小或最大代价。处理类似的问题，我们一般需要遍历所有的可能性(相当于走一遍所有的路径)，然后找到我们所需要的解。
很明显我们可以构成一棵“决策树”，假设n=2,k=3,那么：

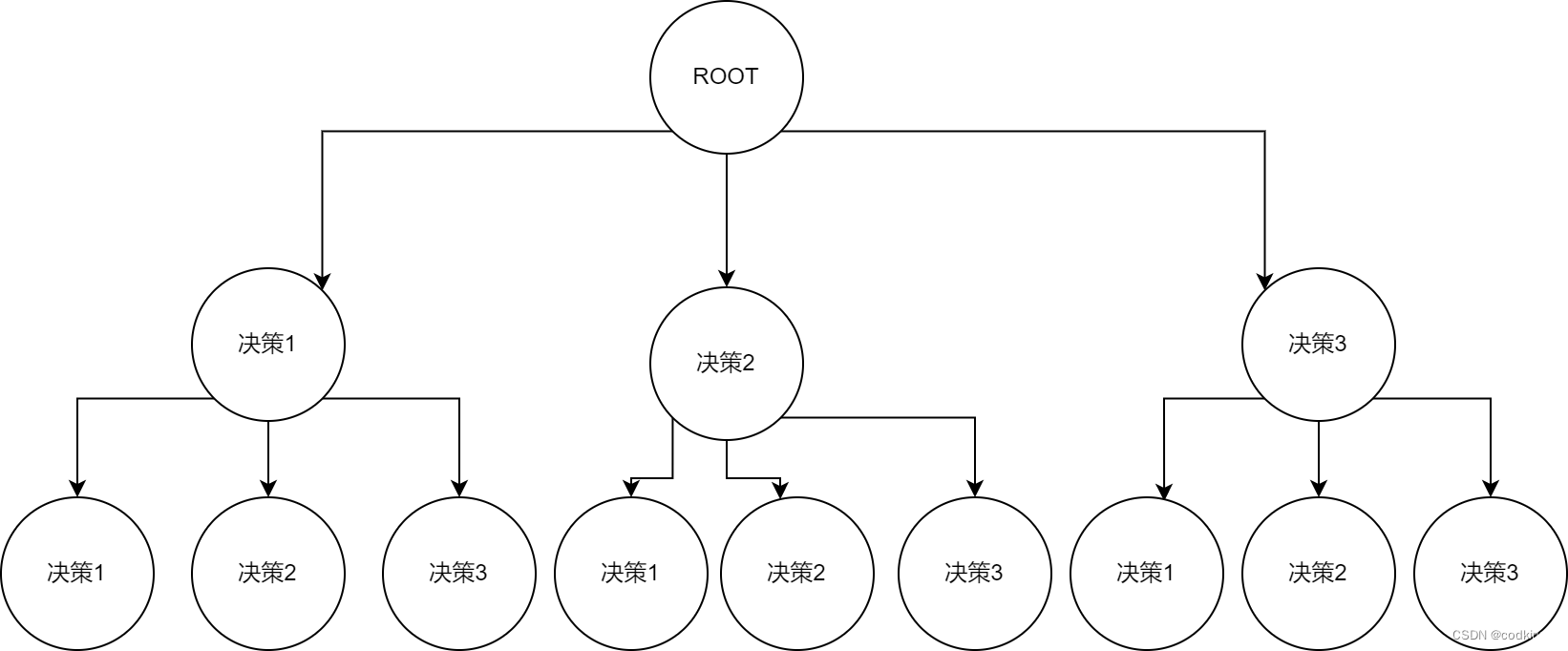
我们可以通过DFS或者BFS来遍历整棵树，从而搜寻到我们需要的结果。
时间复杂度：O(k^n)

但是我们可以看到，时间复杂度是指数级别的，一旦n的数级够大，那么时间代价是极大的。

这个时候，我们就需要用到动态规划的思想了。我们可以发现，执行决策的时候，经常会出现重复决策的地方，在第一次操作的时候有三种决策，在第二次操作时，在执行了决策1的情况下，又执行了三次相同的决策。这些重复的路径所导致的结果是相同的，那么我们完全可以直接调用之前的结果，大大减少了时间代价。
那么我们是否可以将遍历过的路径保存在一个数组(容器)中，如果我们遇到了重复的路径，直接访问之前访问过的路径的结果，并将其转移过来到当前的位置。

所以其本质上还是暴力搜索了所有可能，只不过加上了记忆曾经遍历过的路径

2. 01背包问题

01背包问题是主要解决n个物品的放置问题，对于物品的放与不放，如果放的话改怎么放的决策进行搜索。
下面会根据一道蓝桥杯的典型例题来辅助讲解01背包及其空间压缩的问题。

题目链接：

https://www.luogu.com.cn/problem/P8742

题面描述

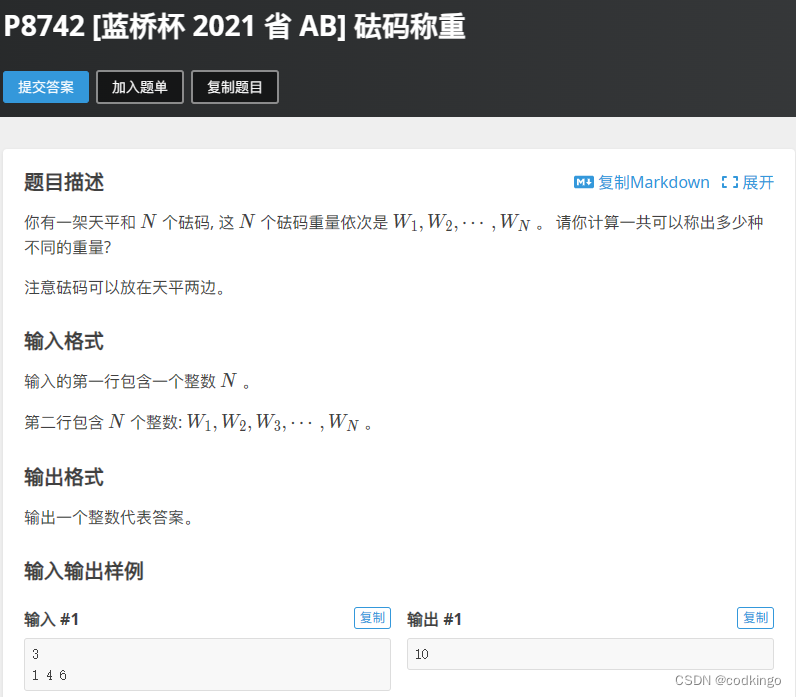
思路分析

• 显而易见，每个砝码的放置有三种情况：1.放左边 2.放右边 3.不放。如果使用DFS遍历所有情况，那么时间复杂度为3^n，n的取值可以到100，必然超时。
• 假设当我们放完第一个物品时，我们开始放第二个物品，我们可以单独放；可以放在第一个物品的同侧，也可以放在第一个物品的异侧。后两种情况是建立在第一个物品放的情况下结果，所以我们很明显要知道是否存在物品一放了的重量是否存在。
• 我们定义dp[i][j]的含义是之考虑前i个物品放置的所有情况下，背包容量为j时，是否存在
  这样的物品放置的情况刚好装满。
• 则状态转移方程为：
  1.当不放第i个物品时: dp[i][j]=dp[i-1][j]
  2.当只有第i个物品,即如果j==a[i]：dp[i][j]=1
  3.当减少第i个物品,即如果dp[i-1][j+a[i]]==1：dp[i][j]=1
  4.当增加第第i个物品，即如果dp[i-1][|j-a[i]|==1：dp[i][j]=1
• 我们来分析一下状态转移方程：
  因为我们有三种决策：1.放左边 2.放右边 3.不放。

1. 不放物品就不必说了，直接转移保存上次的状态即可。其次，我们可以单独放一个物品，所以有了方程2；然后是在放前i-1的物品的情况下，将第i个物品放在左侧或右侧。
2. 假设我们以左侧的重量来遍历j，那么放在左侧就是加上这个砝码，那么就需要记忆化查询没有加上这个砝码时的重量是否存在，若存在，那么j可以称出，否则不能；放在右侧也是同理。

下面是AC代码

#include "bits/stdc++.h"
using namespace std;
#define int long long
#define endl '\n'
const int MAXN=105;
const int MAXM=1e5+10;
int n;
int a[MAXN];
int dp[MAXN][MAXM];
void solve() {
    cin >> n;
    int s=0;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        s+=a[i];
    }

    dp[0][0] = 1;
    for (int i = 1; i <= n; ++i) {
        for (int j = 0; j <= s; ++j) {
            dp[i][j] = dp[i-1][j];
            if (j == a[i]) dp[i][j] = 1;
            if (j+a[i] <= s && dp[i-1][j+a[i]] == 1) dp[i][j] = 1;
            if (dp[i-1][abs(j-a[i])] == 1) dp[i][j] = 1;
        }
    }
    int ans=0;
    for (int j = 1; j <= s; ++j) {
        if (dp[n][j] == 1) ans++;
    }
    cout << ans << endl;
}

signed main() {
    ios :: sync_with_stdio(false);
    cin.tie(nullptr);
    int t=1;
    //cin >> t;
    while (t--) solve();
}

3. 如何进行空间压缩

我们可以发现，每次遍历到第i个砝码的时候，我们只会用到上一次(第i-1)时的状态，从0~i-2的空间不再被使用，那么我们完全可以将其压缩掉，达到优化空间复杂度的目的。

那么该如何进行空间压缩呢？

这里我们引入了滚动数组的概念，将dp数组想象成动态滚动更新的。可以视作将数组分为两部分：一部分是i-1状态下的数组；另一部分是i状态下的数组：

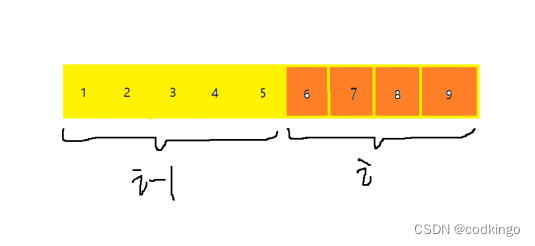
我们在增加第i个物品的时候，需要找到未考虑第i个物品时(i-1状态)且未增加第i个物品的重量(j-a[i])这个时候的状态，然后考虑进行状态转移。
假设如上图所示，我们现在遍历到重量为6的状态，那么6-a[i]的质量6的前面(保证a[i]范围的合理性)，而6的前面刚好都是i-1状态下的，并没有被更新。就这样一直滚动，知道数组全部被更新为i状态。
这也是为什么背包问题被压缩为一维后，需要逆序遍历背包容量的原因。那么同理，如果需要减少第i个物品，那么我们要拿到i-1下的状态，那就要顺序遍历。

压缩后的代码

#include "bits/stdc++.h"
using namespace std;
#define int long long
#define endl '\n'
const int MAXN=105;
const int MAXM=1e5+10;
int n;
int a[MAXN];
int dp[MAXM];
void solve() {
    cin >> n;
    int s=0;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        s+=a[i];
    }

    dp[0] = 1;


    for (int i = 1; i <= n; ++i) {
        for (int j = s; j >= a[i]; --j) {
            if (dp[j-a[i]] == 1) dp[j] = 1;
        }
    }

    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= s-a[i]; ++j) {
            if (dp[j+a[i]] == 1) dp[j] = 1;
        }
    }

    int ans=0;
    for (int j = 1; j <= s; ++j) {
        if (dp[j] == 1) ans++;
    }
    cout << ans << endl;
}

signed main() {
    ios :: sync_with_stdio(false);
    cin.tie(nullptr);
    int t=1;
    //cin >> t;
    while (t--) solve();
}

总结

• 总而言之，言而总之。动态规划问题的核心是利用空间换取时间，将曾经经过的状态保存下来，当在往后的遍历中如果需要该状态就不必再次重复一遍，只需直接访问当时的状态结果即可。
• 而滚动数组的用法很巧妙地将上一层地状态保存下来的同时完成了对当前状态的更新。
  希望此文章会对您对动态规划的学习有一定帮助~