【LeetCode】891.子序列宽度之和

news2025/7/26 7:55:37

**> ## 题目描述

一个序列的宽度定义为该序列中最大元素和最小元素的差值。
给你一个整数数组 nums ，返回 nums 的所有非空子序列的宽度之和。由于答案可能非常大，请返回对 10⁹ + 7 取余后的结果。
子序列定义为从一个数组里删除一些（或者不删除）元素，但不改变剩下元素的顺序得到的数组。例如，[3,6,2,7] 就是数组 [0,3,1,6,2,2,7] 的一个子序列。

示例 1：

输入：nums = [2,1,3]
输出：6
解释：子序列为 [1], [2], [3], [2,1], [2,3], [1,3], [2,1,3] 。
相应的宽度是 0, 0, 0, 1, 1, 2, 2 。
宽度之和是 6 。

示例 2：

输入：nums = [2]
输出：0

提示：

1 <= nums.length <= 105
1 <= nums[i] <= 105

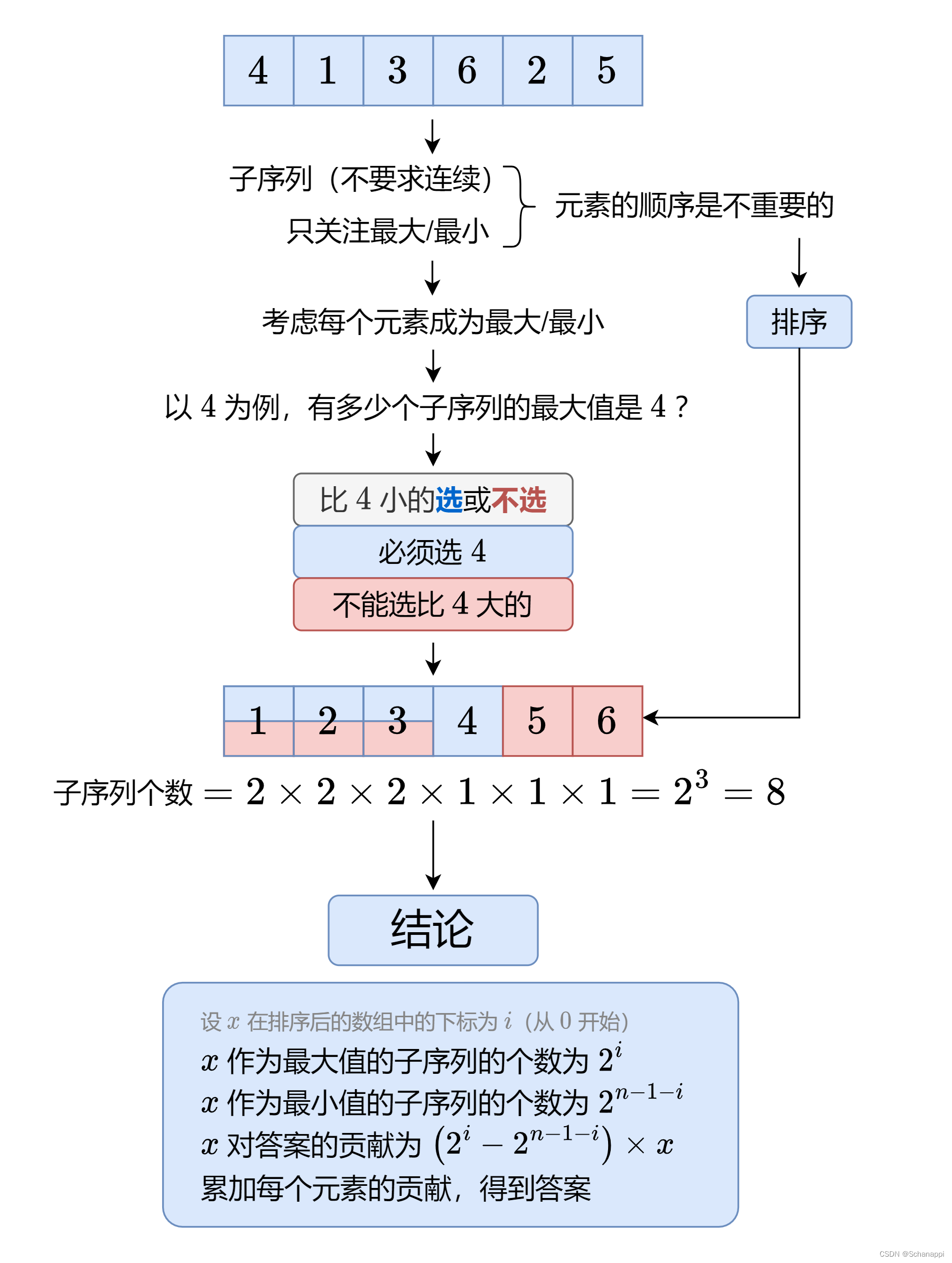
方法一：元素贡献度

class Solution {
public:
    const int MOD = 1e9+7;
    int sumSubseqWidths(vector<int>& nums) {
        // 排序
        sort(nums.begin(), nums.end());
        long sum=0;
        int n=nums.size(), pow2[n];
        pow2[0]=1;

        // 预先处理pow2 即二次幂
        for(int i=1; i<n; i++)  pow2[i] = pow2[i-1] * 2 % MOD;

        for(int i=0; i<n; i++){
            sum += long(pow2[i] - pow2[n- i -1]) * nums[i];
        }
        return (sum % MOD + MOD) % MOD;
    }
};

方法二：方法一 + 快速幂

class Solution {
public:
    const int MOD = 1e9+7;
    // 快速幂（迭代）
    long pow(long x, int n){
        long res = 1L;
        for(; n; n/=2){
            // n的最低位为1，需要计入贡献
            if(n % 2)   res = res * x % MOD;
            x = x * x % MOD;
        }
        return res;
    }
    int sumSubseqWidths(vector<int>& nums) {
        // 排序
        sort(nums.begin(), nums.end());
        long sum=0L;
        int n=nums.size();


        for(int i=0; i<n; i++){
            sum += (pow(2L, i) - pow(2L, n-1-i)) * nums[i];
        }
        return (sum % MOD + MOD) % MOD;
    }
};

心得

这道题本来打算自己做的，一开始还想到了set，但是对于单个元素的操作不方便，最后还是看了题解。

方法一：计算每个元素的贡献度
1.具体思路看图就很简单了，这里解释一下为什么最终的贡献是 (2ⁱ - 2^n-1-i) * x，对于元素x而言，作为最大值的时候需要减去最小值，那么在最终表达式展开的时候就有2ⁱ * x ，作为最小值的时候会被最大值减去，即-2^n-1-i * x，整合一下就得到 (2ⁱ - 2^n-1-i) * x 。
2.另外，通过排序可以快速得知nums[i]的大小顺序；
3.对于nums[i]的重复问题，无论是把nums[i]当作最大值还是最小值，组合数总取决于某一侧的个数，因此不会对正确答案产生影响。
4.对于2^k操作的重复问题，可以通过预先计算2的k次幂，之后之间查表获得。方法二会针对这个问题进行优化，即快速幂运算。