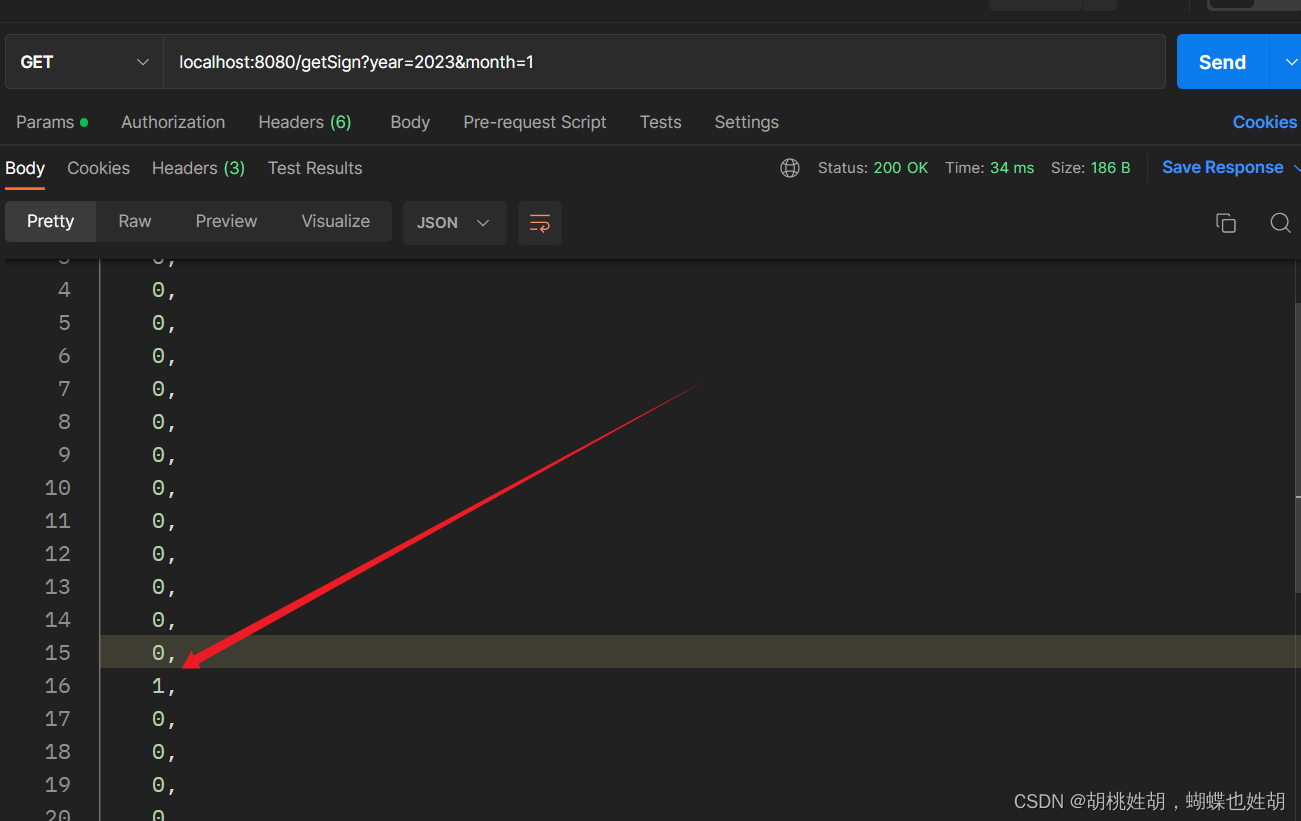
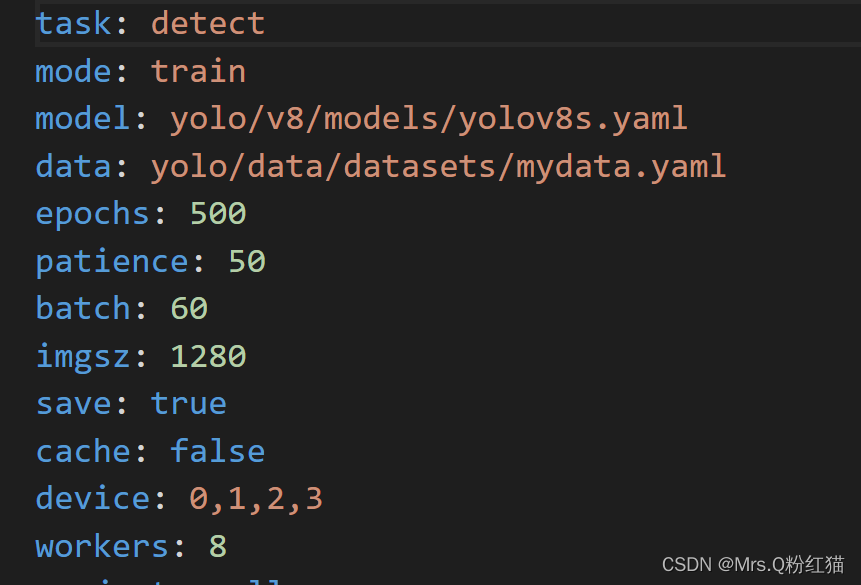
引言
最近刚看完贝塞尔曲线,工作就遇到了相应的需求,所以写一下过程。主要讲的是自动驾驶中,车换道时用到贝塞尔曲线,当然其他的很多领域也会有,例如图形学等。
在车遇到障碍物或者是前车速度较慢的时候,就会进入换道逻辑,那么如何从一个车道换到另外一个车道,同时要保证车里面的人的一个体感问题,就是如何平滑过度,这就是为什么要使用贝塞尔曲线来做换道时的轨迹生成了,OK那开始讲贝塞尔曲线了。
什么是贝塞尔曲线?
1. 一阶贝塞尔曲线:
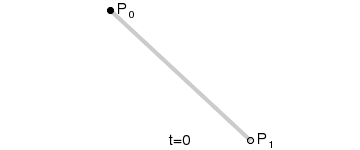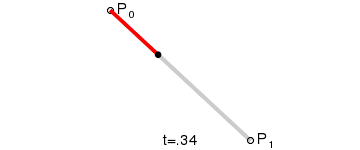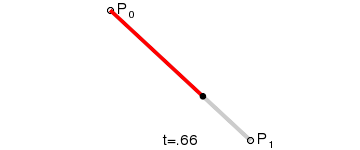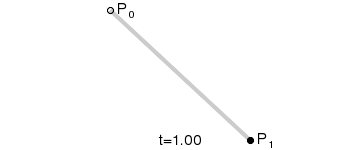
对于一阶贝塞尔曲线,从上图我们可以看到,它是一条直线,通过几何知识,很容易根据t 的值,得出线段上某个点的坐标:
B
1
(
t
)
=
P
0
+
(
P
1
−
P
0
)
t
B_{1}(t) = P_{0} + (P_{1}-P_{0})t
B1(t)=P0+(P1−P0)t
或者
B
1
(
t
)
=
(
1
−
t
)
P
0
+
P
1
t
,
0
<
t
<
1
B_{1}(t) = (1-t)P_{0} + P_{1}t , 0<t<1
B1(t)=(1−t)P0+P1t,0<t<1
一阶贝塞尔曲线, 就是根据t来的线性插值。P0和P1表示的是一个向量[ x , y ] , 其中x、y是分别按照这个公式来计算的。
2. 二阶贝塞尔曲线:
定义:起始点、终止点(也称锚点)、控制点。通过调整控制点,贝塞尔曲线的形状会发生变化。
- 由 P0 至 P1 的连续点 Q0,描述一条线段
- 由 P1 至 P2 的连续点 Q1,描述一条线段
- 由 Q0 至 Q1 的连续点 B(t),描述一条二次贝塞尔曲线
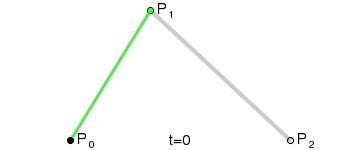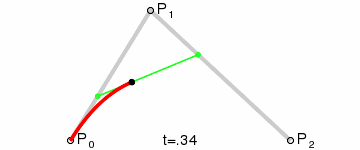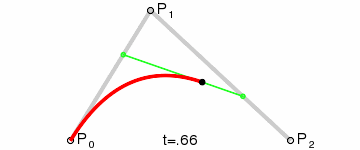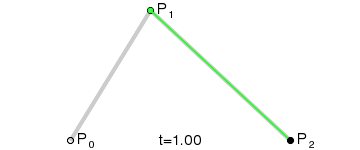
上面的红色曲线就是通过二阶公式生成的贝塞尔曲线(是不是很平滑🤗🤗🤗)。
下面是知乎大佬的原理讲解,比较好理解。
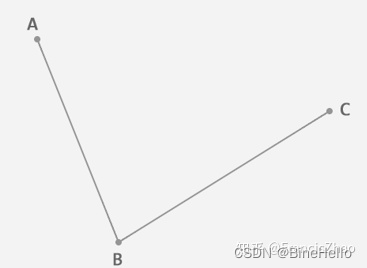
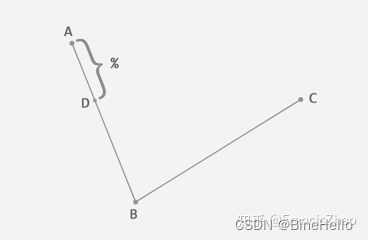
在平面内任选 3 个不共线的点,依次用线段连接。在第一条线段上任选一个点 D。计算该点到线段起点的距离 AD,与该线段总长 AB 的比例。
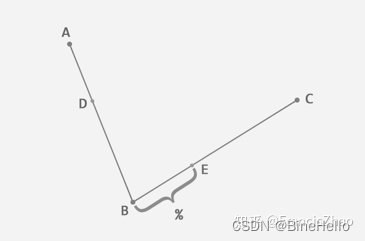
根据上一步得到的比例,从第二条线段上找出对应的点 E,使得 AD:AB = BE:BC。
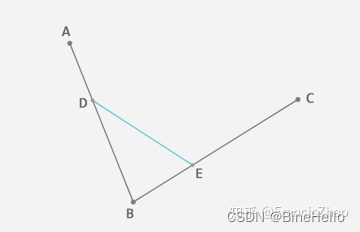
这时候DE又是一条直线了, 就可以按照一阶的贝塞尔方程来进行线性插值了, t= AD:AE
这时候就可以推出公式了

下面的P都是向量,如[x,y]。
P
0
′
(
t
)
=
(
1
−
t
)
P
0
+
P
1
t
,
0
<
t
<
1
P_{0}'(t) = (1-t)P_{0} + P_{1}t , 0<t<1
P0′(t)=(1−t)P0+P1t,0<t<1
<==>对应着上图绿色线段的左端点。
P
1
′
=
(
1
−
t
)
P
1
+
P
2
t
P_{1}' = (1-t)P_{1} + P_{2}t
P1′=(1−t)P1+P2t
<==>对应着上图绿色线段的右端点。
B
2
(
t
)
=
(
1
−
t
)
P
0
′
+
P
1
′
t
B_{2}(t) = (1-t)P_{0}' + P_{1}'t
B2(t)=(1−t)P0′+P1′t
=
(
1
−
t
)
(
(
1
−
t
)
P
0
+
t
P
1
)
+
t
(
(
1
−
t
)
P
1
+
t
P
2
)
= (1-t)((1-t)P_{0}+tP_{1})+t((1-t)P_{1}+tP_{2})
=(1−t)((1−t)P0+tP1)+t((1−t)P1+tP2)
=
(
1
−
t
)
2
P
0
+
2
t
(
1
−
t
)
P
1
+
t
2
P
2
= (1-t)^2P_{0}+2t(1-t)P_{1}+t^2P_{2}
=(1−t)2P0+2t(1−t)P1+t2P2
<==>对应着绿色线段的一阶贝塞尔曲线(线性插值)。
整理一下公式, 得到二阶贝塞尔公式:
B 2 ( t ) = ( 1 − t ) 2 P 0 + 2 t ( 1 − t ) P 1 + t 2 P 2 B_{2}(t) = (1-t)^2P_{0}+2t(1-t)P_{1}+t^2P_{2} B2(t)=(1−t)2P0+2t(1−t)P1+t2P2
3. 三阶贝塞尔曲线:
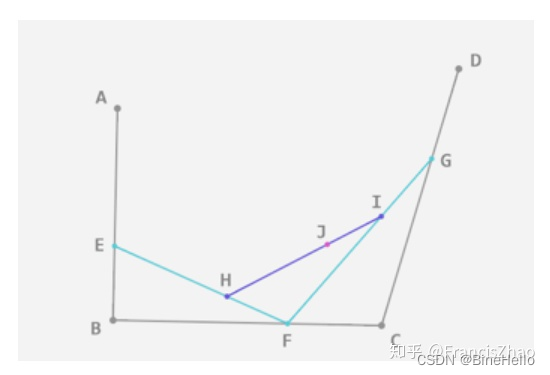
4. 高阶贝塞尔公式:
可以通过递归的方式来理解贝塞尔曲线, 但是还是给出公式才方便计算的。划重点了: 系数是二项式的展开. 后面的很多的贝塞尔曲线的性质都可以用这个来解释
P
(
t
)
=
∑
i
=
0
n
P
i
B
i
,
n
(
t
)
,
0
<
=
t
<
=
1
P_{}(t) = \sum_{i=0}^{n}P_{i}B_{i,n}(t),0<=t<=1
P(t)=i=0∑nPiBi,n(t),0<=t<=1
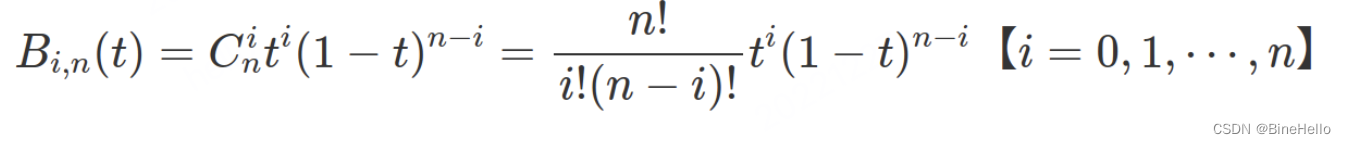
随着阶数的变化,图像中贝塞尔曲线也会跟着变化。
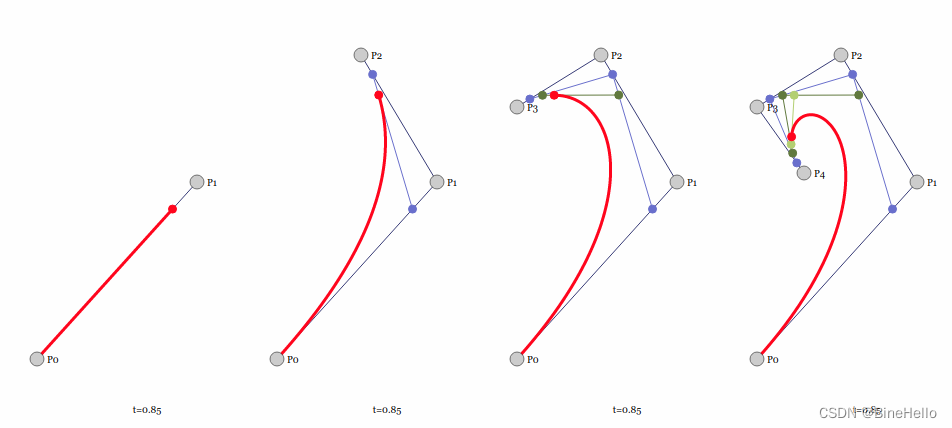
通过上面图,可以看出,最终的(红色)曲线,就是对这几个点进行拟合得到的贝塞尔曲线。
n个控制点对应着n-1 阶的贝塞尔曲线。
高阶的贝塞尔可以通过不停的递归直到一阶:
- 4次贝塞尔曲线需要【递归】用到3次贝塞尔曲线;
- 3次贝塞尔曲线需要【递归】用到2次贝塞尔曲线;
- 2次贝塞尔曲线需要【递归】用到1次贝塞尔曲线;
- 1次贝塞尔曲线就是线性插值,就是上面动图中的第一个图。
贝塞尔曲线的性质:
- 阶次是控制点个数减1。它限定了,给你n个点,你如果要使用贝塞尔曲线,那么只能使用n-1次贝塞尔曲线来拟合,这个限制条件不太友好;
- 牵一发动全身,移动一个控制点,整段曲线都会变化。
贝塞尔曲线的凸包性质
-
贝塞尔曲线始终会在包含了所有控制点的最小凸多边形中, 不是按照控制点的顺序围成的最小多边形。这点大家一定注意. 这一点的是很关键的,也就是说可以通过控制点的凸包来限制规划曲线的范围,在路径规划是很需要的一个性质.
-
凸包可以理解为,有一堆点集,使用一个橡皮筋来套住所有点,最后橡皮筋围成的形状,就是这些点集的凸包。上面最后一个图的5个点中,其实最后一个点P4不是在凸多边形上,而是在这些点组成的凸包内部。
-
用不严谨的话来讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边形,它能包含点集中所有的点。
贝塞尔曲线的生成
通过选取几个控制点来生成贝塞尔曲线,该曲线为自动驾驶车的参考线,车沿着轨迹走。
QT代码的实现:
//递归
double factorial(int n){
if(n<=1){
return 1;
}else {
return factorial(n-1)*n;
}
}
//贝塞尔公式
Vector2d bezierCommon(vector<Vector2d> Ps, double t){
if(Ps.size()==1){
return Ps[0];
}
Vector2d p_t(0.,0.);
int n = Ps.size()-1;
for (int i= 0; i< Ps.size(); i++) {
double C_n_i = factorial(n)/(factorial(i)*factorial(n-i));
p_t += C_n_i*pow((1-t),(n-i))*pow(t,i)*Ps[i];
}
return p_t;
}
//主函数调用
int MainWindow::bezier(){
vector<Vector2d>Ps{Vector2d (0,1),Vector2d(1,3),Vector2d(3,1),Vector2d(4,6),Vector2d(5,9)};
vector<double>x_ref,y_ref;
for(int i=0;i<Ps.size();i++){
x_ref.push_back(Ps[i][0]);
y_ref.push_back(Ps[i][1]);
}
for(int t=0;t<100;t++){
Vector2d pos = bezierCommon(Ps,(double)t/100);
x_.push_back(pos[0]);
y_.push_back(pos[1]);
return 0;
}
/****************************************************
*贝塞尔曲线画图
****************************************************/
int result = bezier();
QSplineSeries* series = new QSplineSeries(); // 创建一个样条曲线对象
QScatterSeries* seriesPoint = new QScatterSeries(); //散点
series->setName("曲线");
#if 1
// 添加生成的贝塞尔曲线的点
for (int var = 0; var < x_.size(); ++var) {
series->append(x_[var],y_[var]);
}
// 添加控制点
*seriesPoint << QPointF(0, 1)<< QPointF(1, 3)<< QPointF(3, 1)<< QPointF(4, 6)<<QPointF(5,9);
#else // 添加数据方式3,一次性更新所有数据
QList<QPointF> points;
for(int i = 0; i < 20; i++)
{
points.append(QPointF(i, i %7));
}
series->replace(points);
#endif
参考:
https://www.zhihu.com/question/29565629