学习目标：

DDPM

学习内容：

DDPM代码

学习时间：

11.13-11.18

学习产出：

一、DDPM

1、trainer

trainer用来计算损失，即将图片加噪后计算损失，损失公式如下：
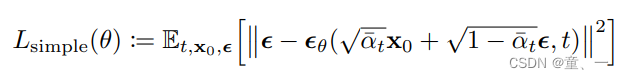
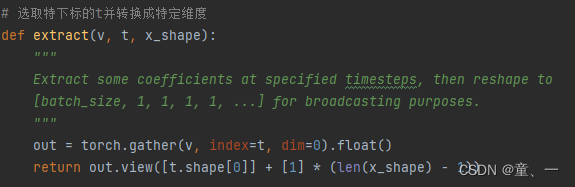
在这里插入图片描述

extract()函数：选取特下标的t并转换成特定维度

# 根据Loss公式计算Loss
class GaussianDiffusionTrainer(nn.Module):
    '''
    model=Unet，beta_1=β1，beta_T=βT，（β1，βT指方差的最小值和最大值，β1和βT产生linear schecule，越往后β越大，如果扩散步数T足够大，那么Xt忽悠完全丢掉了原始数据而变成了一个随机噪声），T指的是逆向计算中前向的时间步，
    '''

    def __init__(self, model, beta_1, beta_T, T):
        super().__init__()
        self.model = model
        self.T = T  # 1000
        # 得到一个线性增长的Bt
        self.register_buffer(
            'betas', torch.linspace(beta_1, beta_T, T).double())
        # 通过Bt得到论文中的α
        alphas = 1. - self.betas
        # 通过α累乘得到αt
        alphas_bar = torch.cumprod(alphas, dim=0)
        # calculations for diffusion q(x_t | x_{t-1}) and others
        self.register_buffer(
            'sqrt_alphas_bar', torch.sqrt(alphas_bar))
        self.register_buffer(
            'sqrt_one_minus_alphas_bar', torch.sqrt(1. - alphas_bar))
        print('计算loss')

    def forward(self, x_0):
        """
        Algorithm 1.
        随机生成t和噪声，通过t和噪声得到x_t(即通过t和噪声得到最终的噪声图像),计算出loss后返回
        """
        t = torch.randint(self.T, size=(x_0.shape[0],), device=x_0.device)  # torch.Size([64, 3, 32, 32])，生成的最大数为1000
        # 随机生成一个和X0一样的噪声
        noise = torch.randn_like(x_0)
        # 正向得到最终噪声图片Xt
        x_t = (
                extract(self.sqrt_alphas_bar, t, x_0.shape) * x_0 +
                extract(self.sqrt_one_minus_alphas_bar, t, x_0.shape) * noise)
        # 计算纯噪声noise和生成噪声Xt的loss
        loss = F.mse_loss(self.model(x_t, t), noise, reduction='none')
        return loss

forward()中
在这里插入图片描述
计算时间步

生成纯噪声noise

通过计算

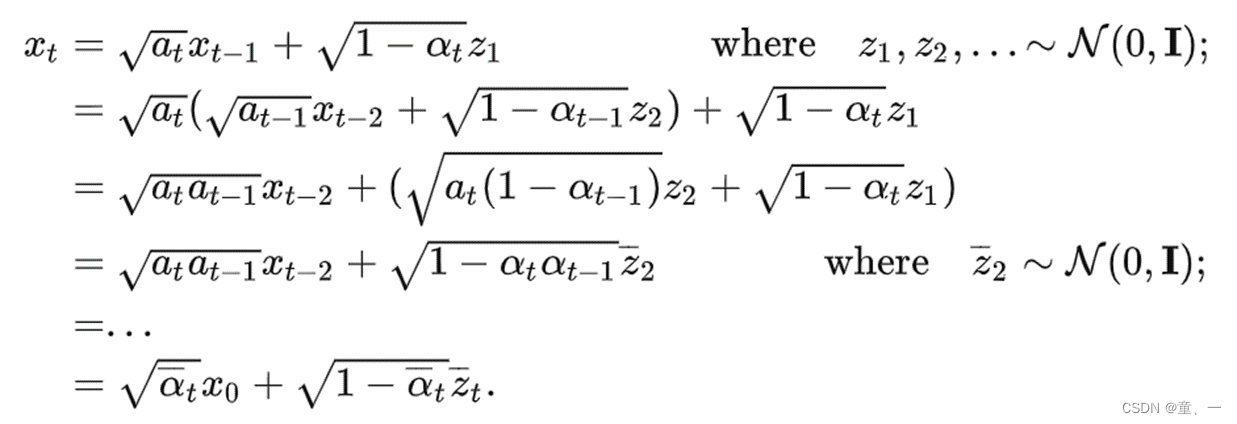
得到最终得噪声图片X_t。

然后通过

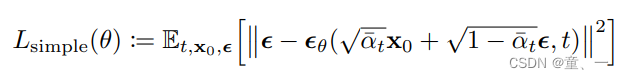
计算loss。计算loss伪代码为：

2、sampler

# 采样过程
class GaussianDiffusionSampler(nn.Module):
    '''
    mean_type表示均值采用的类型，var_type表示方差β固定很小或很大的值
    '''

    def __init__(self, model, beta_1, beta_T, T, img_size=32,
                 mean_type='eps', var_type='fixedlarge'):
        # xpre通过xt预测xt-1，xstart通过xt预测x0，epsilon为预测误差
        assert mean_type in ['xprev' 'xstart', 'epsilon']
        assert var_type in ['fixedlarge', 'fixedsmall']
        super().__init__()

        self.model = model
        self.T = T
        self.img_size = img_size
        self.mean_type = mean_type
        self.var_type = var_type
        self.register_buffer(
            'betas', torch.linspace(beta_1, beta_T, T).double())
        # 得到α
        alphas = 1. - self.betas
        # 得到αt
        alphas_bar = torch.cumprod(alphas, dim=0)
        # #所有alphas_bar向后移动一位，第一位等于1
        # 得到αt-1
        alphas_bar_prev = F.pad(alphas_bar, [1, 0], value=1)[:T]
        # calculations for diffusion q(x_t | x_{t-1}) and others
        self.register_buffer(
            'sqrt_recip_alphas_bar', torch.sqrt(1. / alphas_bar))
        self.register_buffer(
            'sqrt_recipm1_alphas_bar', torch.sqrt(1. / alphas_bar - 1))

        # calculations for posterior q(x_{t-1} | x_t, x_0)、
        # 方差
        self.register_buffer(
            'posterior_var',
            self.betas * (1. - alphas_bar_prev) / (1. - alphas_bar))
        # below: log calculation clipped because the posterior variance is 0 at
        # the beginning of the diffusion chain
        self.register_buffer(
            'posterior_log_var_clipped',
            torch.log(
                torch.cat([self.posterior_var[1:2], self.posterior_var[1:]])))
        # 均值公式中X0前面的常数
        self.register_buffer(
            'posterior_mean_coef1',
            torch.sqrt(alphas_bar_prev) * self.betas / (1. - alphas_bar))
        # 均值公式中Xt前面的常数
        self.register_buffer(
            'posterior_mean_coef2',
            torch.sqrt(alphas) * (1. - alphas_bar_prev) / (1. - alphas_bar))

    # 计算逆向过程需要的均值和方差
    def q_mean_variance(self, x_0, x_t, t):
        """
        Compute the mean and variance of the diffusion posterior
        q(x_{t-1} | x_t, x_0)
        """
        assert x_0.shape == x_t.shape
        # 通过均值公式的第一步乘以X0和第二步乘以Xt得到均值
        posterior_mean = (
                extract(self.posterior_mean_coef1, t, x_t.shape) * x_0 +
                extract(self.posterior_mean_coef2, t, x_t.shape) * x_t
        )
        # 得到方差
        posterior_log_var_clipped = extract(
            self.posterior_log_var_clipped, t, x_t.shape)
        return posterior_mean, posterior_log_var_clipped

    def predict_xstart_from_eps(self, x_t, t, eps):
        assert x_t.shape == eps.shape
        return (
                extract(self.sqrt_recip_alphas_bar, t, x_t.shape) * x_t -
                extract(self.sqrt_recipm1_alphas_bar, t, x_t.shape) * eps
        )

    def predict_xstart_from_xprev(self, x_t, t, xprev):
        assert x_t.shape == xprev.shape
        return (  # (xprev - coef2*x_t) / coef1
                extract(
                    1. / self.posterior_mean_coef1, t, x_t.shape) * xprev -
                extract(
                    self.posterior_mean_coef2 / self.posterior_mean_coef1, t,
                    x_t.shape) * x_t
        )

    # 计算逆向过程
    def p_mean_variance(self, x_t, t):
        # below: only log_variance is used in the KL computations
        # 后验分布方差
        model_log_var = {
            # for fixedlarge, we set the initial (log-)variance like so to
            # get a better decoder log likelihood
            'fixedlarge': torch.log(torch.cat([self.posterior_var[1:2],
                                               self.betas[1:]])),
            'fixedsmall': self.posterior_log_var_clipped,
        }[self.var_type]
        # print('model_log_var1',model_log_var)
        # 计算方差
        model_log_var = extract(model_log_var, t, x_t.shape)
        # print('model_log_var2',model_log_var)
        # Mean parameterization
        '''
        mean_type == 'xprev'和mean_type == 'xstart'没有使用，这里只用到第三种，即mean_type == 'epsilon'
        '''
        if self.mean_type == 'xprev':  # the model predicts x_{t-1}
            # print('xprev')
            x_prev = self.model(x_t, t)
            x_0 = self.predict_xstart_from_xprev(x_t, t, xprev=x_prev)
            model_mean = x_prev
        elif self.mean_type == 'xstart':  # the model predicts x_0
            # print('xstart')
            x_0 = self.model(x_t, t)
            model_mean, _ = self.q_mean_variance(x_0, x_t, t)
        elif self.mean_type == 'epsilon':  # the model predicts epsilon
            # print('epsilon')
            eps = self.model(x_t, t)  # 模型预测的噪声
            x_0 = self.predict_xstart_from_eps(x_t, t, eps=eps)  # 得到均值计算需要的X0
            model_mean, _ = self.q_mean_variance(x_0, x_t, t)  # 计算均值
        else:
            raise NotImplementedError(self.mean_type)
        x_0 = torch.clip(x_0, -1., 1.)

        return model_mean, model_log_var

    def forward(self, x_T):
        """
        Algorithm 2.
        """
        x_t = x_T  # torch.Size([64, 3, 32, 32])
        # print('x_t', x_t.shape)
        for time_step in reversed(range(self.T)):
            t = x_t.new_ones([x_T.shape[0], ], dtype=torch.long) * time_step  # 时间步,torch.Size([64])
            # print('t.shape',t.shape)
            mean, log_var = self.p_mean_variance(x_t=x_t, t=t)
            # print('mean',mean)
            # print('log_var',log_var)
            # no noise when t == 0
            if time_step > 0:
                # print('have noise')
                noise = torch.randn_like(x_t)
            else:
                # print('not noise')
                noise = 0
            x_t = mean + torch.exp(0.5 * log_var) * noise  # 得到Xt-1，循环得到X0
            # print('x_t',x_t)
        x_0 = x_t
        return torch.clip(x_0, -1, 1)

forward()中
通过
在这里插入图片描述
生成时间步。
通过

计算均值和方差。具体为：

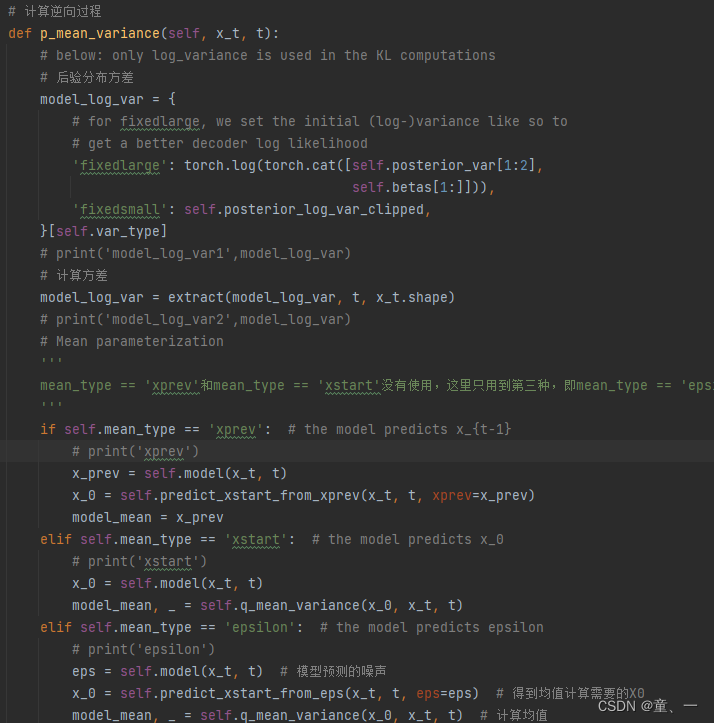
均值类型有‘xprev’、‘xstart’和‘epsilon’三种，这里只使用了‘epsilon’。
即通过

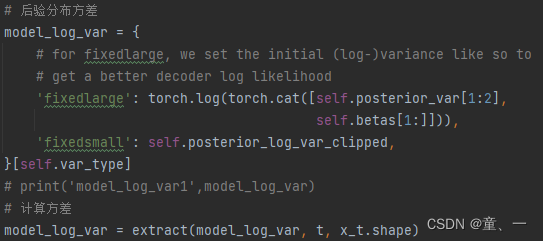
计算方差，由于方差是常数，因此可以直接得出。使用公式为：
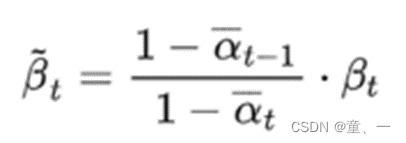
在这里插入图片描述

通过
在这里插入图片描述
计算均值。其中eps为trainer中训练好后预测输出的噪声。然后使用

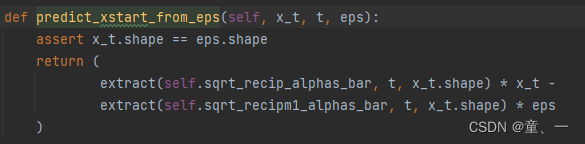
得出原图片X₀.使用公式为

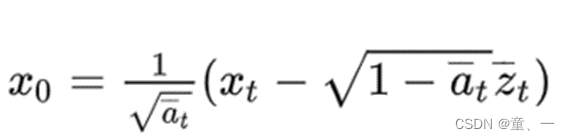
得出X₀后，使用

计算均值，具体为：

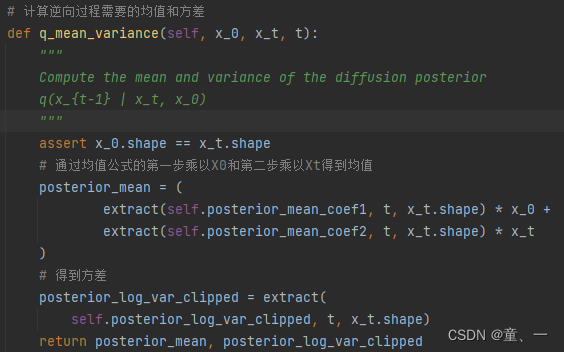
使用到的公式为

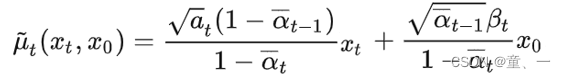
通过q_mean_variance()函数和p_mean_variance()计算得出均值和方差后，使用
在这里插入图片描述
计算X_t-1，使用的公式为

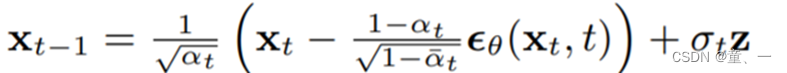
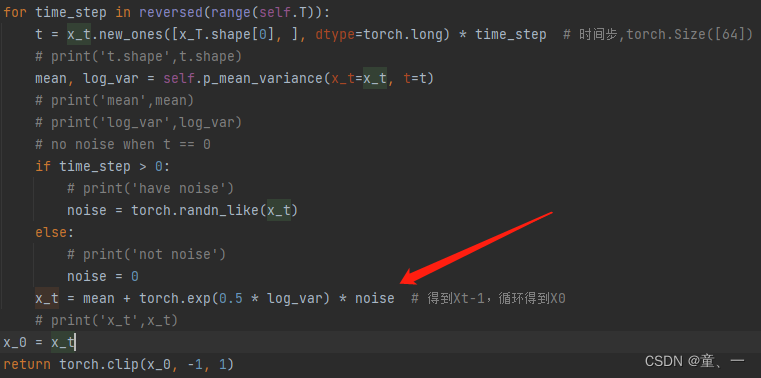
在这里插入图片描述
通过for循环将time_step从1000到0的过程就是从X_t到X₀的过程。
生成图像伪代码为：

二、Unet网络

Unet网络中分为DownBlocks、Middle和UpBlocks、tail
DownBlocks中一个Block包括两个ResBlock和一个DownSample，将Blocks重复三次再加上两个ResBlock后就构成了DonwBlocks。（特征提取作用）
MIddle由一个具有Attntion的ResBlock和一个普通的ResBlock组成。
UpBlocks中一个Block包括三个ResBlock和一个UpSample，将Blocks重复三次后再加上三个ResBlock就构成了UpBlocks。（特征融合作用）
tail由一个线性层+卷积层构成。
在这里插入图片描述

class UNet(nn.Module):
    def __init__(self, T, ch, ch_mult, attn, num_res_blocks, dropout):
        super().__init__()
        assert all([i < len(ch_mult) for i in attn]), 'attn index out of bound'
        tdim = ch * 4   #
        self.time_embedding = TimeEmbedding(T, ch, tdim)  # (1000,128,512)

        self.head = nn.Conv2d(3, ch, kernel_size=3, stride=1,
                              padding=1)  # (3,128,kernel_size(3,3),stride(1,1),padding(1,1))
        self.downblocks = nn.ModuleList()
        chs = [ch]  # record output channel when dowmsample for upsample
        now_ch = ch
        for i, mult in enumerate(ch_mult):
            out_ch = ch * mult
            for _ in range(num_res_blocks):
                self.downblocks.append(ResBlock(
                    in_ch=now_ch, out_ch=out_ch, tdim=tdim,
                    dropout=dropout, attn=(i in attn)))
                now_ch = out_ch
                chs.append(now_ch)
            if i != len(ch_mult) - 1:
                self.downblocks.append(DownSample(now_ch))
                chs.append(now_ch)

        self.middleblocks = nn.ModuleList([
            ResBlock(now_ch, now_ch, tdim, dropout, attn=True),
            ResBlock(now_ch, now_ch, tdim, dropout, attn=False),
        ])

        self.upblocks = nn.ModuleList()
        for i, mult in reversed(list(enumerate(ch_mult))):
            print('upblocks_i',i)
            print('upblocks_mult',mult)
            out_ch = ch * mult  # mult:2 2 2 1;out_ch = ch * mult =
            print('out_ch:',out_ch)
            for _ in range(num_res_blocks + 1):
                self.upblocks.append(ResBlock(
                    in_ch=chs.pop() + now_ch, out_ch=out_ch, tdim=tdim,
                    dropout=dropout, attn=(i in attn)))
                now_ch = out_ch
            if i != 0:
                self.upblocks.append(UpSample(now_ch))
        assert len(chs) == 0

        self.tail = nn.Sequential(
            nn.GroupNorm(32, now_ch),
            Swish(),
            nn.Conv2d(now_ch, 3, 3, stride=1, padding=1)
        )
        self.initialize()

    def initialize(self):
        init.xavier_uniform_(self.head.weight)
        init.zeros_(self.head.bias)
        init.xavier_uniform_(self.tail[-1].weight, gain=1e-5)
        init.zeros_(self.tail[-1].bias)

    def forward(self, x, t):
        # Timestep embedding
        # print('t.shape',t.shape)    # torch.Size([64])
        # print('x.shape', x.shape)   # torch.Size([64, 3, 32, 32])
        temb = self.time_embedding(t)  # (64,512)
        # print('temb',temb)
        # Downsampling
        h = self.head(x)  # (64,128,32,32)
        hs = [h]
        for layer in self.downblocks:
            h = layer(h, temb)
            hs.append(h)
        # Middle
        # print('h.shape',h.shape)    # torch.Size([64, 256, 4, 4]),尺寸从32x32变为4x4
        for layer in self.middleblocks:
            h = layer(h, temb)
        # print('h.shape', h.shape)  # torch.Size([64, 256, 4, 4])
        # Upsampling
        for layer in self.upblocks:
            if isinstance(layer, ResBlock):  # isinstance() 函数来判断一个对象是否是一个已知的类型
                h = torch.cat([h, hs.pop()], dim=1)
            h = layer(h, temb)
        # print('h.shape',h.shape)    # torch.Size([64, 128, 32, 32])
        h = self.tail(h)
        # print('h.shape', h.shape)   # torch.Size([64, 3, 32, 32])
        assert len(hs) == 0
        return h  # torch.Size([64, 3, 32, 32])

forward()中先使用TimeEmbedding()函数生成时间步。然后将输出的图(64,3,32,32)经过一个head()，即经过卷积改变通道数送入DownBlocks中，DownBlocks经过下采样将尺寸从32x32变为4x4，然后送入Middle，经过Middle处理后送入UpBlocks，UpBlock将尺寸从4x4上采样为32x32，通道数由256变为128，然后经过tail处理使图片通道数从128回到3，即最后返回的尺寸为(64,3,32,32)。