欢迎订阅《FPGA学习入门100例教程》、《MATLAB学习入门100例教程》
目录
一、理论基础
二、核心程序
三、测试结果
一、理论基础
土壤有机碳库是陆地生态系统中最丰富的碳库,其动态变化和存储分布在土壤质量评估、农田生态管理和气候变化适应与减缓等领域起着至关重要的作用。土壤有机碳储量的准确评估通常取决于土壤有机碳密度,其微小变化会显着影响大气中二氧化碳的浓度,从而进一步影响全球碳循环和生态平衡。因此对土壤有机碳密度进行精细预测对于更好的评估区域甚至全球土壤有机碳储量和理解生态系统碳循环至关重要。此外,土壤有机碳是景观中的三维实体,应更注意其垂直分布。其空间预测不仅应停留在表层,深层同样拥有大量的碳储量,且与评估总土壤有机碳储量相比,各层储量更为重要。表层土壤有机碳对地表径流、水分渗透、侵蚀控制和土壤耕作起着显著作用;而亚表层土壤碳动态比表层慢7倍。因此,更好地表述不同层土壤有机碳密度和储量的空间分布很有必要。此外,明确不同地表类型上土壤有机碳储量在不同土壤深度的差异,可以更好理解土壤有机碳的垂直分布,从而有助于理解深层碳如何转化为碳源或碳汇。
基于数字化土壤制图,结合多种环境信息可实现土壤有机碳相关属性的三维制图。研究人员通常拟合土壤有机碳密度与土壤深度的函数以实现土壤有机碳密度和储量的三维预测;此外,结合土壤深度作为协变量的地统计一步法模型也得到了广泛应用。然而,现有的土壤有机碳储量估算方法存在以下缺陷。第一,对于函数拟合方法来说,各层独立建模忽略了不同深度之间的关系及其相互作用;第二,建模过程中,若将不同的环境协变量应用于不同的深度区间,会使模型解释更加困难;第三,并非所有采样点都随深度遵循同一衰减模式,且任一层的属性值都会影响总体拟合效果;第四,对于使用土壤深度作为协变量的三维建模方法,存在不确定性较大、精度较低、无法生成现实预测的问题。因此,建立充分利用土壤深度信息,并考虑各层之间的非线性关系以及地表分类信息的融合方法,有助于解决上述问题,进一步提高土壤有机碳储量估算精度。
高精度曲面建模(highaccuracysurfacemodeling,hasm)方法是近年来发展起来的用于地理信息系统和生态建模的一种基于微分几何学曲面理论的曲面建模方法。
HASM原始的模型,其差分迭代公式如下所示:
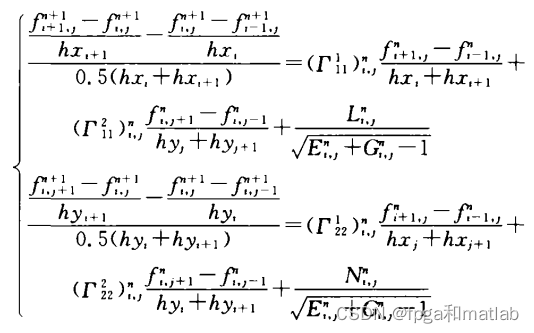
式中:
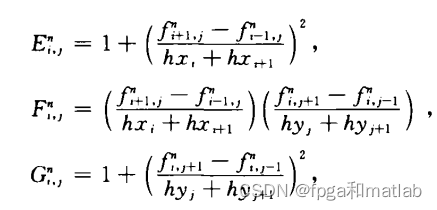
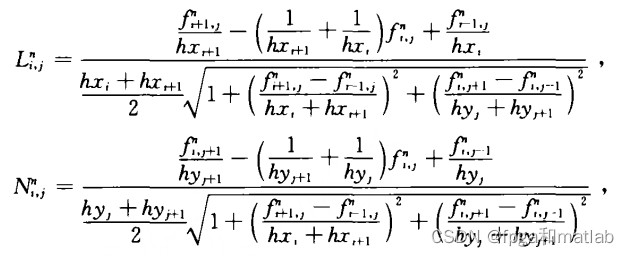
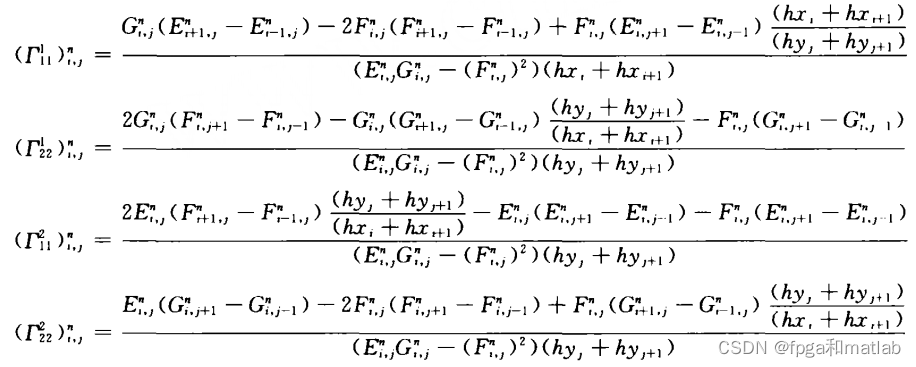
上面的公式非常复杂,会导致计算量非常大,且运算速度慢,所以,我们在实际中,会简化这个HASM模型,下面重点介绍我们是如何简化这个模型的。
·首先简化第一类参数:

这里设hxi = hyi = h,那么上面的式子可以等效为:

·然后简化第二类参数:
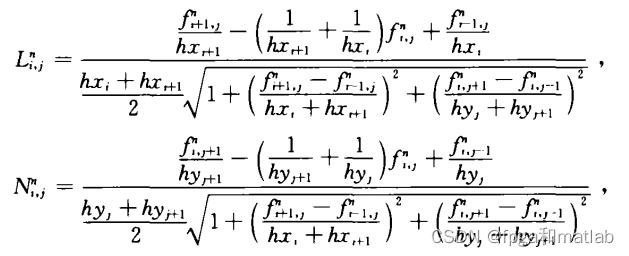
上面的式子,同样道理,可以简化为:
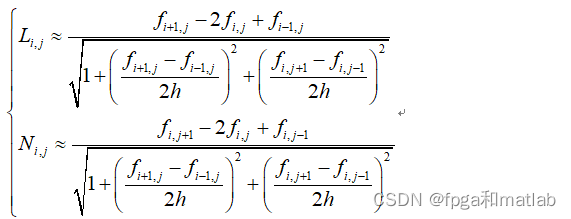
·最后简化第三类参数:
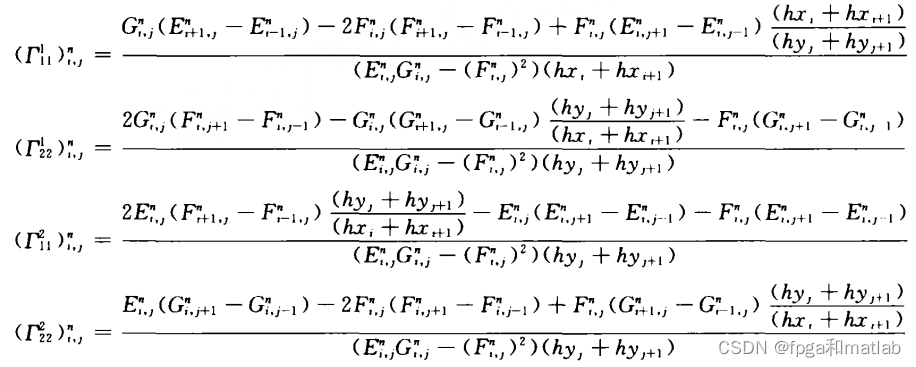
上面的式子,同样道理,可以简化为:
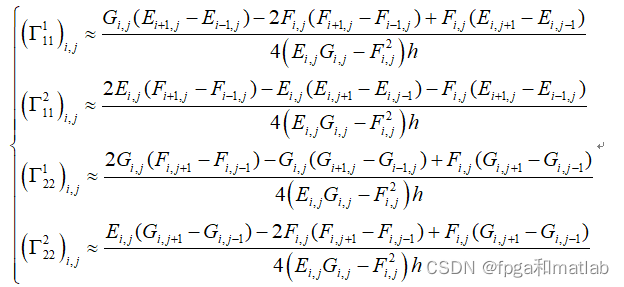
最后,我们得到的差分迭代公式为:
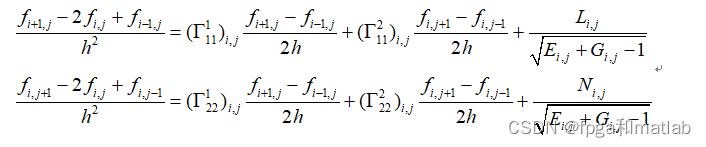
二、核心程序
clc;
clear;
close all;
warning off;
sel2 = 2; %1: 全采样,2:1/4的采样率,3:1/9的采样率,4:1/16的采样率.........
Interation = 10; %迭代次数
%调用数据文件
load datas.mat
%ncols 2268
%nrows 3105
%xllcorner 395510.20315996
%yllcorner 3279918.3520021
%cellsize 25
%NODATA_value -9999
%将数据中的NAN转换为-9999,因为-9999表示的是非数据
%下面的代码是将你原始数据中的NAN类型的数据转换为非值数据-9999
[r,c] = size(data);
for i = 1:r
for j = 1:c
if isnan(data(i,j)) == 1
data(i,j) = -9999;
end
end
end
%-9999不参与其中的运算,将其直接替换为0
for i = 1:r
for j = 1:c
if data(i,j) == -9999
data(i,j) = 0;
end
end
end
%由于原始的数据太大了,MATLAB会报错,内存不够,而且HASM的计算计算量非常巨大,所以需要降低原始数据的维度
%这个代码就是降维功能
data2 = func_samples(data,sel2);
clear data;
data = data2;
[r,c] = size(data);
%利用HASM进行曲面建模,并进行迭代从而逼近最后的真实值
%分辨率
h = 0.5;
alpha = 0.07;
%HASM建模结果变量
f = zeros(r,c,Interation);
%第一类基本变量
E = zeros(r,c);
F = zeros(r,c);
G = zeros(r,c);
%第二类基本变量
L = zeros(r,c);
N = zeros(r,c);
%第三类基本变量
T1_11 = zeros(r,c);
T1_22 = zeros(r,c);
T2_11 = zeros(r,c);
T2_22 = zeros(r,c);
%开始迭代循环
if Interation > 15
disp('There will be out of memory');
break;
else
for n = 1:Interation
disp('iteration ');
n
for i = 2:r-1
for j = 2:c-1
if n == 1
%以下就是HASM的迭代公式,具体的公式,将在设计说明中介绍
f(i,j,n) = data(i,j);
%第一类基本变量
E(i,j) = 1 + (( f(i,j+1,n) - f(i,j-1,n) )/( 2*h ))^2;
F(i,j) = (( f(i,j+1,n) - f(i,j-1,n) )/( 2*h )) * (( f(i+1,j,n) - f(i-1,j,n) )/( 2*h ));
G(i,j) = 1 + (( f(i,j+1,n) - f(i,j-1,n) )/( 2*h ))^2;
%第二类基本变量
L(i,j) = ( f(i+1,j,n) - 2*f(i,j,n) + f(i-1,j,n) )/(sqrt( 1 + (( f(i,j+1,n) - f(i,j-1,n) )/( 2*h ))^2 + (( f(i+1,j,n) - f(i-1,j,n) )/( 2*h ))^2));
N(i,j) = ( f(i,j+1,n) - 2*f(i,j,n) + f(i,j-1,n) )/(sqrt( 1 + (( f(i,j+1,n) - f(i,j-1,n) )/( 2*h ))^2 + (( f(i+1,j,n) - f(i-1,j,n) )/( 2*h ))^2));
%第三类基本变量
T1_11(i,j) = ( G(i,j) * ( E(i+1,j) - E(i-1,j) ) - 2*F(i,j)*( F(i+1,j) - F(i-1,j) ) + F(i,j)*( E(i,j+1) - E(i,j-1) ) )/( 4*( E(i,j)*G(i,j) - F(i,j)^2 )*h );
T2_11(i,j) =(2*E(i,j) * ( F(i+1,j) - F(i-1,j) ) - E(i,j)*( E(i,j+1) - E(i,j-1) ) - F(i,j)*( E(i+1,j) - E(i-1,j) ) )/( 4*( E(i,j)*G(i,j) - F(i,j)^2 )*h );
T1_22(i,j) =(2*G(i,j) * ( F(i,j+1) - F(i,j-1) ) - G(i,j)*( G(i+1,j) - G(i-1,j) ) - F(i,j)*( G(i,j+1) - G(i,j-1) ) )/( 4*( E(i,j)*G(i,j) - F(i,j)^2 )*h );
T2_22(i,j) =( E(i,j) * ( G(i,j+1) - G(i,j-1) ) - 2*F(i,j)*( F(i,j+1) - F(i,j-1) ) + F(i,j)*( G(i+1,j) - G(i-1,j) ) )/( 4*( E(i,j)*G(i,j) - F(i,j)^2 )*h );
end
if n >= 2
%以下就是HASM的迭代公式,具体的公式,将在设计说明中介绍
%第一类基本变量
E(i,j) = 1 + (( f(i,j+1,n-1) - f(i,j-1,n-1) )/( 2*h ))^2;
F(i,j) = (( f(i,j+1,n-1) - f(i,j-1,n-1) )/( 2*h )) * (( f(i+1,j,n-1) - f(i-1,j,n-1) )/( 2*h ));
G(i,j) = 1 + (( f(i,j+1,n-1) - f(i,j-1,n-1) )/( 2*h ))^2;
%第二类基本变量
L(i,j) = ( f(i+1,j,n-1) - 2*f(i,j,n-1) + f(i-1,j,n-1) )/(sqrt( 1 + (( f(i,j+1,n-1) - f(i,j-1,n-1) )/( 2*h ))^2 + (( f(i+1,j,n-1) - f(i-1,j,n-1) )/( 2*h ))^2));
N(i,j) = ( f(i,j+1,n-1) - 2*f(i,j,n-1) + f(i,j-1,n-1) )/(sqrt( 1 + (( f(i,j+1,n-1) - f(i,j-1,n-1) )/( 2*h ))^2 + (( f(i+1,j,n-1) - f(i-1,j,n-1) )/( 2*h ))^2));
%第三类基本变量
T1_11(i,j) = ( G(i,j) * ( E(i+1,j) - E(i-1,j) ) - 2*F(i,j)*( F(i+1,j) - F(i-1,j) ) + F(i,j)*( E(i,j+1) - E(i,j-1) ) )/( 4*( E(i,j)*G(i,j) - F(i,j)^2 )*h );
T2_11(i,j) =(2*E(i,j) * ( F(i+1,j) - F(i-1,j) ) - E(i,j)*( E(i,j+1) - E(i,j-1) ) - F(i,j)*( E(i+1,j) - E(i-1,j) ) )/( 4*( E(i,j)*G(i,j) - F(i,j)^2 )*h );
T1_22(i,j) =(2*G(i,j) * ( F(i,j+1) - F(i,j-1) ) - G(i,j)*( G(i+1,j) - G(i-1,j) ) - F(i,j)*( G(i,j+1) - G(i,j-1) ) )/( 4*( E(i,j)*G(i,j) - F(i,j)^2 )*h );
T2_22(i,j) =( E(i,j) * ( G(i,j+1) - G(i,j-1) ) - 2*F(i,j)*( F(i,j+1) - F(i,j-1) ) + F(i,j)*( G(i+1,j) - G(i-1,j) ) )/( 4*( E(i,j)*G(i,j) - F(i,j)^2 )*h );
%差分方程的迭代
%TMP1 = f(i+1,j,n) - 2*f(i,j,n) + f(i-1,j,n)
TMP1(i,j) = (h^2) * ( T1_11(i,j) * (f(i+1,j,n) - f(i-1,j,n))/(2*h) + T2_11(i,j) * (f(i,j+1,n) - f(i,j-1,n))/(2*h) + L(i,j)/(sqrt(E(i,j) + G(i,j) -1)) );
%删除异常点
if TMP1(i,j) > 8
TMP1(i,j) = 8;
end
if TMP1(i,j) < -6
TMP1(i,j) = -6;
end
%TMP2 = f(i,j+1,n) - 2*f(i,j,n) + f(i,j-1,n)
TMP2(i,j) = (h^2) * ( T1_22(i,j) * (f(i+1,j,n) - f(i-1,j,n))/(2*h) + T2_22(i,j) * (f(i,j+1,n) - f(i,j-1,n))/(2*h) + N(i,j)/(sqrt(E(i,j) + G(i,j) -1)) );
%删除异常点
if TMP2(i,j) > 8
TMP2(i,j) = 8;
end
if TMP2(i,j) < -6
TMP2(i,j) = -6;
end
%下面是上面的迭代结果,计算f(i,j,n)
%TMP1 = f(i+1,j,n) - 2*f(i,j,n) + f(i-1,j,n)
%TMP2 = f(i,j+1,n) - 2*f(i,j,n) + f(i,j-1,n)
f(i,j,n) = f(i,j,n-1) + alpha*(TMP1(i,j) - TMP2(i,j))/2;
end
end
end
end
end
figure;
Fmin = max(min(min(f(:,:,Interation))),0);
Fmax = max(max(f(:,:,Interation)))/3;
clims = [Fmin,Fmax];
data3 = f(:,:,Interation);
imagesc(data3,clims);
title('HASM迭代后的结果');
axis square;
%保存最后的计算结果
save result.mat data3
%将数据保存到txt文件中
fid = fopen('savedat.txt','wt');
for i = 1:r
for j = 1:c
fprintf(fid,'%d ',data3(i,j));
end
fprintf(fid,'\n');
end
fclose(fid);
三、测试结果

A16-16