1966A - Card Exchange
题意:
思路:手玩一下发现当存在某个数字个数超过k个,那么就能一直操作下去。那么答案就是k-1.
void solve()
{
cin >> n >> m;
map<int,int>mp;
int maxx = 1;
for(int i = 0 ; i < n ; i ++){
int x;
cin >> x;
mp[x]++;
maxx = max(maxx , mp[x]);
}
if(n < m){
cout << n <<endl;
}
else{
if(maxx >= m){
cout << m - 1 << endl;
}
else{
cout << n <<endl;
}
}
} 1966B - Rectangle Filling
题意: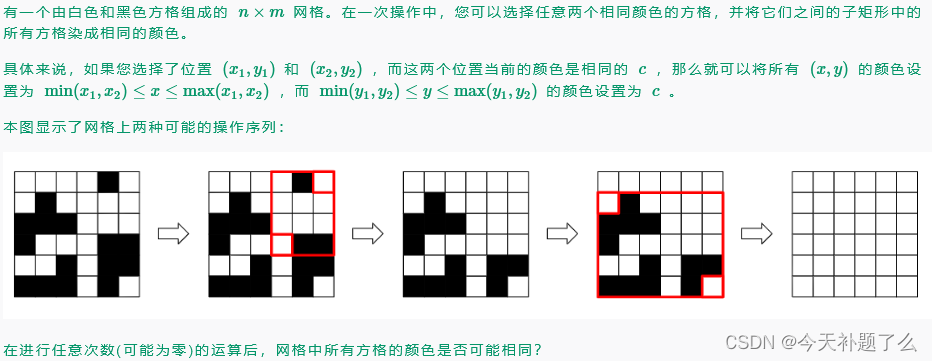
思路:若要使得所有方格同色,关键在于四个角上的颜色,若对角上的颜色一样就能直接将所有格子变为同色。因此本题变为能否使得对角上颜色相同,分类讨论
void solve()
{
cin >> n >> m;
int mp[n + 5][m + 5];
for(int i = 1 ; i <= n ; i ++){
string str;
cin >> str;
for(int j = 1 ; j <= m ; j ++){
if(str[j - 1] == 'W'){
mp[i][j] = 1;
}
else
mp[i][j] = 0;
}
}
if(n == 1){
if(mp[1][1] != mp[1][m]){
cout << "NO\n";
}
else{
cout<<"YES\n";
}
return;
}
if(m == 1){
if(mp[1][1] == mp[n][1]){
cout<<"YES\n";
}
else{
cout<<"NO\n";
}
return;
}
if(mp[1][1] == mp[n][m] || mp[1][m] == mp[n][1]){
cout<<"YES\n";
}
else{
if(mp[1][1] == mp[1][m]){
for(int i = 1 ; i <= m ; i ++){
if(mp[1][i] != mp[1][1]){
cout <<"YES\n";
return;
}
}
for(int i = 1 ; i <= m ; i ++){
if(mp[n][i] != mp[n][1]){
cout <<"YES\n";
return;
}
}
cout <<"NO\n";
}
else{
for(int i = 1 ; i <= n ; i ++){
if(mp[i][1] != mp[1][1]){
cout <<"YES\n";
return;
}
}
for(int i = 1 ; i <= n ; i ++){
if(mp[i][m] != mp[n][m]){
cout <<"YES\n";
return;
}
}
cout <<"NO\n";
}
}
} 1966C - Everything Nim
题意:
思路:为了方便考虑,我们令所有大小相同的堆为一个堆。接下来考虑终态:即只剩下一个堆。然后考虑若此时存在两个堆,那么对于Alice而言,其操作可以使得小的那个堆只剩下1,下一步Bob必须选1,然后Alice就胜利了。相反,若小的那个堆一开始就是1,那么Alice就输了。接下来推广到若干堆的情况:对于任意一方而言,若最小堆不是1,那么便可以控制胜利,于是我们只需要枚举到最小堆不是1的情况即可,然后看是谁在操作就是谁赢。
void solve()
{
cin >> n;
set<int>st;
for(int i = 1 ; i <= n ; i ++){
int x;
cin >> x;
st.insert(x);
}
vector<int>v;
for(auto it : st)
v.pb(it);
vector<int>tag;
int len = v.size();
int cnt = 1;
for(int i = 1 ; i < len ; i ++){
if(v[i] - v[i - 1] == 1){
cnt++;
}
else{
tag.pb(cnt);
cnt = 1;
}
}
tag.pb(cnt);
/* for(auto it : tag){
cout << it << endl;
}*/
if(tag.size() == 1){
if(v[0] == 1){
if(tag[0] & 1){
cout <<"Alice\n";
}
else{
cout<<"Bob\n";
}
}
else{
cout<<"Alice\n";
}
}
else{
if(v[0] == 1 && tag[0] % 2 == 1){
cout <<"Bob\n";
}
else
cout<<"Alice\n";
}
// cout << endl;
} 1966D - Missing Subsequence Sum
题意:
思路:首先处理 < k 的部分,我们可以通过二进制的思想来构造整数,例如可以用
来表示,其中36代表了99-63 .接下来考虑 > k 的部分,考虑到一个规律:
可以表示
的任何数,也就是说通过
再配合上前面的
就能表示出任意>k的数了,这就是构造方案。
void solve()
{
//1 ~ 99 101 201 301
//
vector<int>ans;
cin >> n >> m;
int st = 1;
int t = m;
if(m == 1){
ans.pb(2);
ans.pb(3);
ans.pb(4);
int st = 8;
for(int i = 3 ; i < 25 ; i ++){
ans.pb(st);
st *= 2;
}
cout << ans.size() << endl;
for(auto it : ans){
cout << it <<" ";
}
cout << endl;
return ;
}
while(st < t){
ans.pb(st);
t -= st;
st *= 2;
}
if(t - 1)
ans.pb(t - 1);
ans.pb(m + 1);
ans.pb(m * 2 + 1);
ans.pb(m * 3 + 1);
ans.pb(m * 4 + 1);
st = m * 8 + 1;
int len = ans.size();
for(int i = len + 1; i <= 25 ; i ++){
ans.pb(st);
st = st * 2 - 1;
}
cout << ans.size() << endl;
for(auto it : ans){
cout << it <<" ";
}
cout << endl;
}