paper：link
code：还没公开

摘要

  任意分割模型(SAM)是图像分割的基本框架。虽然它在典型场景中表现出显著的零镜头泛化，但当应用于医学图像和遥感等专门领域时，其优势就会减弱。针对这一局限性，本文提出了一种简单有效的参数高效微调方法Conv-Lora。通过将超轻量级卷积参数集成到低阶自适应(LORA)中，Conv-LoRa可以在普通VIT编码器中注入与图像相关的感应偏差，进一步强化了SAM的局部先验假设。值得注意的是，Conv-Lora不仅保留了SAM丰富的分割知识，而且恢复了其学习高层图像语义的能力，这一能力受到SAM前景-背景分割预训练的限制。跨多个领域的不同基准测试的全面实验强调了ConvLoRA在使SAM适应现实世界的语义分割任务方面的优势。

1.介绍

1）SAM的图像编码器是一种普通的VIT，众所周知，它缺乏视觉特定的感应偏差，这对密集预测有用。
2）SAM的预训练本质是一个二值掩膜预测任务，在给定一个指示的情况下，它将目标的前景和背景分离，低层掩码预测预训练阻碍了SAM捕获高层图像语义信息的能力，这些能力对于多类语义分割等任务至关重要。
  为了克服上述限制，同时仍然保留SAM在预训练期间获得有价值的分割知识，微调了一部分模型参数，同时冻结了SAM的大部分预先训练的权重，实现了参数高效微调（PEFT:parameter efficient finetuning )，从而提出一个问题：PEFT能否使用与图像相关的局部先验信息来增强SAM编码器，并促进高级语义信息的获取。
  在本文中，我们提出了一种新的PEFT方法，称为Conv-LORA，深入到低阶适应(LORA)(Hu等人，2021)。LORA将可训练的线性投影层引入SAM编码器的每一层变换器层，从而帮助恢复其提取高级语义信息的能力。我们的实验表明，LORA优于广泛采用的视觉提示调整(VPT)(Jia等人，2022)，特别是在多类语义切分任务中。在Lora之上，Conv-Lora在其瓶颈结构中集成了轻量级卷积层。卷积可以通过局部空间运算引入与图像相关的局部先验信息(即一个像素与其相邻像素的相关性比与距离较远的像素更强)(Chen等，2022)。此外，考虑到目标尺度的潜在变化，在适当的尺度(S)中注入局部先验是必要的。为此，Conv-Lora从专家混合(MoE)的概念中获得灵感(Shazeer等人，2017年)，并纳入了多个并行卷积专家，每个专家专门从事不同的特征规模。由于VIT以固定的比例处理图像特征，通常从原始分辨率向下采样16倍，Conv-Lora的每个专家最初以特定比例恢复图像特征，应用卷积运算，然后将特征恢复到默认比例。与VIT-Adaptor(Chen等人，2022)和Swin Transformer(Liu等人，2021A)等视觉特定转换器相比，Conv-Lora提供了一种隐式方法来实施多尺度局部先验，假设它可以利用默认尺度上的图像特征来重建更高尺度上的特征信息。幸运的是，SAM的监督预训练包括各种尺度的面具，使VIT能够获得超出默认尺度的图像特征知识。
  本着PEFT的精神，我们还去掉了提示编码器，并在掩码解码器中增加了轻量级的MLP，以实现多类预测。这一简单的修改将SAM转换为端到端模型，该模型可以在二进制和多类语义分割应用程序上进行微调。
总体而言，我们的贡献可以概括为：
1.我们提出了一种创新的PEFT技术Conv-Lora。通过加入辅助卷积运算，Conv-LoRa从处理普通VIT限制的角度加强了SAM的局部先验。
2.Conv-Lora使用MOE对动态选择适当的特征尺度以注入视觉特定的感应偏差的过程进行建模。
3.我们的研究表明，SAM的预训练阻碍了其VIT编码器学习高级图像语义信息的能力。然而，LoRA展示了帮助SAM恢复这一关键能力的潜力。
4.我们进行了一项涵盖多个领域的广泛基准，包括自然图像、农业、遥感和医疗保健。在各种下游任务中，Conv-Lora始终表现出优于其他PEFT技术的性能

2.模型结构图

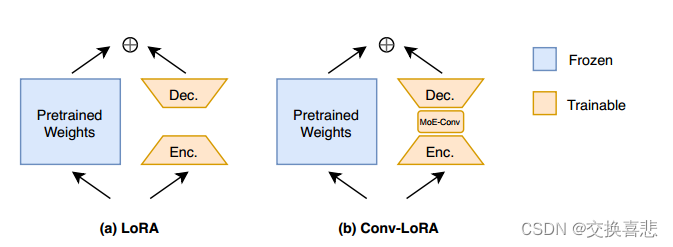
Conv-LoRA插入了由MoE管理的轻量级卷积运算，额外参数可以忽略不计 ；在我们的方法中，虽然MoE主要用于预训练，但我们将MOE用作下游任务的参数高效调整的一部分。

3.方法

3.1 CONV——LoRA

LoRA：首先，让我们简要地回顾一下LORA(Hu等人，2021年)的设计，它使用编码器-解码器结构来对权重更新施加低阶约束。它冻结预先训练的模型权重，并将小的可训练秩分解矩阵注入变压器体系结构的每一层。具体地，在给定预先训练的权重矩阵的情况下，LoRA在其一侧增加了一对线性编码器$W_e$和解码器$W_d$，即可训练的秩分解矩阵。$W_e$和$W_d$满足低阶约束$W_e\in R^{b\times a}$,
$W_d\in R^{b\times r}$和$r\le \min (a,b)$。
使用LoRA时，前向传播从$h=W_{0}x$更改为:
$$h=W_{0}x+W_d{W}_{e}x$$
Conv-LoRA:旨在结合LORA的编码器和解码器组件之间的卷积运算。一方面，卷积可以注入与图像相关的局部先验，解决了VIT的根本局限性。另一方面，低阶约束确保卷积层保持极轻，保持了Conv-Lora的PEFT性质.
  在设计Conv-Lora时，一个关键的考虑因素是确定引入局部先验的特征映射的比例。虽然VIT中的功能地图在比例上是一致的，但对象蒙版通常包含广泛的比例范围。因此，在适当的范围内应用卷积运算是至关重要的。为了应对这一挑战，我们从混合专家(MoE)的概念中获得灵感(Shazeer等人，2017年)。MOE包括多个专家网络和选通模块，该选通模块动态地选择在前向传球期间激活哪个专家(S)(图2)。3)。将这一概念应用于Conv-LoRa，每个专家专门在特定比例的特征地图上卷积，紧凑的门控模块学习根据输入数据动态选择expert。数学上，用Conv-Lora，将等式更改为：
$$h=W_{0}x+W_d(\sum _i^{n}G(W_{e}x{)}_i{E}_i(W_{e}x))$$
式子中$W_0\in R^{C_{out}\times C_{in}}$,$W_e\in R^{r\times C_{in}}$,$W_d\in R^{C_{out}\times r}$,$x\in R^{B\times C_{in}\times H\times W}$,B是批量大小，$C_{in}/C_{out}$为输入/输出通道数，H和W为对应高度和宽度。$E_i$是所有的n位expert中的第i为expert，G是仅激活top-k（默认为1）值的选通网络。
在每个expert内部，依次安排三个关键操作：重建特定比例尺的特征地图的内插函数、3×3卷积层，以及随后的将特征地图映射回VIT的默认特征比例尺的插补操作。假设expert $E_i$负责规模$S_i$，我们可以将其表示为：
$$E_i(x)=Interpolate(Con{v}_{3\times 3}(Interpolate(x,s_i),1/s_i)$$
例如，如果$s_i$等于4，则expert $E_i$最初会将特征映射放大4倍，应用$Con{v}_{3\times 3}$操作，最后将特征映射缩小4倍。

MoE vs.Multi-scale:与MoE不同的是，另一种应对不同规模的方法是采用多规模战略。该方法利用多个分支在不同的尺度上同时注入局部先验，并聚集结果。虽然这种方法看起来更简单，但与MoE相比，它的计算成本更高。MOE的效率源于其选择性地激活稀疏expert的能力，从而将计算开销降至最低。考虑到我们对高效微调的优先考虑，我们支持MoE作为一个有洞察力的选择。

3.2 END-TO-END MULTI-CALSS SEGMENTATION WITH SAM

基于SAM的端到端多类分割
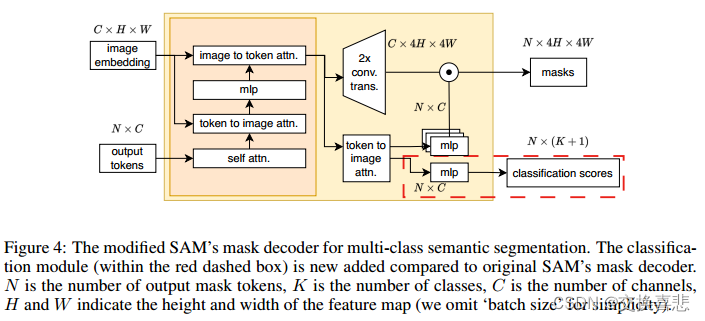
  SAM由三个基本组件组成：图像编码器、提示编码器和掩码解码器。当提供图像和提示时，掩码解码器生成与给定提示相关联的对象的掩码，所述图像和提示可以采取点、框、掩码或文本的形式。虽然这种基于提示的方法使SAM可以灵活地集成到更大的系统中，例如交互式分段或检测和后续分段的组合，但它在使SAM成为实际应用中的端到端模型方面确实存在挑战。为了自动化SAM，我们冻结了提示编码器，因此在对下游任务进行微调时，总是不断地使用提示令牌来屏蔽解码器。此外，原始掩码解码器被设计为预测二进制掩码，根据给定的提示区分前景和背景。为了使SAM适应多类语义分割任务，我们引入了一个简单的分类分支(在图中描绘为红色虚线框。4)在掩码解码器内。这个额外的分支负责预测分类分数。此外，我们对掩码解码器进行了全面的微调，因为它是一个轻量级的模块。

4.实验（experiments）

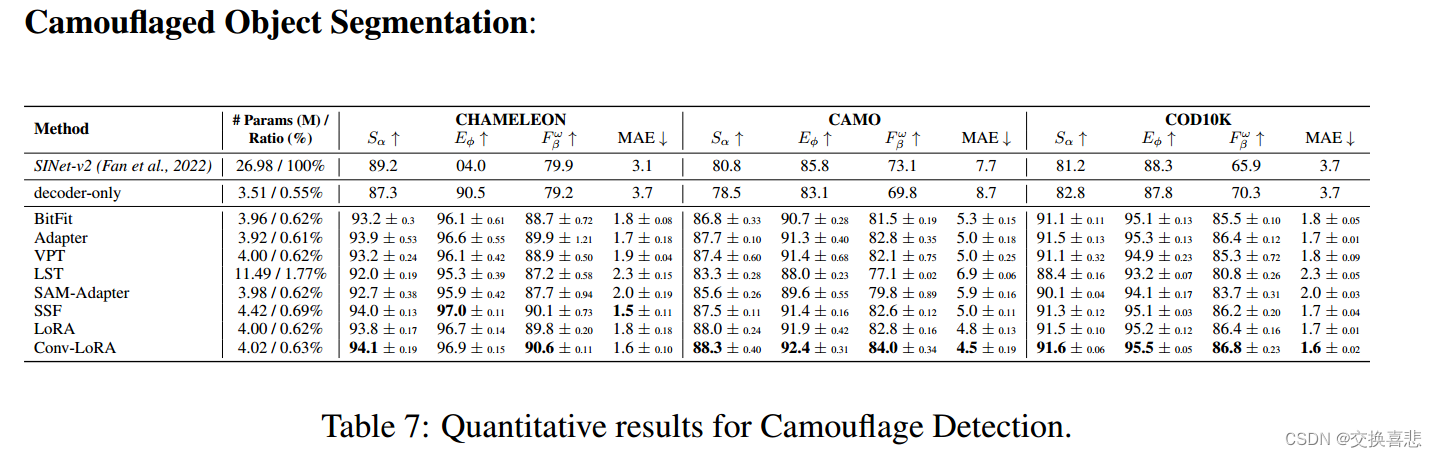
在COD任务上的表现：

5.结论

  参数高效微调(PEFT)是使基础模型适应各种下游任务时的一种流行方法。我们提出了一种新的将SAM应用于下游细分应用的PEFT方法Conv-LORA。Conv-LORA简单、通用，在自然图像、农业、遥感和医疗保健等多个领域取得了令人振奋的结果。此外，我们的研究还揭示了SAM的几个方面：1)虽然大规模监督分割预训练可以从数据的角度提供与图像相关的局部先验知识，但在VIT编码器中加入轻量级卷积运算可以从另一个体系结构的角度进一步促进对局部先验知识的开发；2)前景-背景分割预训练阻止图像编码器学习高层语义信息，这可以通过对编码器中相对较少的参数进行微调来缓解。我们的工作主要集中在为SAM开发通用的PEFT方法，在广泛的基准测试中显示出比现有PEFT方法更好的性能，而不是在专门领域与最先进的(SOTA)模型直接竞争。考虑到使用Conv-Lora微调的SAM可能还不能始终优于特定于域的SOTA模型，我们认为，在图像编码器微调的基础上定制掩码解码器和即时编码器，并将Conv-Lora与其他PEFT方法相结合可能是特定于域的应用的有前途的方向。