​​​​​​

• 背景知识

  • FIR滤波器的特性与优点

    • 可精确地实现线性相位响应（Linear phase response），无相位失真；

    • 总是稳定的，所有极点都位于原点

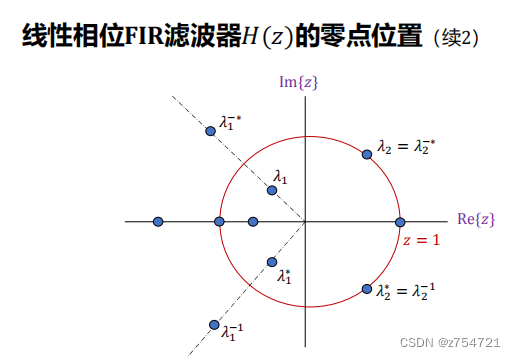
  • 线性相位FIR滤波器的性质、类型及零点位置

    • 冲击响应满足：奇或偶数长度、奇或偶对称

      • 1型，奇数长度 + 偶对称

      • 2型，偶数长度 + 偶对称

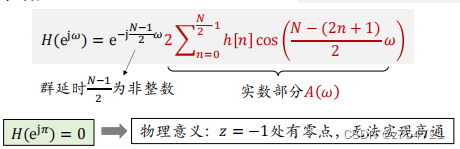
      • 3型，奇数长度 + 奇对称

      • 4型，偶数长度 + 奇对称

      • 

    • 零点位置（总结：一个零点，他的都是，他的共轭，他的倒数共轭也都是零点

      • 

      • 

      • 

• FIR滤波器的设计

  • 基于窗函数法的线性相位FIR滤波器设计

    • 其他固定窗

    • 窗函数法基本思想：对ℎ进行截短+移位，得到一个有限、长度、因果、线性相位的FIR滤波器。包含两个操作：

      • • 加窗截短：

      • 时间移位：

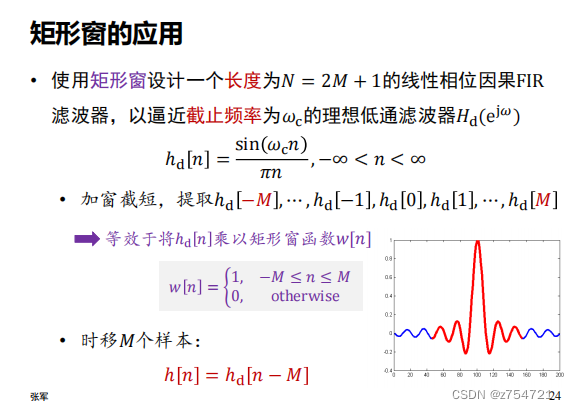
    • 矩形窗的应用及其分析

      • 例子：

      • 

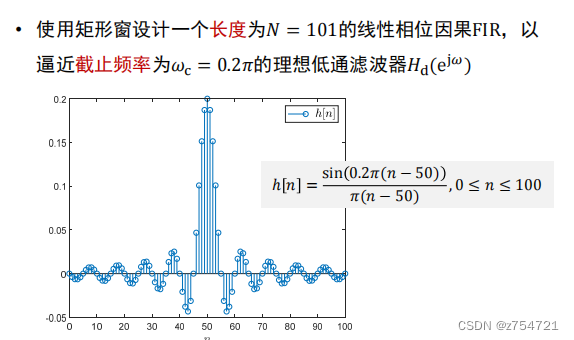
      • 低通滤波器，高于这个的频率被滤除

      • 分析：使用矩形窗得到的简单截短滤波器的幅度响应呈现振动的现象，通常称为“吉布斯现象

        • 吉布斯现象的原因：矩形窗函数中0与1之间的陡峭下降沿

        • 当N 增大，主瓣宽度及旁瓣宽度都减小，但最大波纹高度保持不变

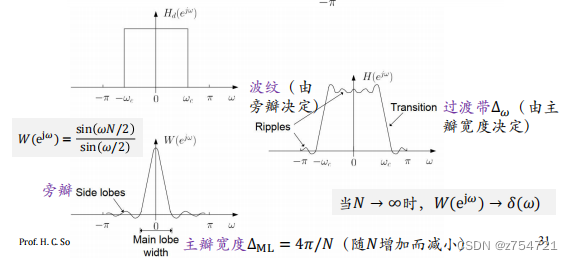
        • 如何消除？ • 使用逐渐平滑减小到零的窗函数 • 减小旁瓣高度，代价是增大主瓣宽度 和过渡带宽度Δw

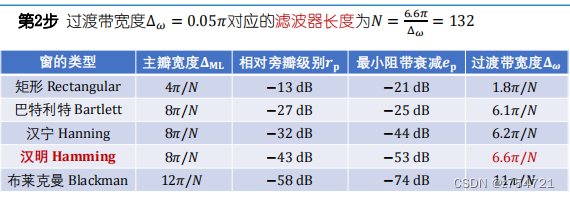
    • 不同窗函数的特性：

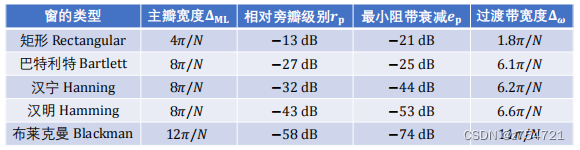
      • • 过渡带宽度 和波纹大小之间的折中 • 窗函数主瓣宽度决定了过渡带带宽，与窗类型、窗长有关 • 窗函数旁瓣高度决定了滤波器波纹，与窗类型有关，与窗长无关

      • 选择窗函数的标准：根据主板狂赌和过渡带要求选择滤波器长度；根据庞斑高度和波纹要求选择窗函数类型

  • FIR低通滤波器设计流程及案例

    • 基于固定窗函数的FIR低通滤波器设计流程

      • • 确定滤波器性能指标（过渡带宽度、波纹大小等）

      • • 根据所要求的旁瓣高度P d 或阻带衰减s d ，选择合适的窗类型

      • • 根据所要求的过渡带宽度Δ/ ，确定滤波器长度)

      • • 计算理想低通滤波器的冲激响应ℎX [ ]

      • • 加窗截短、右移，得到有限长因果低通FIR滤波器

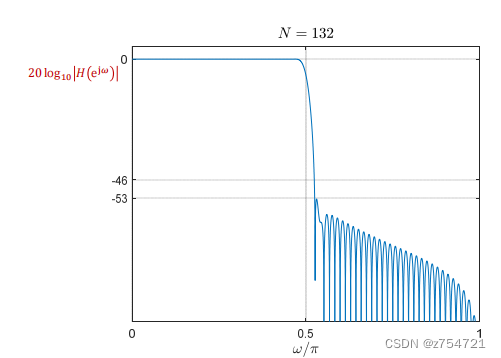
    • 基于固定窗函数的FIR低通滤波器设计案例

      • 

      • 

      • 

      • 

  • 拓展：FIR高通、带通、带阻滤波器

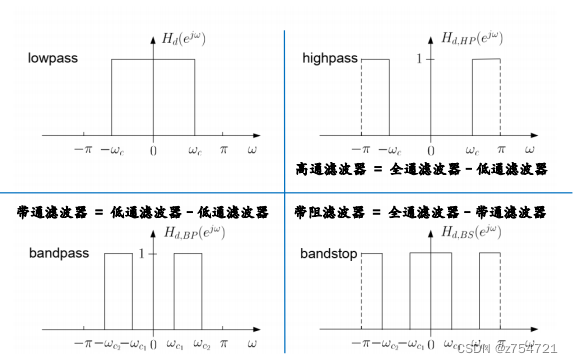
  • 其他设计方法

    • 可变窗函数法：增加一个参数，用来控制波纹大小：• 道尔夫-切比雪夫Dolph-Chebyshev窗，凯泽Kaiser窗

    • • 最优化等波纹线性相位FIR滤波器设计

    • • 频率抽样法