1. 解下列微分方程
   （1）y=dsolve(‘Dy=x+y’,‘y(0)=1’,‘x’)
   y =
   -x-1+2exp(x)
   x=[1 2 3]
   x = 1 2 3
   -x-1+2exp(x)
   ans =
   3.4366 11.7781 36.1711

（2）x’=2x+3y,y’=2x+y,x(0)=-2,y(0)=2.8,0<t<10,做相平面图
新建M函数
function dy=weifen1(t,y)
dy=zeros(2,1);
dy(1)=2y(1)+3y(2);
dy(2)=2y(1)+y(2);
输入命令
t=0:0.1:10;
[t,y]=ode15s(‘weifen1’,[0,10],[-2 2.8]);
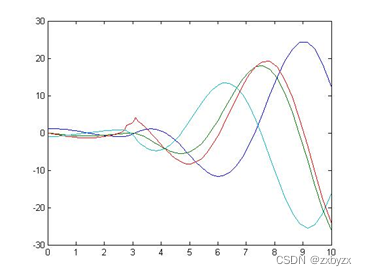
plot(t,y)

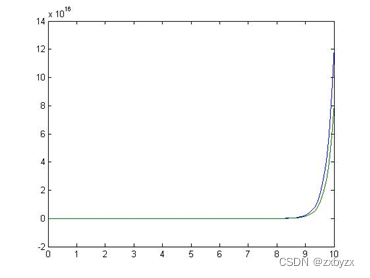
y’‘-0.01(y’)^2+2y1=sin(t),y(0)=0,y’(0)=1,0<t<5,做y的图
新建M函数
function dy=weifen2(t,y)
dy=zeros(2,1);
dy(1)=y(2);
dy(2)=0.01y(2)^2-2y(1)+sin(t);
输入命令
[t,y]=ode15s(‘weifen2’,[0,5],[0 1]);
plot(t,y)

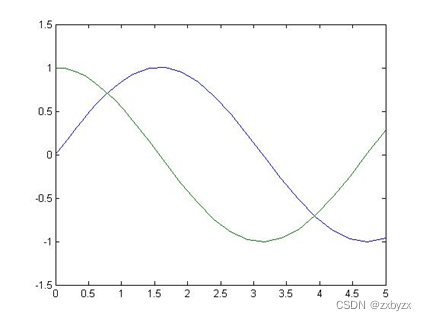
1.绘制飞船轨迹图
新建M函数
function dy=weifen3(t,y)
dy=zeros(4,1);
dy(1)=y(3);
dy(2)=y(4);
dy(3)=2y(4)+y(1)-(1-1/82.45)(y(1)+ 1/82.45)/((y(1)+1/82.45)^2+y(2)2)^{(3/2)-(1/82.45)*(y(1)+1/82.45-1)/((y(1)+1-1/82.45)}2+y(2)²⁾(3/2);
dy(4)=-2y(3)+y(2)-(1-1/82.45)*y(2)^{2/((y(1)+1/82.45)}2+y(2)²⁾(3/2)-(1/82.45)*y(2)/((y(1)+1-1/82.45)^2+y(2)2)^(3/2);
输入命令
[t,y]=ode15s(‘weifen3’,[0,10],[1.2 0 0 -1]);
plot(t,y)