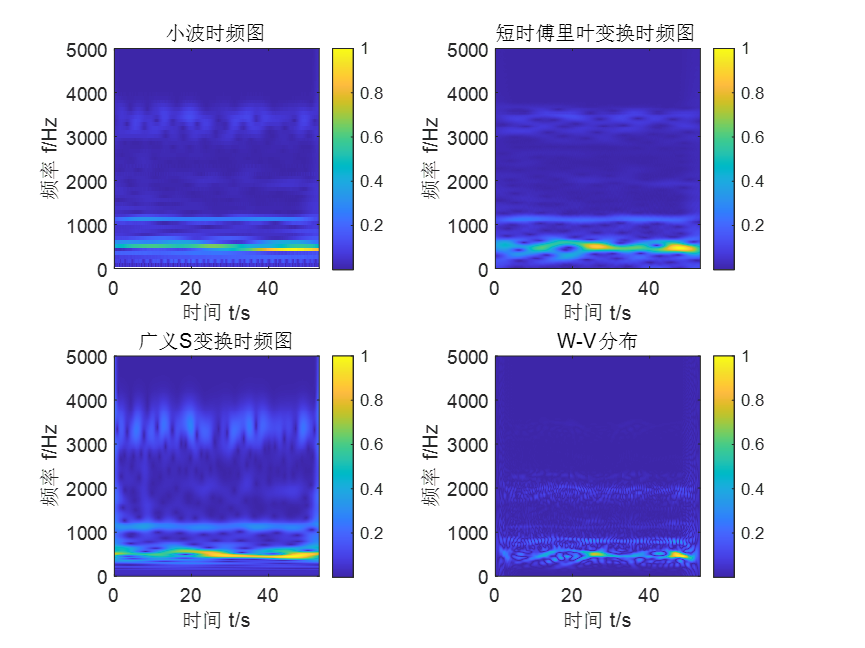
1.概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
int[] array ={5,3,4,1,7,8,2,6,0,9};
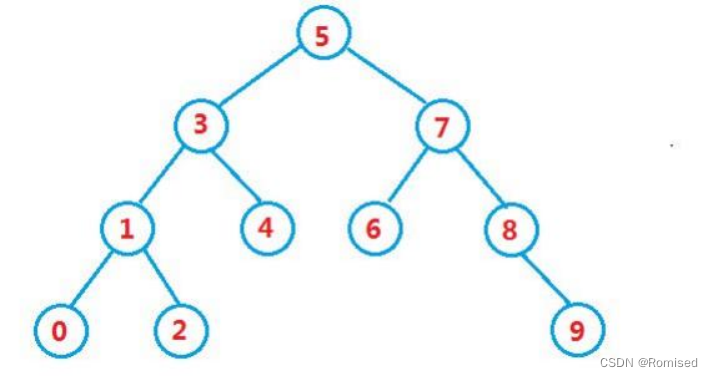
2.操作-查找
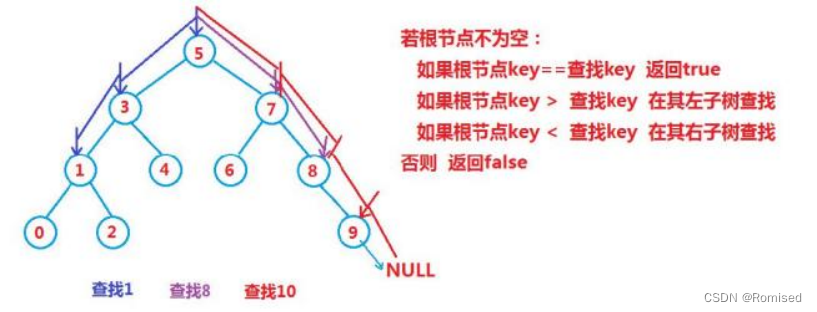
2.1实现
结点定义与实现
public class BinarySearchTree {
public static class Node {
int key;
Node left;
Node right;
public Node(int key) {
this.key = key;
}
}
private Node root = null;
//在搜索树中查找 key ,如果找到 ,返回 key 所在的结点 ,否则返回 null
public Node search(int key) {
Node cur = root;
while (cur != null) {
if (key == cur.key) {
return cur;
} else if (key < cur.key) {
cur = cur.left;
} else {
cur = cur.right;
}
}
return null;
}
}
3.操作-插入
1. 如果树为空树,即根 == null,直接插入

2. 如果树不是空树,按照查找逻辑确定插入位置,插入新结点
parent记录cur的上一个结点!
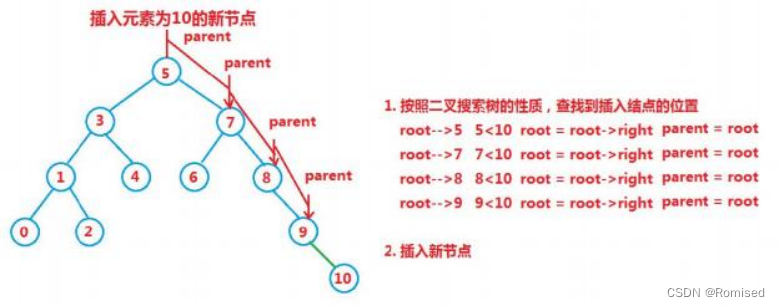
3.1插入实现
public boolean insert(int key) {
if (root == null) {
root = new Node(key);
return true;
}
Node cur = root;
Node parent = null;
while (cur != null) {
//不能有一样的key
if (key == cur.key) {
return false;
} else if (key < cur.key) {
parent = cur;
cur = cur.left;
} else {
parent = cur;
cur = cur.right;
}
}
Node node = new Node(key);
if (key < parent.key) {
parent.left = node;
} else {
parent.right = node;
}
return true;
}4.操作-删除(难点)
设待删除结点为 cur, 待删除结点的双亲结点为 parent
1. cur.left == null
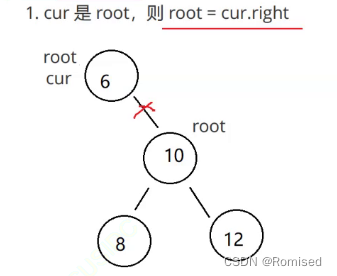
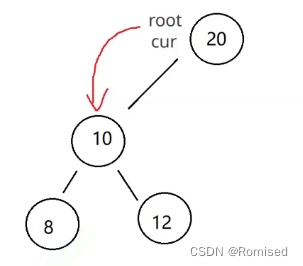
2. cur.right == null
1. cur 是 root,则 root = cur.left
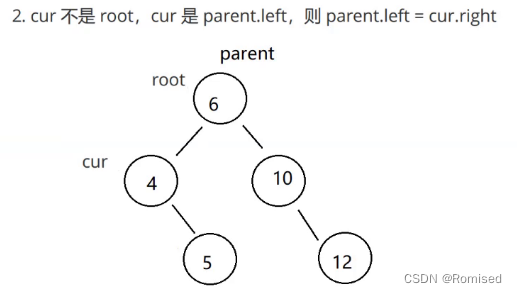
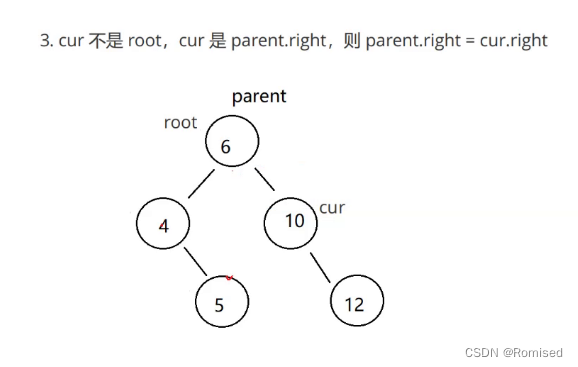
2. cur 不是 root ,cur 是 parent.left,则 parent.left = cur.left
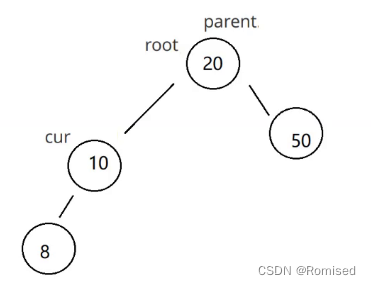
3. cur 不是 root ,cur 是 parent.right,则 parent.right = cur.left
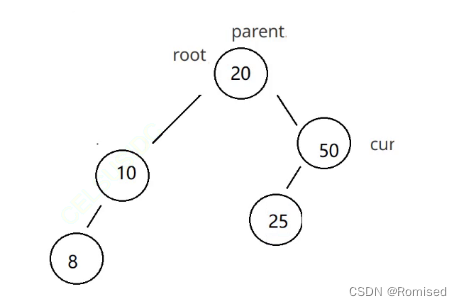
3. cur.left != null && cur.right != null
需要使用替换法进行删除,即在它的右子树中寻找中序下的第一个结点 (关键码最小),用它的值填补到被删除结点中,再来处理该结点的删除问题
例如需要删除结点10
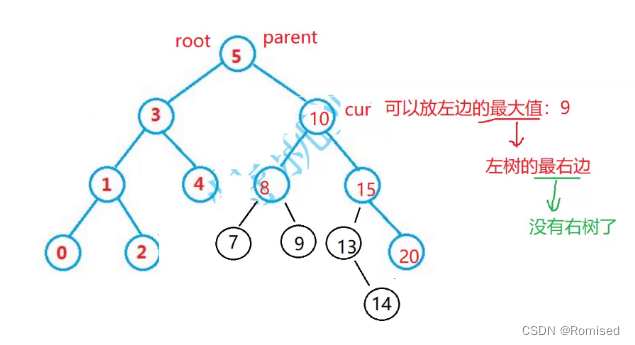
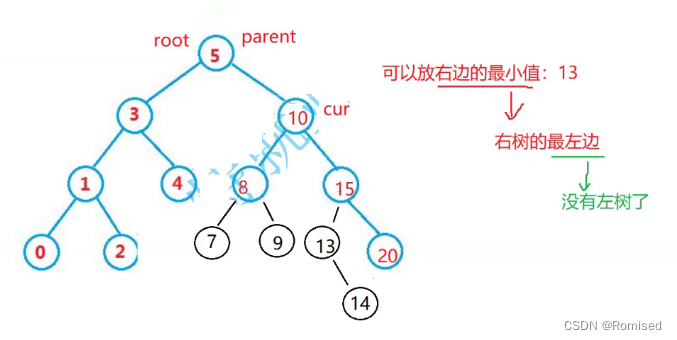
以右边为例,将右边的最小值13覆盖cur,因为13是最小值所以没有左树,因此可以按上面左树为空进行删除。
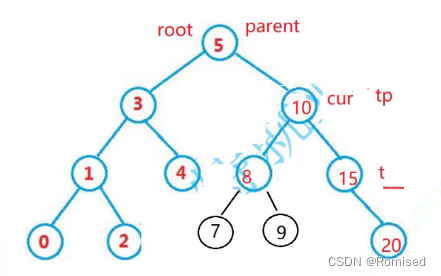
还要多判断一次t和tp的关系(特殊情况)
如果t = tp.right 则tp.right = t.right
4.1删除实现
public void removeNode(int key) {
TreeNode cur = root;
TreeNode parent = null;
while (cur != null) {
if(cur.val < key) {
parent = cur;
cur = cur.right;
}else if(cur.val > key) {
parent = cur;
cur = cur.left;
}else {
remove(cur,parent);
return;
}
}
}
/**
* 删除cur这个节点
* @param cur 要删除的节点
* @param parent 要删除的节点的父节点
*/
private void remove(TreeNode cur, TreeNode parent) {
if(cur.left == null) {
if(cur == root) {
root = cur.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if(cur.right == null) {
if(cur == root) {
root = cur.left;
}else if(parent.left == cur) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}else {
//cur的左右两边 都不为空 !!
TreeNode targetParent = cur;
TreeNode target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(target == targetParent.left) {
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}
}
}5.性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度 的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
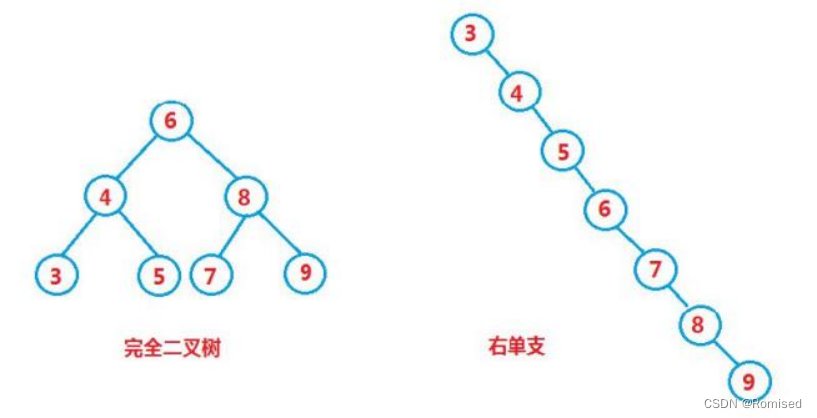
最优情况下,二叉搜索树为完全二叉树,其平均比较次数为: log2N
最差情况下,二叉搜索树退化为单支树,其平均比较次数为: N/2