上一篇我们学习的二叉树的理论，知道了什么是二叉树之后，我们来实现一棵二叉树，二叉树经常考的是前中后序的遍历，这里我们多实现一些功能。

---

1.二叉树功能

二叉树的实现充分利用了分治思想

1.前序遍历

2.中序遍历

3.后序遍历

4.树的最大深度

5.统计树的节点数

6.求树的叶子节点的个数

7.打印这几个叶子结点

8.二叉树查找值为x的节点

9.二叉树第k层节点个数

10.判断这棵二叉树是不是平衡二叉树

2.代码实现

Tree.h文件

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

typedef char AdataType;
//创建二叉树结构体
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	AdataType data;
}BTNode;
//初始化这棵树
void TreeInit(BTNode* root);
//创建树节点
BTNode* TreeNode(BTNode* root, AdataType x);
//前序遍历
void PrevOrder(BTNode* root);
//中序遍历
void InOrder(BTNode* root);
//后序遍历
void PostOrder(BTNode* root);
//统计这棵树共有几个节点
int TreeSize(BTNode* root);
//销毁树
void Destory2Tree(BTNode* root);
//求一棵树的叶子节点的个数
int TreeLeafSize(BTNode* root);
//求这几个叶子节点
void TreeLeafNode(BTNode* root);
//求这个树的最大深度
int TreeDepth(BTNode* root);
// 二叉树第k层节点个数
int TreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, AdataType x);
//判断这棵树是不是平衡二叉树
bool IsBalanced(BTNode* root);

Tree.c文件

#include"Tree.h"
//初始化这棵树
void TreeInit(BTNode* root)
{
	root->left = root->right = NULL;
	root->data = 0;
}

//创建树节点
BTNode* TreeNode(BTNode* root, AdataType x)
{
	/*assert(root);*/
	root = (BTNode*)malloc(sizeof(BTNode));
	if (root == NULL)
	{
		perror("malloc");
		exit(-1);
	}
	root->data = x;
	root->left = root->right = NULL;
	return root;
}

//前序遍历
void PrevOrder(BTNode* root)
{
	//这里不能断言，当root为空的时候，说明它是空树，是空二叉树
	//assert(root);
	if (root == NULL)
	{
		printf(" NULL ");
		return;
	}
	printf(" %c ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);

}
//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf(" NULL ");

		return;
	}
	PrevOrder(root->left);
	printf(" %c ", root->data);
	PrevOrder(root->right);
}
//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf(" NULL ");
		return;
	}
	PrevOrder(root->left);
	PrevOrder(root->right);
	printf(" %c ", root->data);
}
//统计这棵树共有几个节点
int TreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//销毁树采用后序遍历
void Destory2Tree(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	Destory2Tree(root->left);
	Destory2Tree(root->right);
	free(root);
	root = NULL;
}
//求一棵树的叶子节点的个数
int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if ((root->left == NULL) && (root->right == NULL))
	{
		return 1;
	}
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

//求这几个叶子节点
void TreeLeafNode(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	if ((root->left == NULL) && (root->right == NULL))
	{
		printf(" %c ", root->data);
	}
	else
	{
		TreeLeafNode(root->left);
		TreeLeafNode(root->right);
	}
}
//求这个树的最大深度
int TreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int left = TreeDepth(root->left) + 1;
	int right = TreeDepth(root->right) + 1;
	return left > right ? left : right;

}

// 二叉树第k层节点个数
int TreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, AdataType x)
{
	//递归的结束条件:
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	//单边查找:先左后右
	if (BinaryTreeFind(root->left, x))//如果左边为空则向右查找
	{
		return BinaryTreeFind(root->left, x); //不为空则向下递归查找
	}
	else
	{
		return BinaryTreeFind(root->right, x);
	}
}
//判断这棵树是不是平衡二叉树
bool IsBalanced(BTNode* root)
{
	if (root == NULL)//若是空树，也满足平衡二叉树
	{
		return true;
	}
	int leftDepth = TreeDepth(root->left);
	int rightDepth = TreeDepth(root->right);
	return abs(leftDepth - rightDepth) < 2 && IsBalanced(root->left)
		&& IsBalanced(root->right);
}

test.c文件

#include"Tree.h"

void Test1()
{
	BTNode root;
	//意义不大，但还是写了一个
	TreeInit(&root);
	BTNode* A = TreeNode(&root, 'A');
	BTNode* B = TreeNode(&root, 'B');
	BTNode* C = TreeNode(&root, 'C');
	BTNode* D = TreeNode(&root, 'D');
	BTNode* E = TreeNode(&root, 'E');
	BTNode* F = TreeNode(&root, 'F');
	BTNode* G = TreeNode(&root, 'G');
	BTNode* H = TreeNode(&root, 'H');

	//关联成为一棵树
	A->left = B;
	A->right = C;
	B->left = D;
	B->right = E;
	E->right = H;
	C->left = F;
	C->right = G;
	printf(" PrevOrder:> ");
	PrevOrder(A);
	printf("\n");
	printf(" InOrder:>   ");
	InOrder(A);
	printf("\n");
	printf(" PostOrder:> ");
	PostOrder(A);
	printf("\n");

	int Depth = TreeDepth(A);
	printf(" Depth=%d \n", Depth);
	int Size = TreeSize(A);
	printf(" Size=%d \n", Size);
	printf(" TreeLeafNode:> ");
	TreeLeafNode(A);
	printf("\n");
	int KSize = TreeLevelKSize(A, 3);
	printf(" KSize=%d \n", KSize);
	BTNode* find = BinaryTreeFind(A, 'H');
	printf("查找到了 %c \n", find->data);

	printf(" IsBalanced>: ");
	if (IsBalanced(A))
	{
		printf(" the tree is balance tree!\n");
	}
	else
	{
		printf(" the tree is not balance tree!\n");
	}
	Destory2Tree(A);
	printf("树已销毁\n");
}

int main()
{
	Test1();
	return 0;
}

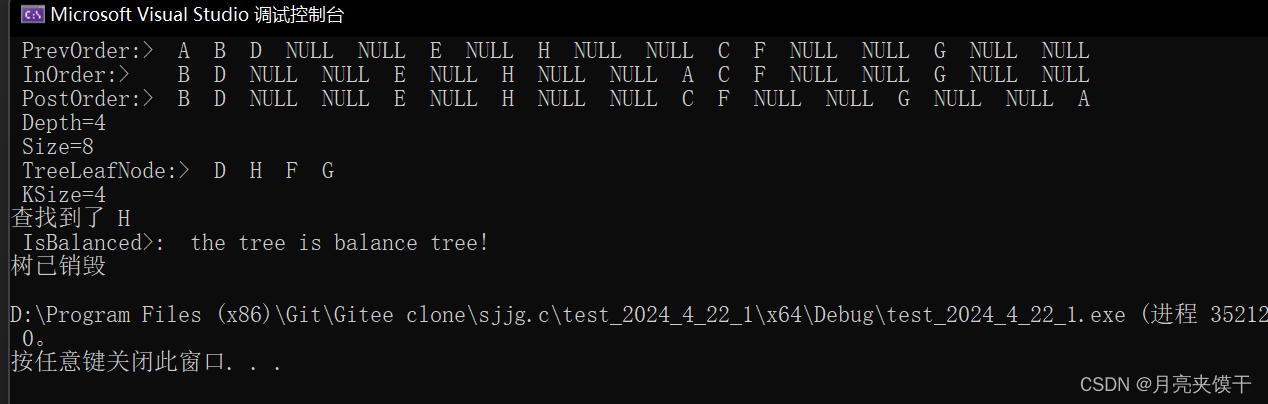
结果：

---

铁汁们快去试试吧，下期见！！！